2006年数学中考试卷及答案
数 学 试 卷(北师大)
(时间:120分钟 , 满分:150分)
| 题 号 | 一 | 二 | 三 | 总 分 | |||||||||
| (1~10) | (11~15) | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | ||
| 得 分 | |||||||||||||
| 评卷人 | |||||||||||||
一、精心选一选(本大题共10小题,每题3分,共30分. 在每题所给出的四个选项中,只有一项是符合题意的. 把所选项前的字母代号填在括号内. 相信你一定会选对!)
1、函数![]() 中自变量x的取值范围是( )
中自变量x的取值范围是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、某物体的三视图如下,那么该物体形状可能是( )
 |
A、长方体 B、圆锥体 C、立方体 D、圆柱体
3、下列图形中,既是轴对称,又是中心对称图形的是( )
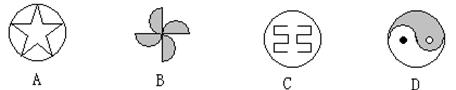
 4、如图1,天平右盘中的每个砝码的质量都是1g,则物体A的质量m(g)的取值范围,在数轴上可表示为( )
4、如图1,天平右盘中的每个砝码的质量都是1g,则物体A的质量m(g)的取值范围,在数轴上可表示为( )
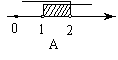
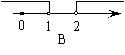
 |  | ||
5、把分式方程![]() 的两边同时乘以(x-2), 约去分母,得( )
的两边同时乘以(x-2), 约去分母,得( )
A.1-(1-x)=1 B.1+(1-x)=1
C.1-(1-x)=x-2 D.1+(1-x)=x-2
6、在一副52张扑克牌中(没有大小王)任意抽取一张牌,抽出的这张牌是方块的机会是( )
A、![]() B、
B、![]() C、
C、![]() D、0
D、0
7.将函数![]() 进行配方正确的结果应为( )
进行配方正确的结果应为( )
A ![]() B
B
![]()
C ![]() D
D
![]()
8、一个形式如圆锥的冰淇淋纸筒,其底面直径为![]() ,母线长为
,母线长为![]() ,围成这样的冰淇淋纸筒所需纸片的面积是
( )
,围成这样的冰淇淋纸筒所需纸片的面积是
( )
A、 ![]() B、
B、 ![]() C、
C、 ![]() D、
D、 ![]()
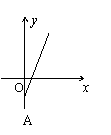
9、某村的粮食总产量为a(a为常量)吨,设该村粮食的人均产量为y(吨),人口数为x,则y与x之间的函数图象应为图中的( )
 |  | 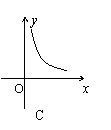 |  | ||||
 10、在圆环形路上有均匀分布的四家工厂甲、乙、丙、丁,每家工厂都有足够的仓库供产品储存. 现要将所有产品集中到一家工厂的仓库储存,已知甲、乙、丙、丁四家工厂的产量之比为1∶2∶3∶5. 若运费与路程、运的数量成正比例,为使选定的工厂仓库储存所有产品时总的运费最省,应选的工厂是( )
10、在圆环形路上有均匀分布的四家工厂甲、乙、丙、丁,每家工厂都有足够的仓库供产品储存. 现要将所有产品集中到一家工厂的仓库储存,已知甲、乙、丙、丁四家工厂的产量之比为1∶2∶3∶5. 若运费与路程、运的数量成正比例,为使选定的工厂仓库储存所有产品时总的运费最省,应选的工厂是( )
A、甲 B、乙 C、丙 D、丁
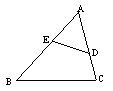 二、细心填一填(本大题共有5小题,每空4分,共20分.)
二、细心填一填(本大题共有5小题,每空4分,共20分.)
11、分解因式:3x2-12y2= .
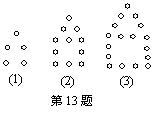 12.如图9,D、E分别是△ABC的边AC、AB上的点,请你添加一个条件,使△ADE与△ABC相似.你添加的条件是 .
12.如图9,D、E分别是△ABC的边AC、AB上的点,请你添加一个条件,使△ADE与△ABC相似.你添加的条件是 .
13.如下图所示,摆第一个“小屋子”要5枚棋子,
摆第二个要11枚棋子,摆第三个要17枚棋子,则摆
第30个“小屋子”要 枚棋子
14、如图是2005年6月份的日历,如图中那样,用一个圈竖着圈住3个数.如果被圈的三个数的和为39,则这三个数中最大的一个为 .
| 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 |
| 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
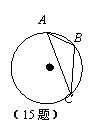 15.如图,在⊙O中,弦AB=1.8cm,圆周角∠ACB=30°,则⊙O的直径为__________cm.
15.如图,在⊙O中,弦AB=1.8cm,圆周角∠ACB=30°,则⊙O的直径为__________cm.
三、认真答一答(本大题共10小题,满分100分. 只要你认真思考, 仔细运算, 一定会解答正确的!)
16、(本题满分8分)计算:解方程组:![]()
17.(本题满分8分) (3)先将![]() 化简,然后请自选一个你喜欢的x值,再求原式的值.
化简,然后请自选一个你喜欢的x值,再求原式的值.
18.(本题满分8分) 在如图的方格纸中(每个小方格的边长都是1个单位)有一点O和△ABC.
(1)请以点O为位似中心,把△ABC缩小为原来的一半(不改变方向),得到△A′B′C′.
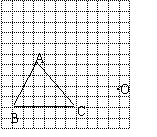 |
(2)请用适当的方式描述△A′B′C′的顶点A′、B′、C′的位置.
19.(本题满分10分)  (1)如图,在□ABCD中,对角线AC、BD相交于点O. 请找出图中的一对全等三角形,并给予证明.
(1)如图,在□ABCD中,对角线AC、BD相交于点O. 请找出图中的一对全等三角形,并给予证明.
 20(本小题满分10分)
20(本小题满分10分)
在某旅游景区上山的一条小路上,有一些断断续续的台阶.图11是其中的甲、乙段台阶路的示意图.请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
(1)两段台阶路有哪些相同点和不同点?
(2)哪段台阶路走起来更舒服?为什么?
(3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不娈的情况下,请你提出合理的整修建议.
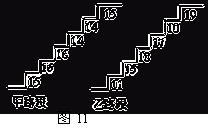 |
21.(本题满分10分)某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克. 经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6000元,同时又要顾客得到实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
22.(本题满分10分)小明和小亮进行百米赛跑,小明比小亮跑得快,如果两人同时起跑,小明肯定赢,现在小明让小亮先跑若干米,两人的路程![]() (米)分别与小明追赶时间
(米)分别与小明追赶时间![]() (秒)的函数关系如图所示。
(秒)的函数关系如图所示。
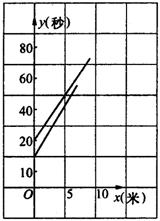 ⑴小明让小亮先跑了多少米?
⑴小明让小亮先跑了多少米?
⑵分别求出表示小明、小亮的路程与时间的函数关系式。
⑶谁将赢得这场比赛?请说明理由。
23.(12分)用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合,使三角尺的60°角的顶点与点A重合,两边分别与AB,AC重合.将三角尺绕点A按逆时针方向旋转.
(1)当三角尺的两边分别与菱形的两边BC,CD相交于点E,F时,(如图13—1),通过观察或测量BE,CF的长度,你能得出什么结论?并证明你的结论;
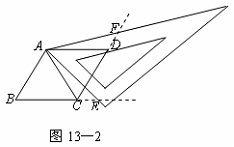
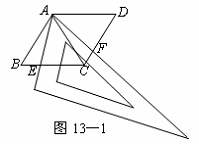 (2)当三角尺的两边分别与菱形的两边BC,CD的延长线相交于点E,F时(如图13—2),你在(1)中得到的结论还成立吗?简要说明理由.
(2)当三角尺的两边分别与菱形的两边BC,CD的延长线相交于点E,F时(如图13—2),你在(1)中得到的结论还成立吗?简要说明理由.
24(本题满分12分)、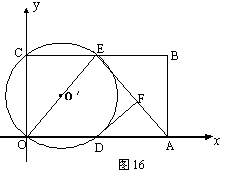 如图16,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2.E为BC的中点,以OE为直径的⊙O′交
如图16,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2.E为BC的中点,以OE为直径的⊙O′交![]() 轴于D点,过点D作DF⊥AE于点F.
轴于D点,过点D作DF⊥AE于点F.
(1) (4分) 求OA、OC的长;
解:
(2) (4分) 求证:DF为⊙O′的切线;
证明:
(3) (4分) 小明在解答本题时,发现△AOE是等腰三角形.由此,他断定:“直线BC上一定存在除点E以外的点P,使△AOP也是等腰三角形,且点P一定在⊙O′外”.你同意他的看法吗?请充分说明理由.
解:
25(本题满分12分)、已知抛物线y=x2+(2n-1)x+n2-1 (n为常数).
(1)当该抛物线经过坐标原点,并且顶点在第四象限时,求出它所对应的函数关系式;
(2)设A是(1)所确定的抛物线上位于x轴下方、且在对称轴左侧的一个动点,过A作x轴的平行线,交抛物线于另一点D,再作AB⊥x轴于B,DC⊥x轴于C.
①当BC=1时,求矩形ABCD的周长;
②试问矩形ABCD的周长是否存在最大值?如果存在,请求出这个最大值,并指出此时A点的坐标;如果不存在,请说明理由.
数学试卷答案
一:1、C;2、D;3、A;4、A;5、B;6、B;7、C;8、D;9、C;10、D。
二:11 、3(x-2y)(x+2y); 12、答案不唯一,如∠AED=∠ACB; 13、179; 14、20; 15、3.6 。
三:
16. ![]() ………………8分
………………8分
 17. 化简得x+2,……4分
17. 化简得x+2,……4分
例如取x=2(不能取1和0),得结果为4.……8分
18. (1)如图所示.……4分
(2)可建立坐标系用坐标来描述;也可说成点A′、B′、 C′的位置分别为OA、OB、OC的中点等. ……8分
19. 例:△AOB≌△COD. ……2分
证明:∵四边形ABCD为平行四边形,
∴OA=OC,OB=OD, ……6分
又∵∠AOB=∠COD,
∴△AOB≌△COD. ……10分
20. (1)![]()
![]()
∴相同点:两段台阶路高度的平均数相同. ……………………………………4分
不同点:两段台阶路高度的中位数、方差和极差均不相同. ………………6分
(2)甲路段走起来更舒服一些,因为它的台阶高度的方差小. ……………………8分
(3)每个台阶高度均为15cm(原平均数),使得方差为0. ……………………10分
21.(1)设每千克应涨价x元,则(10+x)(500-20x)=6000 ……4分
解得x=5或x=10,
为了使顾客得到实惠,所以x=5. ……6分
(2)设涨价x元时总利润为y,
则y=(10+x)(500-20x)= -20x2+300x+5000=-20(x-7.5) 2+6125
当x=7.5时,y取得最大值,最大值为6125. ……8分
答:(1)要保证每天盈利6000元,同时又使顾客得到实惠,那么每千克应涨价5元; (2)若该商场单纯从经济角度看,每千克这种水果涨价7.5元,能使商场获利最多.
……10分
22、⑴小明让小亮先跑5米 ……2分
⑵小明:![]() 经过(
经过(![]() ,
,![]() ),
),![]() ,
,
∴![]() ,
,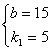 。
。
∴ ![]() ……4分
……4分
小亮:![]() 经过(
经过(![]() ,
,![]() ),(
),(![]() ,
,![]() ),
),
![]() ,
,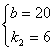
∴![]() ……8分
……8分
⑶小明百米赛跑: ![]() 小亮赢得这场比赛。 ……10分
小亮赢得这场比赛。 ……10分
23.(1)BE=CF. …………………………………………………………………2分
证明:在△ABE和△ACF中, ∵∠BAE+∠EAC=∠CAF+∠EAC=60°,
∴∠BAE=∠CAF.
∵AB=AC,∠B=∠ACF=60°,∴△ABE≌△ACF(ASA). ………………4分
∴BE=CF. ………………………………………………………………………6分
(2)BE=CF仍然成立. 根据三角形全等的判定公理,同样可以证明△ABE和△ACF全等,BE和CF是它们的对应边.所以BE=CF仍然成立.………………………………10分
说明:对于(2),如果学生仍按照(1)中的证明格式书写,同样可得本段满分.
24、解: (1)在矩形OABC中,设OC=x 则OA= x+2,依题意得
![]() 解得:
解得:![]()
![]() (不合题意,舍去) ∴OC=3, OA=5
… (4分)
(不合题意,舍去) ∴OC=3, OA=5
… (4分)
(只要学生写出OC=3,OA=5即给2分)
(2)连结O′D 在矩形OABC中,OC=AB,∠OCB=∠ABC=90![]() ,CE=BE=
,CE=BE=![]()
∴ △OCE≌△ABE ∴EA=EO ∴∠1=∠2
在⊙O′中, ∵ O′O= O′D ∴∠1=∠3
∴∠3=∠2 ∴O′D∥AE,
∵DF⊥AE ∴ DF⊥O′D
又∵点D在⊙O′上,O′D为⊙O′的半径 ,
∴DF为⊙O′切线。 … (8分)
(3) 不同意. 理由如下:
25 当AO=AP时,
以点A为圆心,以AO为半径画弧交BC于P1和P4两点
过P1点作P1H⊥OA于点H,P1H = OC = 3,∵A P1= OA = 5
∴A H = 4, ∴OH =1 求得点P1(1,3) 同理可得:P4(9,3) …… (9分)
②当OA=OP时,
同上可求得::P2(4,3),P3(![]() 4,3) …… (11分)
4,3) …… (11分)
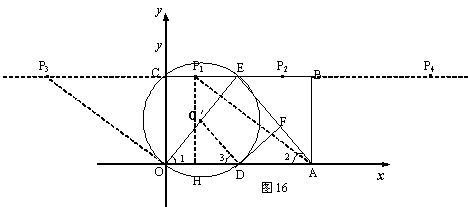 |
因此,在直线BC上,除了E点外,既存在⊙O′内的点P1,又存在⊙O′外的点P2、P3、P4,它们分别使△AOP为等腰三角形。 …… (12分)
25、解:(1)由已知条件,得:n2-1=0
解这个方程,得: n1=1 ,n2=-1;
当n=1时,得y=x2+x,此抛物线的顶点不在第四象限;
当n=-1时,得y=x2-3x,此抛物线的顶点在第四象限;
∴所求的函数关系式为y=x2-3x …… (4分)
(2)由y=x2-3x,令y=0,得x2-3x=0,解得x1=0 ,x2=3;
∴抛物线与x 轴的另一个交点为(3,0)
∴它的顶点为(![]() ),对称轴为直线x=
),对称轴为直线x=![]()
①∵BC=1,由抛物线和矩形的对称性易知OB=![]()
∴B(1,0)
∴点A的横坐标x=1,又点A在抛物线y=x2-3x上,
∴点A的纵坐标y=12-3×1=-2。
∴AB=y =2
∴矩形ABCD的周长为:2(AB+BC)=6 …… (8分)
②∵点A在抛物线y=x2-3x上,可以设A点的坐标为(x,x2-3x),
∴B点的坐标为 (x,0)。(0<x<![]()
∴BC=3-2x,A在x 轴的下方,
∴x2-3x<0
∴AB= x2-3x =3x-x2
∴矩形ABCD的周长P=2〔(3x-x2)+(3—2x)〕=-2(x-![]() )2+
)2+![]()
∵a=-2<0
∴当x=![]() 时, 矩形ABCD的周长P最大值是
时, 矩形ABCD的周长P最大值是![]() 。 …… (12分)
。 …… (12分)
其它解法,请参照评分建议酌情给分。