初三物理浮力（一）
一、浮力的概念
1.浮力的产生原因：由于浸在液体里的物体上下底面的深度不同，所受液体的压强不同，下底面向上的压强大于上底面向下的压强，从而使物体受到向上的压力大于向下的压力，这两个压力差就是浮力。
2.浮力的方向：总是竖直向上的。
3.显然，当物体浸在液体中，且底面与容器底部密接的时候，物体底部不再受到液体向上的压强时，它就不受浮力。比如，建筑在水中的桥墩；再比如，陷在泥中的物体。同学们都有这样的体会，在泥泞的水中走路时，有时，鞋会被泥“吸”住而被拽下来，就是因为鞋受到大气压和水向下的压强，而没有受到向上的浮力。
4.阿基米德定律：浸在液体里的物体受到向上的浮力，浮力的大小等于物体排开液体的重力。它不仅适用于液体也适用于气体。
公式：F浮=ρ液gV排
5.物体的浮沉条件：这是指物体只受浮力和重力而没有其他力作用的情况而言：浸在液体中的物体，如果受到的浮力大于它的重力，物体就上浮；如果浮力小于重力，物体就下沉；如果浮力等于重力，物体就可以停留在液体里任何深度的地方。
物体上浮、下沉、悬浮和漂浮的物理过程分析：物体全部浸入液体中所受浮力最大。当F浮>G物，则物体上浮，一直到露出液面瞬间仍是如此。当物体继续上升时，F浮减小，直到最后物体静止地漂浮于液面时，F浮=G物，此时F浮与G物是一对平衡力。若F浮<G物，物体下沉，一直到底，此时物体所受F浮虽不变，但增加一个容器底的支持力，在三力作用下物体处于平衡状态。当物体在液体内部某处满足F浮=G物的条件，物体将静止在液体里某处，这种现象叫悬浮。
根据浮沉现象可分析ρ物与ρ液的关系：当物体全部浸入液体时：ρ物<ρ液 则上浮；ρ物>ρ液时下沉；ρ物=ρ液则悬浮。比如把一块泡沫塑料按在水里，因为ρ塑<ρ水，一松手，塑料块将上浮。石块的密度比水大，把石块投入水中，会下沉。人体的平均密度大约与水相当，当人完全没入水中时，会悬浮，可以游潜泳。鱼类则是靠着鱼膘的鼓与瘪来调整鱼的体积，进而改变鱼的平均密度，使它可以上浮或下沉。
二、浮力大小的计算
浮力大小的计算可归纳为三种方法：
(1)求物体上下表面的压力差
F浮=F向上-F向下
(2)通过测量，从受力情况入手，由平衡条件推算出F浮=G-G′。其中G为物体在空气中的重力，G′为物体浸入液体中的视重（此时从弹簧测力计上显示的物重）。
(3)应用阿基米德定律
F浮=ρ液gV排
值得注意的是：应用以上方法计算浮力，要具体情况具体分析，首先要弄清每个公式的适用条件，物理意义，不可死背乱套。
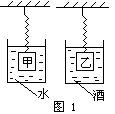
| 例题1：如图1所示，甲乙两个体积相等的实心球吊在弹簧测力计下，分别浸在水和酒精中静止。已知ρ甲=3ρ水，ρ乙=3ρ酒，ρ水>ρ酒。比较两个弹簧测力计示数的大小，下列判断正确的是（ ） |
|
分析与解答：依据关系式 F浮=G-G′可以变形为G′=G-F浮，此G′为物体的视重也就是弹簧测力计的示数。G甲=ρ甲gV甲，
，就有G甲′=ρ甲gV甲-ρ水gV甲=（3ρ水-ρ水）gV甲=2ρ水gV甲 。
同理可知G乙′=G乙-F浮乙=ρ乙gV乙-ρ酒gV乙
=（3ρ酒-ρ酒）gV乙=2ρ酒gV乙
∵V甲=V乙 ∴G甲′=2ρ水gV，G乙′=2ρ酒gV。
又∵ρ水>ρ酒 ∴G甲′>G乙′ 选A。
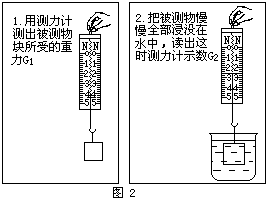
| 例题2 只用一个弹簧测力计和一杯水，怎样测定一块合金的密度？ 分析与解答 我们只要按照图乙所示的方法，读出两种情况下测力计G1与G2，就可以计算出物体的密度了。 |
|
由阿基米德定理：F浮=G排水，且物体浸没时V排=V物，∴G1-G2=ρ水gV物
（1） 又∵G1=m物g，
（2）
式（2）除以（1）得
。
这是一个巧妙的方法，本来求密度是离不开测物体体积的，这里通过浮力的计算代替掉了，只用弹簧秤和水就可以了。既不用天平也不用量筒就可以求物体密度了。
三、物体所受浮力的分析方法
浮力是物体所受到的各种力的一种，因此研究浮力对物体的作用，必须遵从力的一般分析方法，即首先要确定研究对象，对所选对象进行全面的受力分析，然后找出各物理量之间的数学关系再动手计算，求出所要求的量。
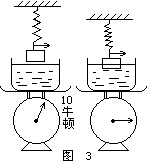
例题3 盘秤上放一盛水容器，秤的示数为10牛顿。将一5牛顿的物体吊在弹簧秤下放入水中，如图3所示，求当弹簧秤示数为4牛时，容器下的盘秤示数为多少？
分析：物、水、秤连在一起互相之间有相互作用力，必须分开研究。对于每一部分作全面受力分析，列出平衡力的关系，才能计算出容器下盘秤的示数。如图4所示，F浮与
分别是水对物的浮力与物对水的反作用力，N与N′分别是秤对水的支持力与水对秤的反作用力。（盛水容器与秤看成一体）
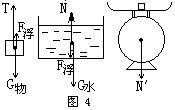
解：T+F浮=G物 N=+G水
F浮= N=N′
∵T=4牛，G物=5牛
∴F浮=G物-T=5牛-4牛=1牛
∵G水=10牛 =F浮=1牛
∴N′=N=1牛+10牛=11牛
即容器下的盘秤的示数是11牛顿。
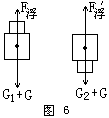
例题4 某物体漂浮于水中，如图5所示，将密度为5克/厘米3体积为V1的金属块放在该物上，整个物体刚好浸没在水中，若将体积为V2的同种金属块挂在该物体下也可以使其刚好浸没入水中，求V1与V2之比为多少？
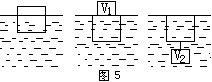
| 分析：根据题所给条件，物体与小金属块共同在重力和浮力作用下处于平衡状态，因此应选物体与金属块一起作为研究对象。如图6所示。 解：令物体体积为V，密度为ρ物，所受重力G： |
|
ρ金gV1=(ρ水-ρ物)gV
(ρ金-ρ水)gV2=(ρ水-ρ物)gV
∴ρ金gV1=(ρ金-ρ水)gV2
四、抓住本质，举一反三
应用浮力研究的问题是很多的，要善于抓住相同物理本质的题目，把它们抽象成同样的模型，这样才能举一反三，做一个题会一个题。
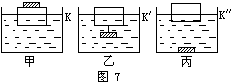
例题5 槽中水面上浮有一个木块，木块上压着一个铁块，如图7-甲所示，此时槽内水面位置在K处，若将铁块用细线系于木块下放入水中，如图7-乙所示，水面将如何变化？若将铁块取下放入水槽中沉入水底，如图7-丙所示，水面如何变化？
分析：如甲图所示木块与铁块浮于水面，F浮=G木+G铁，乙图所示相同的物理过程，只是铁块在下，木块在上，仍F浮=G木+G铁，所以水面不会变化。丙图所示则不然，当把铁块投入水中时，浮于水面的仅剩木块，浮力减小，水面会下降。
解：F浮1=ρ水gV排1=G木+G铁
F浮2=ρ水gV排2=G铁+G木
∴V排1=V排2，K=K′
F浮3=ρ水gV排3=G木<G木+G铁=ρ水gv排
∴V排3<V排1，
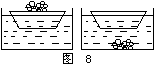
| 例题6 漂浮在水池中的小船上载有一些石块，若将石块抛于水中沉入池底，池中水面上升还是下降？（见图8） |
|
分析：可把小船与石块简化成木块与铁块的模型，从图9中很容易得出湖面会下降的结论。
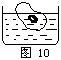
| 例题7 如图10所示，杯中浮在水面上的是一块含铅粒的冰块，若冰熔解后，杯中水面如何变化？ |
|
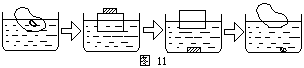
分析：如图11
所示冰块与其中的铅粒可简化成木块与铁块的模型，自然很快会得出杯中水面下降的结论。
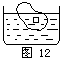
| 例题8如图12 所示，杯中水面浮一块含木块的冰，若冰熔解后，杯中水面如何变化？ |
|
分析：如图13
所示，冰与其中的木块可简化成木块与铁块的模型。
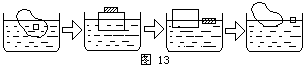
因为冰中木块的密度小于水的密度，所以木块不能沉于水底，水对冰及木块的浮力不变，因此液面保持不变。
同样若冰中所含是蜡块等密度小于水的杂质，都是同样的物理本质，结论应同样是液面保持不变。