2004年全国高考数学试题汇编——解析几何(一)
1.[2004年全国高考(山东山西河南河北江西安徽)·理科数学第7题,文科数学第7题]
椭圆![]() 的两个焦点为F1、F2,过F1作垂直于x轴的直线与椭圆相交,一个交点为P,则
的两个焦点为F1、F2,过F1作垂直于x轴的直线与椭圆相交,一个交点为P,则![]() = ( )
= ( )
A.![]() B.
B.![]() C.
C.![]() D.4
D.4
2.[2004年全国高考(山东山西河南河北江西安徽)·理科数学第8题,文科数学第8题]
设抛物线y2=8x的准线与x轴交于点Q,若过点Q的直线l与抛物线有公共点,则直线l的斜率的取值范围是 ( )
A.[-![]() ,
,![]() ] B.[-2,2] C.[-1,1] D.[-4,4]
] B.[-2,2] C.[-1,1] D.[-4,4]
3.[2004年全国高考(山东山西河南河北江西安徽)·理科数学第14题,文科数学第15题]
由动点P向圆x2+y2=1引两条切线PA、PB,切点分别为A、B,∠APB=60°,则动点P的轨迹方程为 .
4.[2004年全国高考(四川云南吉林黑龙江)· 理科数学第4题,文科数学第4题]
已知圆C与圆![]() 关于直线
关于直线![]() 对称,则圆C的方程为 ( )
对称,则圆C的方程为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.[2004年全国高考(四川云南吉林黑龙江)· 文科数学第8题]
已知点A(1,2)、B(3,1),则线段AB的垂直平分线的方程是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.[2004年全国高考(四川云南吉林黑龙江)· 理科数学第8题]
在坐标平面内,与点A(1,2)距离为1,且与点B(3,1)距离为2的直线共有 ( )
A.1条 B.2条 C.3条 D.4条
7.[2004年全国高考(四川云南吉林黑龙江)· 理科数学第9题]
已知平面上直线l的方向向量e=![]() 点O(0,0)和A(1,-2)在l上的射影分别是O′和A′,则
点O(0,0)和A(1,-2)在l上的射影分别是O′和A′,则![]() e,其中
e,其中![]() = ( )
= ( )
A.![]() B.
B.![]() C.2 D.-2
C.2 D.-2
8.[2004年全国高考(四川云南吉林黑龙江)· 理科数学第14题,文科数学第14题]
设![]() 满足约束条件:
满足约束条件:
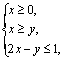
则![]() 的最大值是
.
的最大值是
.
9.[2004年全国高考(四川云南吉林黑龙江)· 理科数学第15题,文科数学第15题]
设中心在原点的椭圆与双曲线![]() =1有公共的焦点,且它们的离心率互为倒数,
=1有公共的焦点,且它们的离心率互为倒数,
则该椭圆的方程是 .
10.[2004年全国高考(陕西广西海南西藏内蒙古)·理科数学第1题,文科数学第1题]
设集合![]() ,
,![]() ,则集合
,则集合![]() 中元素的个数为
( )
中元素的个数为
( )
A.1 B.2 C.3 D.4
11.[2004年全国高考(陕西广西海南西藏内蒙古)·理科数学第4题,文科数学第5题]
圆![]() 在点
在点![]() 处的切线方程为 ( )
处的切线方程为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12.[2004年全国高考(陕西广西海南西藏内蒙古)·理科数学第7题,文科数学第8题]
设双曲线的焦点在![]() 轴上,两条渐近线为
轴上,两条渐近线为![]() ,则该双曲线的离心率
,则该双曲线的离心率![]() ( )
( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
13.[2004年全国高考(陕西广西海南西藏内蒙古)·文科数学第16题]
设P为圆![]() 上的动点,则点P到直线
上的动点,则点P到直线![]() 的距离的最小值为
.
的距离的最小值为
.
14.[2004年全国高考(陕西广西海南西藏内蒙古)·理科数学第16题]
设![]() 是曲线
是曲线![]() 上的一个动点,则点
上的一个动点,则点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到
到![]() 轴的距离之和的最小值为
.
轴的距离之和的最小值为
.
15.[2004年全国高考(甘肃贵州宁夏青海新疆)·理科数学第3题]
过点(-1,3)且垂直于直线![]() 的直线方程为( )
的直线方程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
16.[2004年全国高考(甘肃贵州宁夏青海新疆)·文科数学第7题]
已知函数![]() 的图象有公共点A,且点A的横坐标为2,则
的图象有公共点A,且点A的横坐标为2,则![]() = ( )
= ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
17.[2004年全国高考(甘肃贵州宁夏青海新疆)·文科数学第8题]
已知圆C的半径为2,圆心在![]() 轴的正半轴上,直线
轴的正半轴上,直线![]() 与圆C相切,则圆C的方程为 ( )
与圆C相切,则圆C的方程为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
18.[2004年全国高考(甘肃贵州宁夏青海新疆)·理科数学第8题]
已知椭圆的中心在原点,离心率![]() ,且它的一个焦点与抛物线
,且它的一个焦点与抛物线![]() 的焦点重合,
的焦点重合,
则此椭圆方程为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
19.[2004年全国高考(甘肃贵州宁夏青海新疆)·理科数学第16题,文科数学第16题]
设![]() 满足约束条件:
满足约束条件:
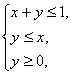 则
则![]() 的最大值是
.
的最大值是
.
20.[(山东山西河南河北江西安徽)·理科数学第21题(12分),文科数学第22题(14分)]
设双曲线C:![]() 相交于两个不同的点A、B.
相交于两个不同的点A、B.
(I)求双曲线C的离心率e的取值范围:
(II)设直线l与y轴的交点为P,且![]() 求a的值.
求a的值.
21.[ (四川云南吉林黑龙江)· 理科数学第21题(12分),文科数学第22题(14分)]
给定抛物线C:y2=4x,F是C的焦点,过点F的直线l与C相交于A、B两点。
(Ⅰ)设l的斜率为1,求![]() 与
与![]() 的夹角的大小;
的夹角的大小;
(Ⅱ)设![]() ,若λ∈[4,9],求l在y轴上截距的变化范围.
,若λ∈[4,9],求l在y轴上截距的变化范围.
22.[(陕西广西海南西藏内蒙古)·理科数学第21题(12分),文科数学第22题(14分)]
设椭圆![]() 的两个焦点是
的两个焦点是![]() 与
与![]() ,且椭圆上存在一点
,且椭圆上存在一点![]() ,使得直线
,使得直线![]() 与
与![]() 垂直.
垂直.
(1)求实数![]() 的取值范围;
的取值范围;
(2)设![]() 是相应于焦点
是相应于焦点![]() 的准线,直线
的准线,直线![]() 与
与![]() 相交于点
相交于点![]() ,若
,若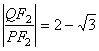 ,求直线
,求直线![]() 的方程.
的方程.
23.[(甘肃贵州宁夏青海新疆)·理科数学第21题(12分),文科数学第22题(14分)]
双曲线![]() 的焦距为2c,直线
的焦距为2c,直线![]() 过点(a,0)和(0,b),且点(1,0)到直线
过点(a,0)和(0,b),且点(1,0)到直线![]() 的距离与点(-1,0)到直线
的距离与点(-1,0)到直线![]() 的距离之和
的距离之和![]() 求双曲线的离心率e的取值范围.
求双曲线的离心率e的取值范围.
参考答案
1.C 2.C 3. x2 +
y2 = 4
4.C 5.B 6.B 7.D
8.5 9.![]()
10.B 11.D 12.C 13.1 14.![]() 15.A 16.A 17.D 18.A 19.2
15.A 16.A 17.D 18.A 19.2
20.[2004年全国高考(山东山西河南河北江西安徽)·理科数学第21题(12分),文科数学第22题(14分)]
本小题主要考查直线和双曲线的概念和性质,平面向量的运算等解析几何的基本思想和综合解题能力.
解:(I)由C与t相交于两个不同的点,故知方程组
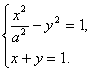
有两个不同的实数解.消去y并整理得
(1-a2)x2+2a2x-2a2=0. ①
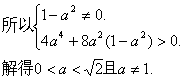
双曲线的离心率

(II)设![]()

由于x1+x2都是方程①的根,且1-a2≠0,

21.[ (四川云南吉林黑龙江)· 理科数学第21题(12分),文科数学第22题(14分)]
本小题主要考查抛物线的性质,直线与抛物线的关系以及解析几何的基本方法、思想和综合解题能力。
解:(Ⅰ)C的焦点为F(1,0),直线l的斜率为1,所以l的方程为![]()
将![]() 代入方程
代入方程![]() ,并整理得
,并整理得 ![]()
设![]() 则有
则有 ![]()
![]()
![]()
![]()
所以![]() 夹角的大小为
夹角的大小为![]()
(Ⅱ)由题设![]() 得
得 ![]()
|

由②得![]() , ∵
, ∵ ![]() ∴
∴![]() ③
③
联立①、③解得![]() ,依题意有
,依题意有![]()
∴![]() 又F(1,0),得直线l方程为
又F(1,0),得直线l方程为
![]()
当![]() 时,l在方程y轴上的截距为
时,l在方程y轴上的截距为![]()
由 ![]() 可知
可知![]() 在[4,9]上是递减的,
在[4,9]上是递减的,
∴
![]()
直线l在y轴上截距的变化范围为![]()
22.[(陕西广西海南西藏内蒙古)·理科数学第21题(12分),文科数学第22题(14分)]
本小题主要考查直线和椭圆的基本知识,以及综合分析和解题能力.
解:(Ⅰ)由题设有![]() 设点P的坐标为
设点P的坐标为![]() 由PF1⊥PF2,得
由PF1⊥PF2,得
![]() 化简得
化简得 ![]() ①
①
将①与![]() 联立,解得
联立,解得 ![]()
由![]() 所以m的取值范围是
所以m的取值范围是![]() .
.
(Ⅱ)准线L的方程为![]() 设点Q的坐标为
设点Q的坐标为![]() ,则
,则
![]()
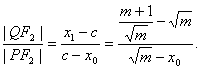 ②
②
将
![]() 代入②,化简得
代入②,化简得 ![]()
由题设 ![]() ,得
,得 ![]() , 无解.
, 无解.
将
![]() 代入②,化简得
代入②,化简得 ![]()
由题设
![]() ,得
,得 ![]() .
.
解得m=2. 从而![]() ,
,
得到PF2的方程 ![]()
23.[(甘肃贵州宁夏青海新疆)·理科数学第21题(12分),文科数学第22题(14分)]
本小题主要考查点到直线距离公式,双曲线的基本性质以及综合运算能力.
解:直线![]() 的方程为
的方程为![]() ,即
,即 ![]()
由点到直线的距离公式,且![]() ,得到点(1,0)到直线
,得到点(1,0)到直线![]() 的距离
的距离
![]() ,
,
同理得到点(-1,0)到直线![]() 的距离
的距离![]()
![]()
由![]() 即
即 ![]()
于是得 ![]()
解不等式,得 ![]() 由于
由于![]() 所以
所以![]() 的取值范围是
的取值范围是
![]()