2005-2006学年度南通市九校(学科基地)联考数学试卷
(南通中学 南通一中 启东中学 海门中学 通州中学 如东中学 栟茶中学 如皋中学 海安中学)
本试卷分第I卷和第II卷两部分,共10页。满分150分,考试时间120分钟。
第Ⅰ卷(选择题共60分)
参考公式:
三角函数的和差化积公式
![]()
![]()
![]()
![]()
若事件A在一次试验中发生的概率是p,则它在n次独立重复试验中恰好发生k次的概率Pn(k)=![]() (
(![]() =0,1,2,…,
=0,1,2,…,![]() )
)
一组数据![]() 的方差
的方差![]()
其中![]() 为这组数据的平均值
为这组数据的平均值
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题意要求的.
1.设集合![]() A∪(CIB)= ( )
A∪(CIB)= ( )
A.{1} B.{1,2} C.{2} D.{0,1,2}
2.抛物线y=ax2的准线方程是y=1,则a的值为 ( )
A.![]() B.
B.![]() C.4
D.-4
C.4
D.-4
3.函数![]() ,(x∈R)的反函数为
( )
,(x∈R)的反函数为
( )
A.![]() , x∈R B.
, x∈R B.![]() ,x∈(0,+∞)
,x∈(0,+∞)
C.![]() , x∈R D.
, x∈R D.![]() ,x∈(0,+∞)
,x∈(0,+∞)
4.在坐标平面上,不等式组![]() 所表示的平面区域的面积为
( )
所表示的平面区域的面积为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知直线m、n与平面α、β,给出下列三个命题: ( )
①若![]() ②若
②若![]()
③若![]() 其中真命题的个数是
其中真命题的个数是
A.0 B.1 C.2 D.3
6.已知数列{an}中,![]() ,(
,(![]() ∈N+),则在数列{an}的前50项中最小项和最大项分别是
( )
∈N+),则在数列{an}的前50项中最小项和最大项分别是
( )
A.a1 ,a50 B.a1, a8 C.a8, a9 D.a9, a50
7.O是平面上一定点,A,B,C是平面上不共线的三个点,动点P满足![]() ,λ∈[0,+∞),则P的轨迹一定通过△ABC的
( )
,λ∈[0,+∞),则P的轨迹一定通过△ABC的
( )
A.外心 B.垂心 C.内心 D.重心
8.已知sinx-siny= -![]() ,cosx-cosy=
,cosx-cosy= ![]() ,且x,y为锐角,则tan(x-y)的值是 ( )
,且x,y为锐角,则tan(x-y)的值是 ( )
A.![]() B.-
B.-![]() C.±
C.±![]() D.
D.![]()
9.已知点P(m,3)是抛物线y=x2+4x+n上距点A(-2,0)最近一点,则m+n= ( )
A.1 B.3 C.5 D.7
10.已知双曲线![]() -
-![]() =1(a>0,b>0)的右焦点为F,右准线与一条渐近线交于点A,△OAF的面积为
=1(a>0,b>0)的右焦点为F,右准线与一条渐近线交于点A,△OAF的面积为![]() (O为原点),则两条渐近线的夹角为
( )
(O为原点),则两条渐近线的夹角为
( )
A.30º B.45º C.60º D.90º
11.方程![]() 所表示的曲线是 ( )
所表示的曲线是 ( )
A.焦点在x轴上的椭圆 B.焦点在x轴上的双曲线
C.焦点在y轴上的椭圆 D.焦点在y轴上的双曲线
12.4位同学参加某种形式的竞赛,竞赛规则规定:每位同学必须从甲、乙两道题中任选一题作答,选甲题答对得21分,答错得-21分;选乙题答对得7分,答错得-7分.若4位同学的总分为0,则这4位同学不同得分情况的种数是 ( )
A.48 B.44 C.36 D.24
 2005-2006学年度南通市九校(学科基地)联考数学试卷
2005-2006学年度南通市九校(学科基地)联考数学试卷
第Ⅱ卷(非选择题共90分)
注意事项:
1.第二卷共6页,用钢笔或圆珠笔直接答在试题纸上。
2.答卷前将密封线内的项目填写清楚。
| 题号 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 结分人 | 复分人 |
| 得分 |
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
四、(21分)
二、填空题:本大题共6小题,每小题4分,共24分. 把答案填在答题卡相应位置.
13.函数![]() 的单调递减区间为
.
的单调递减区间为
.
14.若不等式x-4+3-x<a的解集是空集,则实数a的取值范围是 .
15.已知![]() 的展开式中
的展开式中![]() 的系数与
的系数与![]() 的展开式中x3的系数相等,
的展开式中x3的系数相等,
则![]() =
=
16.一工厂生产了某种产品180件,它们来自甲、乙、丙3条生产线,为检查这批产品的质量,决定采用分层抽样的方法进行抽样,已知甲、乙、丙三条生产线抽取的个体数组成一个等差数列,则乙生产线生产了 件产品.
17.正四棱锥的一个对角面的面积是一个侧面面积的![]() 倍,则侧面与底面所成锐二面角
倍,则侧面与底面所成锐二面角
等于 .
18. 以下四个关于圆锥曲线的命题中
①设A、B为两个定点,k为非零常数,![]() ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;
②过定圆C上一定点A作该圆的动弦AB,O为坐标原点,若![]() 则动点
则动点![]() 的轨迹为椭圆;
的轨迹为椭圆;
③方程![]() 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
④双曲线![]() 有相同的焦点.
有相同的焦点.
其中真命题的序号为 (写出所有真命题的序号)
三、解答题:本大小题共5小题,共66分. 解答应写出文字说明、证明过程或演算步骤.
![]()
19.(本小题满分12分)
已知向量![]() (
(![]() ) 和
) 和![]() =(
=(![]() ),
),![]() ∈[π,2π].
∈[π,2π].
(1) 求![]() 的最大值;(2)当
的最大值;(2)当![]() =
=![]() 时,求
时,求![]() 的值.
的值.
![]()
20、(本小题满分12分)口袋里装有红色和白色共36个不同的球,且红色
球多于白色球.从袋子中取出2个球,若是同色的概率为![]() ,求:
,求:
(1) 袋中红色、白色球各是多少?
(2) 从袋中任取3个小球,至少有一个红色球的概率为多少?
![]()
21.(本小题满分14分)如图正方体在ABCD-A1B1C1D1中,E,F,G分别为AB,B1C1,AA1的中点,
 (1) 求证:EF⊥平面GBD;
(1) 求证:EF⊥平面GBD;
(2) 求异面直线AD1与EF所成的角 .
![]() 22.(本小题满分14分)已知椭圆C的方程为
22.(本小题满分14分)已知椭圆C的方程为![]() ,双曲线
,双曲线![]() 的两条渐近线为
的两条渐近线为![]() ,过椭圆C的右焦点F的直线
,过椭圆C的右焦点F的直线![]() ,又
,又![]() 与
与![]() 交于P点,设
交于P点,设![]() 与椭圆C的两个交点由上至下依次为A,B.
与椭圆C的两个交点由上至下依次为A,B.
(1) 当![]() 与
与![]() 夹角为
夹角为![]() 且
且![]() 时,求椭圆C的方程.
时,求椭圆C的方程.
(2) 求![]() 的最大值.
的最大值.

![]() 23.(本小题满分14分)设
23.(本小题满分14分)设![]() =
=![]() (a>0)为奇函数,且
(a>0)为奇函数,且
![]() min=
min=![]() ,数列{an}与{bn}满足 如下关系:a1=2,
,数列{an}与{bn}满足 如下关系:a1=2, ![]() ,
,![]() .
.
(1)求f(x)的解析表达式;
(2) 证明:当n∈N+时, 有bn![]()
![]() .
.
九校联考数学参考答案
一.选择题:
1.D 2.B 3.A 4.B 5.C 6.C 7.D 8.B 9.C 10.D 11.C 12.B
二.填空题:
13.(0,1) 14.(-∞,1] 15.![]() 16.60 17.
16.60 17.![]() 18.③、④
18.③、④
三.解答题:
19.解:(1) ![]() (2分)
(2分)
![]() =
=
![]() =
=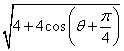 =
=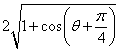 (4分)
(4分)
∵θ∈[π,2π],∴![]() ,∴
,∴![]() ≤1
≤1
![]() max=2
max=2![]() .
(6分)
.
(6分)
(2)
由已知![]() ,得
,得![]() (8分)
(8分)
又![]() ∴
∴![]() (10分)
(10分)
∵θ∈[π,2π]∴![]() ,∴
,∴![]() . (12分)
. (12分)
20.解:(1)令红色球为x个,则依题意得![]() ,
(3分)
,
(3分)
所以![]() 得x=15或x=21,又红色球多于白色球,所以x=21.所以红色球为21个,白色球为15个.
( 6分)
得x=15或x=21,又红色球多于白色球,所以x=21.所以红色球为21个,白色球为15个.
( 6分)
(2)设从袋中任取3个小球,至少有一个红色球的事件为A,均为白色球的事件为B,
则P(B)=1--P(A)=![]() =
=![]() (12分)
(12分)
21.解法一:(1)取BC的中点H,连EH,易得EH是EF在平面AC上的射影,
∵BD⊥EH,∴由三垂线定理,得 EF⊥BD; (4分)
又∵EF在平面AB1上的射影是B1E,由△BB1E∽△ABG,得B1E⊥BG,
∴由三垂线定理,得 EF⊥BG,
∵BG∩BD=B,∵EF⊥平面GBD. (8分)
(2)取C1D1的中点M,连EM,易得EM∥AD1,
所以∠EFM就是异面直线AD1与EF所成的角, (11分)
∵MF∥BD,∴EF⊥MF
在Rt△EFM中,由EM=![]() ,(a为正方体的棱长),EF=
,(a为正方体的棱长),EF=![]() ,得
,得
∠EFM=30º.即异面直线AD1与EF所成的角为30º. (14分)
解法二:(向量法)
(1) 以AD为x轴,DC为y轴,DD1为z轴建立空间坐标系,不妨设正方体的棱长为2,
则D(0,0,0),A(2,0,0),B(2,2,0),E(2,1,0),F(1,2,2),G(2,,0,1)
D1(0,0,2 ) (4分)
∵![]() (2,2,0)·(1,-1,-2)=0,
(2,2,0)·(1,-1,-2)=0,![]() (0,-2,1)·(1,-1,-2)=0
(0,-2,1)·(1,-1,-2)=0
∴![]() ,
,![]() ,又∵BG∩BD=B,∵EF⊥平面GBD.
(8分)
,又∵BG∩BD=B,∵EF⊥平面GBD.
(8分)
(2)![]() =(-2,0,2),
=(-2,0,2),![]() =(1,-1,-2)
=(1,-1,-2)
![]() =
=![]() ,
,
即异面直线AD1与EF所成的角为30º. (14分)
![]()
![]() 22.解:(1)
22.解:(1)![]()
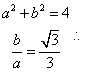
![]() 故
故 (6分)
(6分)
(2)![]() 联立
联立![]() 得
得![]() (8分)
(8分)
设A分![]() 的比为
的比为![]() ,则A
,则A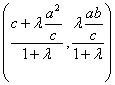
代入![]() ,整理化简得:
,整理化简得:![]() (12分)
(12分)
![]() 即
即![]() 的最大值为
的最大值为![]() (14分)
(14分)
23.解:由f(x)是奇函数,得 b=c=0, (3分)
由f(x)min=![]() ,得a=2,故f(x)=
,得a=2,故f(x)= ![]() (6分)
(6分)
(2) ![]() =
= ,
,
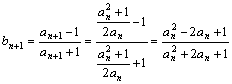 =
=![]() =
=![]() (8分)
(8分)
∴![]() =
=![]() =
=![]() =…=
=…=![]() ,而b1=
,而b1=![]()
∴![]() =
=![]() (10分)
(10分)
当n=1时, b1=![]() ,命题成立,
(12分)
,命题成立,
(12分)
当n≥2时
∵2n-1=(1+1)n-1=1+![]() ≥1+
≥1+![]() =n
=n
∴![]() <
<![]() ,即 bn≤
,即 bn≤![]() .
(14分)
.
(14分)
注:不讨论n=1的情况扣2分.