已知双曲线C的实半轴长和虚半轴长的乘积为
，C的两个焦点分别为F1、F2，直线L过F2且与直线F1F2的夹角为
，tg=
，L与线段F1F2的垂直平分线的交点是P，线段PF2与双曲线C的交点为Q(且｜PQ｜∶｜PF2=2∶1)，求双曲线的方程.
解：如图，
以直线F1F2为x轴，线段F1F2的垂直平分线为y轴建立坐标系.
设双曲线C的方程为
-
=1 (a＞b＞0)
设F1，F2的坐标分别为(-c,0)、(c,0)，其中C=
，则点P的坐标为(0，-，c).
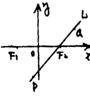由线段的定比分点公式可得Q点的坐标为(
c,- c).
将Q点坐标代入双曲线方程得
-
=1，整理得
16(
)4-41()2-21=0
解得()2=3或()2=-
(舍去)
由()2=3和题设ab=，解得a=1，b=.
故所求双曲线方程为x2-
=1.
已知点P在直线x=2上移动，直线l通过原点且OP垂直 ，过点A(1，0)和点P的直线m和直线l交于点Q，求点Q的轨迹方程，并指出该轨迹的名称和它 的焦点坐标.
解：设点P的坐标为(2，y1)，则直线OP的斜率
kOP=
.
∵l⊥直线OP.
∴直线l的斜率k1满足kOP·k1=-1，即·k1=-1，得k 1=-
.
又直线l过原点，所以l的方程为y=-x.
∵直线m过点A(1，0)，P(2，y1).
∴m的方程为y1x-y-y1=0
由l的方程得y1=-
代入m的方程得--x-y+=0，即2x2+y2-2x=0.
显然点Q与点A(1，0)不重合，故x≠1.
又2x2+y2-2x=0可化为
+
=1 (x≠1)，
已知椭圆的焦点为F1(0，-1)和F2(0，1)，直线 y=4是椭圆的一条准线.
(1)求椭圆方程；
(2)设点P在椭圆上，且│PF1│-│PF2│=1，求
tan∠F1PF2的值.
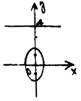解：如图.
(1)设所求椭圆方程为
+
=1，(a＞ b＞0)
由F1(0，-1)和F2(0，1)，知c=1，得a2=b2+1， ①
由一条准线方程为y=4知，
=4 ②
又a2=b2+c2 ③
由①、②、③解得a2=4，b2=3.
故所求椭圆方程为
+
=1.
(2)由椭圆定义及a=2有│PF1│+│PF2│=4 ①
由题设有│PF1│-│PF2│=1 ②
解出│PF1│=
，│PF2│=
，又│F1F2 │=2.
在△PF1F2中，∠F1PF2=θ，
∴cosθ=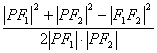
=
，
从而sinθ=
，tgθ=
，tg∠F1PF2=.
四、能力训练
(一)选择题
1.“点M的坐标是方程f(x，y)=0的解”是“点M在方程f(x，y)=0曲线上”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既非充分又非必要条件
2.抛物线x=-
的焦点坐标是( )
A.(0，1) B.(-1，0)
C.(0，-
)
D.(-，0)
3.椭圆(1-m)x2-my2=1的长轴长是( )
A.
B. 
C. 
D.
4.下列各对双曲线中，既有相同离心率又有相同渐近线的是( )
A.-y2=1和
-=1
B. -y2=1和y2-=1
C.y2-=1和x2-
=1
D. -y2=-1和-
=1
5.抛物线x2-4y=0上一点P到焦点的距离为3，那么P的纵坐标是( )
A.3
B.2
C.
D.-2
6.已知椭圆
+
=1 (a＞b＞0)的两 个焦点把夹在两条准线间的线段三等分，那么这个椭圆的离心率是( )
A.
B. 
C.
D. 
7.圆x2+y2-2axsinα-2bycosα-a2cos2α=0在x轴上截得的弦长是( )
A.2a B.2│a│ C.
│a│ D.4│a│
8.过双曲线的一个焦点，有垂直于实轴的弦PQ，F′是另一个焦点，若∠PF′Q=
，则双曲线离心率是( )
A.+2 B. +1 C. D. -1
9.抛物线y2+4y-4x=0的准线方程是( )
A.x=0 B.y=0 C.x=-2 D.y=-2
10.椭圆的两准线方程分别为x=
，x=-
，一个 焦点坐标为(6，2)，则椭圆方程是( )
A.
+
=1
B.
+
=1
C.
+=1
D.
+=1
11.设双曲线-=1的两条渐近线含 实轴的夹角为θ，而离心率e∈［，2］，则θ的取值范围是( )
A.［
，］
B.［
，］
C.［，
］
D.［，π］
12.椭圆+=1的弦AB被点(1，1)平分，则 AB所在的直线方程是( )
A.4x-9y-11=0 B.4x+9y-13=0
C.9x+4y-10=0 D.9x-4y-5=0
13.和x轴相切，且和圆x2+y2=1外切的动圆圆心的轨迹方程是( )
A.x2=2y+1 B.x2=-2y+1
C.x2=2y+1或x2=-2y+1 D.x2=2│y│+1
14.如果椭圆
+
=1 (a＞b＞0)和曲线
+
=1(m＞0，n＞0)有相同的焦点F1和F2 ，P是这两条曲线的交点，则│PF1│·│PF2│的值是( )
A.a-m
B.
(a-m)
C.a2-m2
D.
-
15.已知0＜a＜1＜b，那么曲线a2x2-a2y2=logab是( )
A.焦点在x轴的双曲线
B.焦点在y轴的椭圆
C.焦点在x轴的等轴双曲线
D.焦点在y轴的等轴双曲线
(二)填空题
16.直线xsinα+ycosα=m(常量α∈(0，)) 被圆x2+y2=2所截的弦长为，则m=________.
17.设椭圆
-
=1的准 线平行于x轴，则m的取值范围是________.
18.如果方程x2cos2θ+y2sinθ=1，表示椭圆，那么θ 角的取值范围是_________.
19.设双曲线C：
-
=1椭圆的焦点恰为双 曲线C实轴上的两个端点，椭圆与双曲线离心率为互为倒数，则此椭圆方程是________.
(三)解答题
20.已知两圆C1∶x2+y2+4x-4y-5=0
C2∶x2+y2-8x+4y+7=0
(1)证明此两圆相切，并求过切点的公切线方程.
(2)求过点(2，3)且与两圆相切于上述切点的圆的方程.
21.(1)椭圆+=1上一点P与两焦点 F1F2连线所成的角∠F1PF2=α，求△F1PF2的面积；
(2)将上题的椭圆变成双曲线-=1 ，求△F1PF2的面积.
22.抛物线的顶点在原点，它的准线过双曲线-=1的一个焦点，并与双曲线的实轴垂直，又双曲线与抛物线的一个交点是(1.
5，
)，求抛物线和双曲线的方程.
23.已知椭圆
+
=1，左、右焦点分别为 F2、F1，右准线为L，问能否在椭圆上求得一点P，使│PF1│是P到L的距离d与│PF2│的比例中项?若能，求出P点坐标，若不能，说明理由.
24.试就k的取值(k∈R，且k≠4)讨论方程
+(k-2)y2=1+k所表 示曲线的形状.
25.已知椭圆
+
=1中有一内接△PAB，∠X
OP=60°，且kPA+kPB=0
(1)求证：直线AB斜率是定值；
(2)求△ABP的面积的最大值.
能力训练参考答案
(一)1.C 2.B 3.C 4.D 5.B 6.D 7.B 8.B 9.C 10.C 11.C 12.B 13.D 14.A 15.D
(二)16.±
；17.(-，-)；18.2kπ＜θ＜2kπ+
或2kπ+＜θ＜2kπ+π(k∈ Z)；19. +=1
(三)20.解 两圆方程化为：c1：(x+2)２+(y-2)２=13 C2∶(x-4)２+(y+2)２=13 ，C1、c２圆心分别为(-2，2)、(4，-2)，半径都是
，圆心距d=
=2，即圆心距等于两圆半径之和，故两 圆外切，因连心线斜率为k1=
=-，解方 程组
x２＋y２+4x-4y-5=0
x２＋y２-8x+4y+7=0
得切点坐标为(1 ，0)，∴公切线方程为y=(x-1),即3x-2y-3=0,(两圆相外切时，两圆方程相
减得根轴方程，即过切的公切线方程).(2)与两圆相切于点(1，0)的圆圆心必在直线y=-(x-1)上，且(x-1)２+y２=(x-2)２+(y-3)２，解上面两方程组成的方程组得圆心坐标为(-4，
)，r２=
,∴所求圆方程为(x-4)２+(y-)２= ,即3x２+3y２+24x-20y-2 7=0.
21.(1)(2c)２=PF1２+PF2２-2PF1PF2cosa=(PF1+PF2)２-2PF1PF2(1+cosa) ∴PF1·PF2=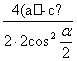
,S=PF1PF2sina=b２tg
,
(2)(2c)２=(PF1-PF2)２+2PF1PF2(1-cosα)，P F1·PF2=
,S=b２ctg.
22.双曲线焦距是2
设抛物线方程为y２=4
;(1.5,)在其上，∴=1故抛物线方程为y２=4x,又
-
=1,a２+b２=1,∴双曲线方程是4x２-
=1;
23.a=5,b=
,c=2,e=,设若有点P，使PF1２=d·PF2， 即
=
=
= PF1+PF2=10，PF1+PF2=10；PF2=
；PF1= PF2=
;PF1-PF2=
＞2c，∴P不存在；
24.k＜-1或k＞4实轴在y轴上的双曲线；-1＜k＜2，实轴在x轴上的双曲线2＜k＜4,k=3时， 圆k≠3，即k∈(2,3)∪(3,4)是长轴为y轴的椭圆.
y=x
25.(1)
P(1， )，
+
=1
由kPA+kPB=0
LPA∶y-=k(x-1) LPB：y- =-k(x-1)可求得
xA=
xB=k２+2 k-3
kAB＝(定值)，
yB=
yB＝
(2)｜AB｜ ＝
，P到AB的距离d=
，S△PAB＝｜AB｜·d＝
≤，S△PAB最大值是.