函数与不等式客观题强化训练
命题人:陈文运
姓名: 学号:
1.设集合M=![]() ,N=
,N=![]() ,映射
,映射![]() ,使对任意的
,使对任意的![]() ,都有
,都有![]() 是奇数,这样的映射
是奇数,这样的映射![]() 的个数是 ( )
的个数是 ( )
(A) 22 (B) 15
(C) 50 (D) 27
2.设A={![]() │
│![]() },B={
},B={![]() │
│![]() },在图(1)中,能表示从A到B的映射是( )
},在图(1)中,能表示从A到B的映射是( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 2 2 2 2
2 2 2 2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 1 1 1 1
1 1 1 1
![]()
![]()
![]() 0 1 2
0 1 2
0 1 2
0 1 2
0 1 2
0 1 2
0 1 2
0 1 2
(A) (B) (C) (D)
图(1)
![]()
![]()
![]()
![]()
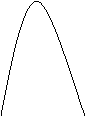
![]() 3.给出某运动的速度曲线如图所示,从以下运动中选出一种,其变化速度最符合图中的曲线是( )
3.给出某运动的速度曲线如图所示,从以下运动中选出一种,其变化速度最符合图中的曲线是( )
(A) 钓鱼 (B) 跳高
(C) 100米赛跑 (D) 掷标枪
图(2)
4.奇函数![]() 有反函数
有反函数![]() ,则必在
,则必在![]() 的图象上的点是( )
的图象上的点是( )
(A)
![]() (B)
(B)
![]()
(C)
![]() (D)
(D)
![]()

![]() 5.定义在R上的函数
5.定义在R上的函数![]() 是单调递减函数,如图所示,给出四个结论:1
是单调递减函数,如图所示,给出四个结论:1![]() ;2
;2![]() ;3
;3![]() ;4
;4![]() y
y
其中正确结论的个数是( )
![]()
![]() (A) 1
(B) 2
1
(A) 1
(B) 2
1
![]() (C) 3
(D) 4 0 1
x
(C) 3
(D) 4 0 1
x
图(3)
6.设偶函数![]() 在
在![]() 上递增,则
上递增,则![]() 的大小关系是( )
的大小关系是( )
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
不能确定
(D)
不能确定
7.设![]() ,
,![]()
![]() ,
,![]() 的大小关系是( )
的大小关系是( )
(A)![]() (B)
(B)
![]()
(C) ![]() (D)
(D)
![]()
8.已知定义域为R的偶函数![]() 上是增函数,且
上是增函数,且![]() ,则不等式
,则不等式![]() 的解集是( )
的解集是( )
(A) {![]() │
│![]() }
(B) {
}
(B) {![]() │
│![]() }
}
(C) {![]() │
│![]() 或
或![]() }
(D) {
}
(D) {![]() │
│![]() 或
或![]() }
}
9.设函数 ,已知
,已知![]() ,则实数
,则实数![]() 的取值范围是( )
的取值范围是( )
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D)
![]()
10.设![]() 是两个实数,给出下列条件:1
是两个实数,给出下列条件:1![]() ;2
;2![]() ;3
;3![]() ;4
;4![]() ;5
;5![]() 。其中能推出“
。其中能推出“![]() 中至少有一个数大于1”的条件是( )
中至少有一个数大于1”的条件是( )
(A) 23 (B) 123
(C) 345 (D) 3
11.在区间![]() 上,函数
上,函数![]() 与
与![]() 在同一点取得相同的最小值,那么
在同一点取得相同的最小值,那么![]() 在区间
在区间![]() 上的最大值为( )
上的最大值为( )
(A) ![]() (B) 4
(C) 8
(D)
(B) 4
(C) 8
(D) ![]()
12.若二次函数![]() 在区间
在区间![]() 内至少存在一点C(
内至少存在一点C(![]() 使
使![]() ,则实数
,则实数![]() 的取值范围是( )
的取值范围是( )
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D)
![]() 或
或![]()
13.已知![]() ,“
,“![]() ”是“
”是“![]() ”的( )
”的( )
(A) 充分非必要条件 (B) 必要非充分条件
(C) 充要条件 (D) 非充分非必要条件
14.若方程![]() 只有一解,则实数
只有一解,则实数![]() 的取值范围是( )
的取值范围是( )
(A) ![]() (B)
(B)
![]()
(C) ![]() ∪
∪![]() (D)
(D) ![]()
15.拟定从甲地到乙地通话![]() 分钟的电话费由
分钟的电话费由![]() 给出,其中
给出,其中![]() ,
,![]() 是大于或等于
是大于或等于![]() 的最小整数。则从甲地到乙地通话时间为5.5分钟的话费为( )
的最小整数。则从甲地到乙地通话时间为5.5分钟的话费为( )
(A) 3.71 (B) 3.97 (C) 4.24 (D) 4.78
16.对任意![]() ,函数
,函数![]() 的值总大于0,则
的值总大于0,则![]() 的取值范围是( )
的取值范围是( )
(A) {![]() │
│![]() }
(B) {
}
(B) {![]() │
│![]() }
}
(C) {![]() │
│![]() } (D)
{
} (D)
{![]() │
│![]() }
}
![]()
![]()
![]()
![]() 17.某汽车运输公司,购买了一批豪华大客车投入营运,据市场分析每辆客车营运的总利润
17.某汽车运输公司,购买了一批豪华大客车投入营运,据市场分析每辆客车营运的总利润![]() (单位:10万元)与营运年数
(单位:10万元)与营运年数![]() 成二次函数11
成二次函数11
如图(4)所示,则每辆客车营运多少年,其营运的年平均
![]()
![]()
![]() 利润最大?( )
7
利润最大?( )
7
(A) 3 (B) 4
![]() (C) 5
(D) 6
(C) 5
(D) 6
![]() 0
4 6 9 x
0
4 6 9 x
图(5)
18.某人骑自行车沿直线匀速旅行,先前进了![]() 千米,休息了一段时间,又沿原路返回
千米,休息了一段时间,又沿原路返回![]() 千米(
千米(![]() ,再前进
,再前进![]() 千米,则此人离起点的距离
千米,则此人离起点的距离![]() 与时间
与时间![]() 的关系示意图是( )
的关系示意图是( )
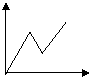 |  | 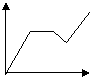 | 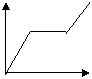 |
(A) (B) (C) (D)
19.已知圆台的侧面积为![]() ,母线和底面所成的角为60
,母线和底面所成的角为60![]() ,若记中截面圆的半径为
,若记中截面圆的半径为![]() ,较大的底面圆的半径为
,较大的底面圆的半径为![]() ,则函数
,则函数![]() 的图像是( )
的图像是( )
![]()

![]()
![]()
![]()
![]()
![]() y
y y y
y
y y y



 2 2
2 2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 1
1 ![]()
![]()
![]()
![]()
![]()
![]() 0 1 x 0 1 x
0 1 x 0 1 x
0 1 x 0 1 x
0 1 x 0 1 x
(A) (B) (C) (D)
![]() 20.已知函数
20.已知函数![]()
![]() 满足:对任意实数
满足:对任意实数![]() ,都有
,都有![]() 并且
并且![]()
![]()
![]() ,试写出一个满足这些条件的函数
,试写出一个满足这些条件的函数![]() =
=
21.老师给出一个函数![]()
![]() ,四个学生甲、乙、丙、丁各指出这个函数的一个性质:甲:对于
,四个学生甲、乙、丙、丁各指出这个函数的一个性质:甲:对于![]() ,都有
,都有![]() ;乙:在
;乙:在![]() 上函数递减;丙:在
上函数递减;丙:在![]() 上函数递增;丁:
上函数递增;丁:![]() 不是函数的最小值。如果其中恰有三人说得正确,请写出一个这样的函数
不是函数的最小值。如果其中恰有三人说得正确,请写出一个这样的函数
![]() 22.设函数
22.设函数![]() 的定义域为R,则下列命题中:1
的定义域为R,则下列命题中:1![]()
![]() 是偶函数,则
是偶函数,则![]()
![]() 的图像关于
的图像关于![]() 轴对称;2若
轴对称;2若![]()
![]() 是偶函数,则
是偶函数,则![]()
![]() 的图像关于直线
的图像关于直线![]() 对称;3若
对称;3若![]() ,则
,则![]()
![]() 的图像关于直线
的图像关于直线![]() 对称;4
对称;4 ![]()
![]() 和
和![]()
![]() 的图像关于直线
的图像关于直线![]() 对称。其中正确命题的序号为
对称。其中正确命题的序号为
![]() 23.设函数
23.设函数![]() =
=![]() ,
,![]() ,关于
,关于![]() 有下列命题:1
有下列命题:1![]() 是偶函数;2
是偶函数;2![]() 在区间
在区间![]() 上是增函数;3
上是增函数;3![]() 在区间
在区间![]() 上是增函数;4
上是增函数;4![]() 有最小值-1。其中正确命题的序号为
有最小值-1。其中正确命题的序号为
![]()
24.已知三个不等式:1![]() ;2
;2![]() ;3
;3![]() ;以其中两个作为条件,余下一个作结论,则可以组成
个正确的命题。
;以其中两个作为条件,余下一个作结论,则可以组成
个正确的命题。
![]()
![]() 25.已知
25.已知![]() 是实数,给出下列四个论断:1
是实数,给出下列四个论断:1![]() ;2
;2![]()
![]() ;3
;3![]() ;4
;4![]() 。以其中两个论断作为条件,其余两个论断作为结论,写出你认为正确的一个命题:
。以其中两个论断作为条件,其余两个论断作为结论,写出你认为正确的一个命题:
函数与不等式客观题强化训练参考答案
CDCBD BDCBD BBACC BCCB
20. ![]()
21.![]()
22.②、④
23.①、③、④
24.3
25.①③![]() ②④
②④
另:
12.分类讨论法:(1)![]() ;(2)
;(2)![]() ;
;
(3)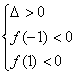
17.由 ![]() 知:当且仅当x=5取最大值。
知:当且仅当x=5取最大值。