06届黄冈中学高考数学第三轮综合能力测试题(二)
一、选择题
1．若f(x)和g(x)都是定义在R上的函数，且均存在反函数，则函数f[g(x)]的反函数为( )
A．f－1[g－1(x)] B．f－1[g(x)] C．g－1[f－1(x)] D．g－1[f(x)]
2．若奇函数f(x)＝kax－ax(a＞0且a≠1)在R上是增函数，则g(x)＝loga()的大致图象是( )
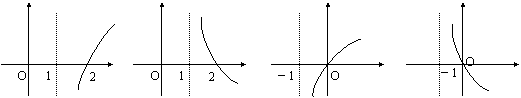
A B C D
3．要得到函数y＝cos(2x－)＋1的图象，只需将函数y＝sin2x的图象作下列平移，其中正确的平移是( )
A．按＝(－，1)平移 B．按＝(，－1)平移
C．按＝(－，1)平移 D．按＝(，－1)平移
4．实系数方程x2＋ax＋2b＝0的一个根大于0且小于1，另一个根大于1且小于2，则的取值范围是( )
A．(，1) B．(，1) C．(－，) D．(－，)
5．f(x)是偶函数，且f(x)在[0，＋∞]上是增函数，如果f(ax＋1)≤f(x－2)在x∈[，1]上恒成立，则实数a的取值范围是( )
A．[－2，0] B．[－5，0] C．[－5，1] D．[－2，1]
6．设a、b、c∈R＋，且＋＝1，则使a＋b≥c恒成立的c的取值范围是( )
A．(0，8] B．(0，10] C．(0，14] D．(0，16]
7．过点A(1，4)，且纵横截距的绝对值相等的直线条数为( )
A．1 B．2 C．3 D．4
8．若命题P：x∈A∩B，则¬P( )
A．x∈A且x∈B B．x∈A或x∈B C．x∈A且x∈B D．x∈A∪B
9．下列命题中，正确的个数是( )
①若＋＝0，则＝＝；②在△ABC中，若＋＋＝
，则O为△ABC的重心；③若，是共线向量，则·＝·，反之也成立；④若，是非零向量，则＋＝的充要条件是存在非零向量，使·＋·＝0．
A．1 B．2 C．3 D．4
10．在正三棱锥P－ABC中，M、N分别是PB、PC的中点，若截面AMN⊥侧面PBC，则此棱锥侧面与底面所成的二面角是( )
A． B． C．arccos D．arccos
11．某地举行一次民歌大奖赛时，六个省各有一对歌手参加决赛，现要选出4名优胜者，则选出的4名选手中有且只有两个人是同一省份的歌手的概率为( )
A． B． C． D．
12．已知数列{an}对于任意的n∈N＊，满足＝an·an＋4，且a3＝2，a7＝4，则a15的值是( )
A．8 B．12 C．16 D．32
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题
13．直线L的方程为：x＋2ycosθ＝－3(θ∈R)，则直线L的倾斜角α的取值范围是＿＿＿＿＿．
14．若a1(x－1)4＋a2(x－1)3＋a3(x－1)2＋a4(x－1)＋a5＝x4，则a2－a3＋a4＝＿＿＿＿．
15．一个正方体，它的表面涂满了红色，在它的相邻三个面上各切两刀，可得27个小立方块，从中任取2个，其中恰有1个一面涂有红色，另一个两面涂有红色的概率为＿＿＿＿．
16．下面是关于三棱锥的四个命题：
①底面是等边三角形，侧面与底面所成的二面角都相等的三棱锥是正三棱锥；
②底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥；
③底面是等边三角形，侧面的面积都相等的三棱锥是正三棱锥；
④侧棱与底面所成的角都相等，且侧面与底面所成的二面角都相等的三棱锥是正三棱锥．
其中真命题的编号是＿＿＿＿＿＿．
三、解答题
17．设函数f(x)＝·，其中＝(2cosx，1)，＝(cosx，sin2x)，x∈R．
(1)若f(x)＝1－，且x∈[－，]，求x；
(2)若函数y＝2sin2x的图象按向量＝(m，n)(m＜)平移后得到函数y＝f(x)的图象，求实数m、n的值．
18．若方程k－4－y－1＋3·2－y－1＝0有实根，求实数k的取值范围．
19．如图，AB为⊙O的直径，MB⊥⊙O所在平面于点B，C为⊙O上一点，MB＝4，AC＝BC＝2．
(1)证明：平面MAC⊥平面MBC；
(2)求MA与BC所成角的大小．
20．如图，公园有一块边长为2a的等边△ABC的边角地，现修成草坪，图中DE把草坪分成面积相等的两部分，D在AB上，E在AC上．
(1)设AD＝x(x≥0)，ED＝y，求用x表示y的函数关系式；
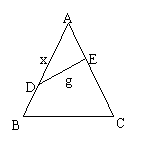(2)如果DE是灌溉水管，为节约成本，希望它最短，DE的位置应在哪里？如果DE是参观线路，则希望它最长，DE的位置又应在哪里？请予证明．
21．在以O为原点的直角坐标系中，点A(4，－3)为△AOB的直角顶点，已知AB＝2OA，且B点纵坐标大于零．
(1)求向量AB的坐标；(2)求圆x2＋y2－6x＋2y＝0关于直线OB对称的圆的方程；
(3)是否存在实数a，使抛物线y＝ax2－1上总有关于直线OB对称的两个点，若不存在，说明理由，若存在，求出a的取值范围．
22．已知集合M是同时满足下列两个性质的函数f(x)的全体：①f(x)在其定义域上是单调增函数或单调减函数；②在f(x)的定义域内存在区间[a，b]，使得f(x)在[a，b]上的值域是[a，b]．
(1)判断函数y＝－x3是否属于集合M？并说明理由．若是，请找出区间[a，b]．
(2)若函数y＝＋t∈M，求实数t的取值范围．
2006届高三数学第三轮复习训练题(二)参考答案
1．C 2．D 3．A
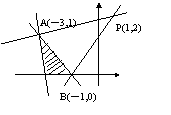
4．A 解：
作平面区域，kPA≤≤kPB．
5．A 解：ax＋1≤x－2，∵≤x≤1，∴x－2≤ax＋1≤2－x1－≤a≤－1，又1≤≤2，∴1－≤－2，－1≥0．故得－2≤a≤0．
6．D 7．C 8．B 9．B 10．D 11．A
12．C 解：a＝a3·a7＝8，∴a5＝±2，＝＝±．
∴数列{a2k＋1}是以±为公比的等比数列，a15＝a7·(±)4＝16．
13．[arctan，π－arctan]．
14．2 解：a1＝1，令x＝1，a5＝1，令x＝0，a1－a2＋a3－a4＋a5＝0．
15． 解：一面红6个，二面红12个，三面红8个，无红1个，P(A)＝＝．
16．①、④．
17．解：(1)f(x)＝·＝1＋2sin(2x＋)＝1－sin(2x＋)＝－，－≤x≤，∴－≤2x＋≤，∴2x＋＝－，∴x＝－．
(2)由(1)得f(x)＝2sin2(x＋)＋1，m＜．∴m＝－，n＝1．
18．解：令t＝2－y－1，0＜t≤1，方程化为t2－3t－k＝0
设f(t)＝t2－3t－k(0＜t≤1＝，对称轴t＝＞1．
∴f(t)在(0，1)上单减，要使f(t)＝0在(0，1)上有解．
∴－2≤k＜0．
19．解：(1)∵AB为⊙O直径，∴BC⊥AC，又MB⊥⊙O所在平面，
∴AC⊥面MBC，又AC
面MAC，∴面MAC⊥面MBC．
(2)连CO延长交圆于D，∴ACBD为正方形，∴AD BC，
记∠MAD＝α即为所求．又MD＝＝．
AM＝＝＝．AD＝2．
∴cosα＝＝＝．
∴α＝arccos．
即MA与BC所成角为arccos．
20．解：(1)在△ADE中，y2＝x2＋AE2－2x·AE·cos60°y2＝x2＋AE2－x·AE ①
又S△ADE＝S△ABC＝a2＝x·AE·sin60°x·AE＝2a2 ②
②代入①得：y2＝x2＋()2－2a2(y＞0)
∴y＝(a≤x≤2a)
(2)如果DE是水管y＝≥＝a，
当且仅当x2＝，即x＝a时“＝”成立，故DE∥BC，且DE＝a．
如果DE是参观线路，记f(x)＝x2＋，可知函数在[a，a]上↓，
在[a，2a]上↑，故f(x)max＝f(a)＝f(2a)＝5a2．
∴ymax＝＝a．
即DE为AB中线或AC中线时，DE最长．
21．解：(1)设＝(u，v) 或．
∵＝＋＝(u＋4，v－3)，v－3＞0，∴＝(6，8)．
(2)由(10，5)，LOB方程∶y＝x，
⊙O1方程化为(x－3)2＋(y＋1)2＝10，可求得(3，－1)关于OB对称点(1，3)．
故所求圆方程为(x－1)2＋(y－3)2＝10．
(3)设P(x1，y1)，Q(x2，y2)为抛物线上关于OB对称两点，则
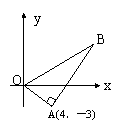
∴x1，x2为方程x2＋x＋＝0两异根．
令△＞0a＞，
故当a＞时，抛物线上总有关于OB对称两点．
22．解：(1)y＝－x3的定义域是R，
y'＝－3x2≤0，∴y＝－x3在R上是单调减函数．
则y＝－x3在[a，b]上的值域是[－b3，－a3]．
由 解得：或 (舍去)或 (舍去)
∴函数y＝－x3属于集合M，且这个区间是[－，]
(2)设g(x)＝＋t，则易知g(x)是定义域[1，＋∞]上的增函数．
g(x)∈M，∴存在区间[a，b][1，＋∞]，满足g(a)＝a，g(b)＝b．
即方程g(x)＝x在[1，＋∞]内有两个不等实根．
[法一]：方程＋t＝x在[1，＋∞]内有两个不等实根，等价于方程x－1＝(x－t)2在[2t，＋∞]内有两个不等实根．
即方程x2－(4t＋4)x＋4t2＋4＝0在[2t，＋∞]内有两个不等实根．
根据一元二次方程根的分布有
解得0＜t≤．
因此，实数t的取值范围是0＜t≤．
[法二]：要使方程＋t＝x在[1，＋∞]内有两个不等实根，
即使方程＝x－t在[1，＋∞]内有两个不等实根．
如图，当直线y＝x－t经过点(1，0)时，t＝，
当直线y＝x－t与曲线y＝相切时，
方程＝x－t两边平方，得x2－(4t＋4)x＋4t2＋4＝0，由△＝0，得t＝0．
因此，利用数形结合得实数t的取值范围是0＜t≤．