2006年高三3月份联考数学试卷(理科)
注意事项:
本试卷分为第Ⅰ卷(选择题)第Ⅱ卷(非选择题)两部分,共8页,满分为150分,考试时间为120分钟。
一. 选择题 : (本大题共10小题, 每小题5分, 共50分. 在每小题给出的四个选项中, 有且只有一项是符合题目要求的,请将答案填写在答卷纸上)
1.复数![]() ,
,![]() ,则
,则![]() 在复平面内的对应点位于( )
在复平面内的对应点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.“两条直线没有公共点”是“这两条直线异面”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.若函数![]() 的图象按向量
的图象按向量![]() 方向平移可得到函数y=sin2
方向平移可得到函数y=sin2![]() 的图象,则
的图象,则![]() 可以是( )
可以是( )
A. (![]() ,0) B. (
,0) B. (![]()
![]() ,0) C. (
,0) C. (![]() ,0) D. (
,0) D. (![]()
![]() ,0)
,0)
4.已知集合![]() ,
,![]() ,则M∩N等于( )
,则M∩N等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.等差数列{an}的前n项和记为Sn,若a3+a7+a11为一个确定的常数,则下列各数中也是常数的是( )
A.S7 B.S11 C.S12 D.S13
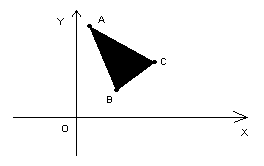 6.已知A(1,6)、B(2,2)、C(4,4),如图所示的坐标平面的可行域内(阴影部分包括周界),若使目标函数
6.已知A(1,6)、B(2,2)、C(4,4),如图所示的坐标平面的可行域内(阴影部分包括周界),若使目标函数![]() 取得最大值的最优解有无穷多个,则a的值等于( )
取得最大值的最优解有无穷多个,则a的值等于( )
A.1 B.4
C.![]() D.6
D.6
7.在圆x2+y2=1上的所有点中,到直线![]() 的距离最大的点的坐标是( )
的距离最大的点的坐标是( )
A.(![]() ) B.(
) B.(![]() ) C.(
) C.(![]() ) D.(
) D.(![]() )
)
8.CD是△ABC的边AB上的高,且![]() ,则( )
,则( )
A.![]() B.
B.![]() 或
或![]()
C.![]() 或
或![]() D.
D.![]() 或
或![]()
9.若![]() 展开式中的第5项是
展开式中的第5项是![]() ,设
,设![]() ,则
,则![]() ( )
( )
 A.1 B.
A.1 B.![]() C.
C.![]() D.
D.![]()
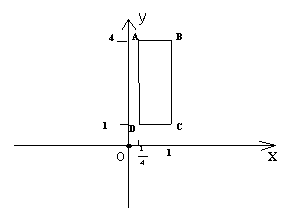
10.已知函数![]() (x∈
(x∈![]() )的值域为[0,2],则点(a,b)的轨迹为图中的( )
)的值域为[0,2],则点(a,b)的轨迹为图中的( )
A.线段AB和BC B.线段AB和AD
C.线段DC和BC D.线段DC和AD
二、填空题:(tx本大题共4小题,每小题4分,共16分.把答案填在答题卷上)
11.已知函数![]() 是一个以6为最小正周期的奇函数,则
是一个以6为最小正周期的奇函数,则![]() (3)= ▲ .
(3)= ▲ .
12.设抛物线![]() 的焦点为F,经过点P(2,1)的直线
的焦点为F,经过点P(2,1)的直线![]() 与抛物线相交于A、B两点且点P恰为AB的中点,则AF+BF= ▲ .
与抛物线相交于A、B两点且点P恰为AB的中点,则AF+BF= ▲ .
13.在半径为6的球面上有A、B、C三点,若AB=2,∠ACB=30°,则球心O到平面ABC的距离为 ▲ .
14.有女学生5名,男学生2名。现从中选4人到4个不同的社区服务,每个社区去1名学生,必须有男学生参加的安排方法种数是 ▲ (用数字作答).
三、解答题(本大题共6个小题,共84分,解答应写出文字说明,证明过程或演算步骤)
15、(本小题满分14分)
已知A、B、C的坐标分别为A(4,0)、B(0.4)、C(3cosα,3sinα)
(Ⅰ)若![]() ,且
,且![]() .求角α的值;
.求角α的值;
(Ⅱ)若![]() .求
.求![]() 的值.
的值.
16、(本小题满分14分)
在数列{an}中,a1=tan![]() ,
,![]() .
.
(Ⅰ)写出a2,a3,a4;
(Ⅱ)猜想{an}的通项公式,并加以证明.
17、(本小题满分14分)
一台仪器每启动一次都随机地出现一个5位的二进制数![]() ,其中A的各位数字中,
,其中A的各位数字中,![]() 出现
出现![]() 的概率为
的概率为![]() ,出现1的概率为
,出现1的概率为![]() .例如:A=10001,其中
.例如:A=10001,其中![]() .记
.记![]() ,当启动仪器一次时,
,当启动仪器一次时,
(Ⅰ)求![]() 的概率;
的概率;
(Ⅱ)求![]() 的概率分布列及
的概率分布列及![]() .
.
18、(本小题满分14分)
如图所示, ![]() VAD是边长为2的等边三角形,ABCD是正方形, 平面VAD
VAD是边长为2的等边三角形,ABCD是正方形, 平面VAD![]() 平面ABCD,E为VC中点.
平面ABCD,E为VC中点.
(Ⅰ)求VC与平面ABCD所成角的余弦值;
(Ⅱ)求D到平面VBC的距离;
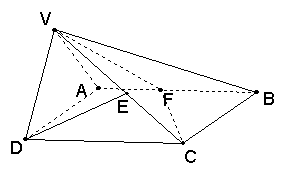 (Ⅲ)在边AB上是否存在一点F,使DE
(Ⅲ)在边AB上是否存在一点F,使DE![]() 面VCF,若存在,求出点F的位置;若不存在,说明理由.
面VCF,若存在,求出点F的位置;若不存在,说明理由.
19、(本小题满分14分)
已知函数![]() (a、b∈R)
(a、b∈R)
(Ⅰ)若x=2是方程![]() =0的一个根,
=0的一个根,![]() 在[0,2]上是增函数,求证:
在[0,2]上是增函数,求证:![]() ≤-2;
≤-2;
(Ⅱ) 设![]() 图象上任意不同两点的连线的斜率为
图象上任意不同两点的连线的斜率为![]() ,若
,若![]() 求
求![]() 的取值范围.
的取值范围.
20、(本小题满分14分)
已知椭圆C的方程为:![]() ,直线
,直线![]() ,直线
,直线![]() ,过椭圆C的右焦点F作直线
,过椭圆C的右焦点F作直线![]() ,使
,使![]() ⊥
⊥![]() 且
且![]() ∩
∩![]() =P.
=P.
(Ⅰ) 若![]() 与
与![]() 的夹角为60°,双曲线E以
的夹角为60°,双曲线E以![]() 与
与![]() 为渐近线,且双曲线E的焦距为4,求双曲线E的方程;
为渐近线,且双曲线E的焦距为4,求双曲线E的方程;
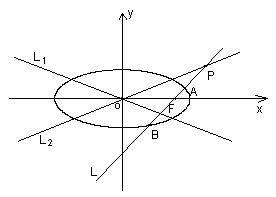 (Ⅱ)若直线
(Ⅱ)若直线![]() 与椭圆C的两个交点为A、B,且A在线段PF上,求
与椭圆C的两个交点为A、B,且A在线段PF上,求![]() 的最大值.
的最大值.
2006高三3月份联考
数学 (理科) 答案
一、选择题 : (本大题共10小题, 每小题5分, 共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | B | A | A | D | C | C | D | A | B |
二、填空题:(本大题共4小题,每小题4分,共16分.把答案填在题中横线上)
11. 0 12. 8 13.![]() 14.720
14.720
三、解答题(本大题共6个小题,共84分,解答应写出文字说明,证明过程或演算步骤)
15.解:![]() …………2分
…………2分
(Ⅰ)![]()
![]() ………………………………………………………………5分
t
………………………………………………………………5分
t
![]() …………………………………………………7分
…………………………………………………7分
(Ⅱ)![]()
![]() ……10分
……10分
![]() …………………12分
…………………12分
![]()
![]()
![]() ……………………………………………………14分
……………………………………………………14分
16.解(Ⅰ)![]() ……5分
……5分
(Ⅱ)猜想:![]() ,下面用数学归纳法证明之: x
,下面用数学归纳法证明之: x
(ⅰ)当![]() 时,显然成立;………………………………………………7分
时,显然成立;………………………………………………7分
(ⅱ)假设![]() 时猜想正确,即
时猜想正确,即![]()
当![]() 时,
时,
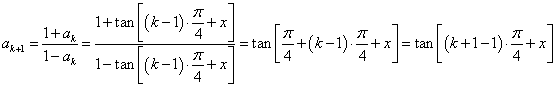 猜想也正确;……………………………………………………………………13分
猜想也正确;……………………………………………………………………13分
由(ⅰ)(ⅱ)知对任何![]() 猜想都正确.………………………………14分
猜想都正确.………………………………14分
17.解(Ⅰ)![]() …………………6分
…………………6分
(Ⅱ)![]()
|
| 1 | 2 | 3 | 4 | 5 |
| P |
|
|
|
|
|
……10分 令![]() ……14分
……14分
18.解:![]() ,取BC中点G
,取BC中点G
(Ⅰ)![]()
![]()
![]() ………………2分
………………2分
![]() …………4分
…………4分
(Ⅱ)设D到面VBC的距离为![]() ,
,
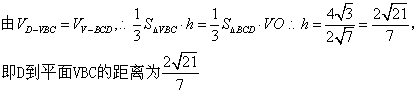 …………8分
…………8分
(Ⅲ)![]()
以O为原点,![]()
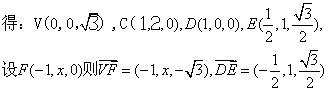 ………………12分
………………12分
 ………………14分
………………14分
19.(Ⅰ)证明∵f(2)=0
∴![]() ∴
∴![]() …………1分
…………1分
由![]() 得
得![]() ,
,![]() …………3分
…………3分
又f(x)在[0,2]上是增函数
∴![]() ≥2 即a≥3…………………………6分
≥2 即a≥3…………………………6分
∴![]() ≤
≤![]() …………7分
…………7分
(Ⅱ)解:设任意不同两点![]() ,且x1≠x2
,且x1≠x2
则![]() ………………………………9分
………………………………9分
![]() ≤
≤![]() …………11分
…………11分
![]() ≤
≤![]() ……………………13分
……………………13分
∴![]() …………………………………………………………………14分
…………………………………………………………………14分
解法二:∵y=f(x)是连续函数.∴总可以在图象上找一点![]() 使以P为切点的切线
使以P为切点的切线
平行图象上任意两点的连线.…………………………………………4分
即![]() ≤
≤![]() <1.…………………………7分
<1.…………………………7分
20.(Ⅰ)![]()
设双曲线E为:![]() (λ≠0)…………………………2分
(λ≠0)…………………………2分
由![]() 得
得![]()
∴双曲线E为:![]() 或
或![]() …………………………4分
…………………………4分
(Ⅱ)设F(c,0),![]() ,
,![]()
由 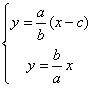 得
得![]() ……………6分
……………6分
过A作AQ⊥直线![]() 于Q点,则
于Q点,则
![]() ,由
,由![]() ……………………8分
……………………8分
而![]() ∴
∴![]()
设![]() ,则
,则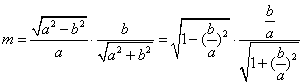 ………10分
………10分
令![]() 则
则![]() …………12分
…………12分
≤![]() ∴
∴![]() ………………………14分
………………………14分
解法二:设![]() F(c,0) ,A (x0,y0),
F(c,0) ,A (x0,y0),![]() …………3分
…………3分
∴ 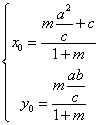 代入椭圆方程得:
代入椭圆方程得: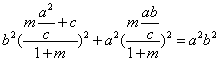
…………………………………………………………6分
![]()
∴![]()
![]() ……………………………………10分
……………………………………10分