2005年高考数学
江苏卷试题及答案
源头学子小屋 
一选择题：本大题共12小题，每小题5分，共60分在每小题给出的四个选项中，只有一项是符合题意要求的
1.设集合
，
，
，则
=（ ）
A．
B．
C．
D．
2.函数
的反函数的解析表达式为
（ ）
A．
B．
C．
D．
3.在各项都为正数的等比数列
中，首项
，前三项和为21，则
=（ ）
A．33 B．72 C．84 D．189
4.在正三棱柱
中，若AB=2，
则点A到平面
的距离为（ ）
A．
B．
C．
D．
5.
中，
，BC=3，则的周长为
（ ）
A．
B．
C．
D．
6.抛物线
上的一点M到焦点的距离为1，则点M的纵坐标是（ ）
A．
B．
C．
D．0
7.在一次歌手大奖赛上，七位评委为歌手打出的分数如下：
，去掉一个最高分和一个最低分后，所剩数据的平均值和方差分别为
（ ）
A．
B．
C．
D．
8.设
为两两不重合的平面，
为两两不重合的直线，给出下列四个命题：①若
，
，则
；②若
，
，
，
，则；
③若，
，则
；④若
，
，
，
，则
其中真命题的个数是 （ ）
A．1 B．2 C．3 D．4
9.设
，则
的展开式中
的系数不可能是 （ ）
A．10 B．40 C．50 D．80
10.若
，则
=
（ ）
A．
B．
C．
D．
11.点
在椭圆
的左准线上，过点P且方向为
的光线经直线
反射后通过椭圆的左焦点，则这个椭圆的离心率为（ ）
A．
B．
C．
D．
12.四棱锥的8条棱代表8种不同的化工产品，有公共点的两条棱代表的化工产品放在同一仓库是危险的，没有公共顶点的两条棱所代表的化工产品放在同一仓库是安全的，现打算用编号为①.②.③.④的4个仓库存放这8种化工产品，那么安全存放的不同方法种数为（ ）
A．96 B．48 C．24 D．0
二.填写题：本大题共6小题，每小题4分，共24分把答案填在答题卡相应位置
13.命题“若
，则
”的否命题为__________
14.曲线
在点
处的切线方程是__________
15.函数
的定义域为__________
16.若
，
,则
=__________
17.已知
为常数，若
，
，则
=__________
18.在中，O为中线AM上一个动点，若AM=2，则
的最小值是__________
三.解答题：本大题共5小题，共66分解答应写出文字说明.证明过程或演算步骤
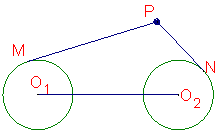19.（本小题满分12分）如图，圆
与圆
的半径都是1，
，过动点P分别作圆.圆的切线PM、PN（M.N分别为切点），使得
试建立适当的坐标系，并求动点P的轨迹方程
20.（本小题满分12分，每小问满分4分）甲.乙两人各射击一次，击中目标的概率分别是
和
假设两人射击是否击中目标，相互之间没有影响；每人各次射击是否击中目标，相互之间也没有影响
⑴求甲射击4次，至少1次未击中目标的概率；
⑵求两人各射击4次，甲恰好击中目标2次且乙恰好击中目标3次的概率；
⑶假设某人连续2次未击中目标，则停止射击问：乙恰好射击5次后，被中止射击的概率是多少？
21.（本小题满分14分，第一小问满分6分，第二.第三小问满分各4分）
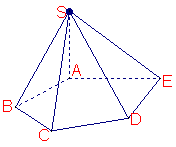如图，在五棱锥S—ABCDE中，SA⊥底面ABCDE，SA=AB=AE=2，
，
⑴求异面直线CD与SB所成的角（用反三角函数值表示）；
⑵证明：BC⊥平面SAB；
⑶用反三角函数值表示二面角B—SC—D的大小（本小问不必写出解答过程）
22.（本小题满分14分，第一小问满分4分，第二小问满分10分）已知
，函数
⑴当
时，求使
成立的
的集合；
⑵求函数
在区间
上的最小值
23.（本小题满分14分，第一小问满分2分，第二.第三小问满分各6分）
设数列的前
项和为
，已知
，且
，其中A.B为常数
⑴求A与B的值；
⑵证明：数列为等差数列；
⑶证明：不等式
对任何正整数
都成立
2005年高考数学江苏卷试题及答案
参考答案
(1)D (2)A (3)C (4)B (5)D (6)B (7)D (8)B (9)C (10)A (11)A (12)B
（13）若，则
（14）
（15）
（16）-1
（17）2 （18）-2
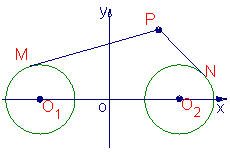（19）以的中点O为原点，所在的直线为x轴，建立平面直角坐标系，则（-2，0），（2，0），
由已知
，得
因为两圆的半径均为1，所以
设
，则
，
即
，
所以所求轨迹方程为（或
）
（20）（Ⅰ）记“甲连续射击4次，至少1次未击中目标”为事件A1，由题意，射击4次，相当于4次独立重复试验，故P（A1）=1- P（
）=1-
=
答：甲射击4次，至少1次未击中目标的概率为；
(Ⅱ) 记“甲射击4次，恰好击中目标2次”为事件A2，“乙射击4次，恰好击中目标3次”为事件B2，则
，
，
由于甲、乙设计相互独立，故
答：两人各射击4次，甲恰好击中目标2次且乙恰好击中目标3次的概率为
；
（Ⅲ）记“乙恰好射击5次后，被中止射击”为事件A3，“乙第i次射击为击中”
为事件Di，（i=1，2，3，4，5），则A3=D5D4
，且P（Di）=
，由于各事件相互独立，
故P（A3）= P（D5）P（D4）P（）=×××（1-×）=
，
答：乙恰好射击5次后，被中止射击的概率是
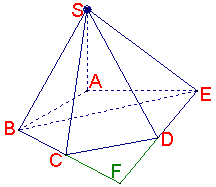（21）（Ⅰ）连结BE，延长BC、ED交于点F，则∠DCF=∠CDF=600，
∴△CDF为正三角形，∴CF=DF
又BC=DE，∴BF=EF因此，△BFE为正三角形，
∴∠FBE=∠FCD=600，∴BE//CD
所以∠SBE（或其补角）就是异面直线CD与SB所成的角
∵SA⊥底面ABCDE，SA=AB=AE=2，
∴SB=
，同理SE=，
又∠BAE=1200，所以BE=
，从而，cos∠SBE=
，
∴∠SBE=arccos
所以异面直线CD与SB所成的角是arccos
(Ⅱ) 由题意，△ABE为等腰三角形，∠BAE=1200，
∴∠ABE=300，又∠FBE =600，
∴∠ABC=900，∴BC⊥BA
∵SA⊥底面ABCDE，BC
底面ABCDE，
∴SA⊥BC，又SA
BA=A，
∴BC⊥平面SAB
（Ⅲ）二面角B-SC-D的大小
（22）（Ⅰ）由题意，
当
时，由
，解得
或
；
当
时，由
，解得
综上，所求解集为
(Ⅱ)设此最小值为
①当
时，在区间[1，2]上，
，
因为
，
，
则
是区间[1，2]上的增函数，所以
②当
时，在区间[1，2]上，
，由
知
③当
时，在区间[1，2]上，
若
，在区间（1，2）上，
，则是区间[1，2]上的增函数，
所以
若
，则
当
时，，则是区间[1，
]上的增函数，
当
时，
，则是区间[，2]上的减函数，
因此当时，或
当
时，
，故，
当
时，
，故
总上所述，所求函数的最小值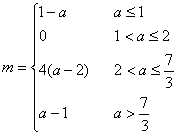
（23）（Ⅰ）由已知，得
，
，
由
，知
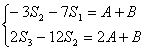，即
解得
.
(Ⅱ) 由（Ⅰ）得
①
所以 
②
②-①得 
③
所以 
④
④-③得 
因为 
所以 
因为 
所以 
所以 
，
又 
所以数列
为等差数列
（Ⅲ）由(Ⅱ) 可知，
，
要证
只要证 
，
因为 
，
，
故只要证 
，
即只要证 
，
因为 
所以命题得证