洪泽县中学2006届高三周练06.3.26
数学试卷
一. 选择题:(题共12小题, 每小题5分,共60分)
1. 已知集合![]() ,则必有
( )
,则必有
( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
2. 不等式![]() 的解集是
( )
的解集是
( )
A. ![]() B.
B.
![]() C.
C. ![]() D.
D. ![]()
3. 函数![]() 的最小正周期是 ( )
的最小正周期是 ( )
A. ![]() B.
B.
![]() C. 2
C. 2![]() D. 4
D. 4![]()
4. 若![]() ,
, ![]() , 且 a∥b, 则x的值为 ( )
, 且 a∥b, 则x的值为 ( )
A. ![]() B
.
B
. ![]() C. -6
D. 6
C. -6
D. 6
5. 下列函数中, 在区间![]() 上为减函数的是
( )
上为减函数的是
( )
A. ![]() B.
B.
![]() C.
C. ![]() D.
D. ![]()
6. 如果![]() 则
则![]() 的最小值是 ( )
的最小值是 ( )
A. 2
B. ![]() C.
C.
![]() D.
D. ![]()
7、从{1,2,3,4,………,20 }中任取3个不同的数,使这三个数仍成等差数列,则这样的等差数列最多有 ( )
(A)90个 (B)120个 (C)180个 (D)200个
8. 两位同学一起去一家单位应聘, 面试前单位负责人对他们说:“我们要从面试的人中招聘3人,你们俩同时被招聘进来的概率是![]() ”.根据这位负责人的话可以推断出参加面试的人数为 ( )
”.根据这位负责人的话可以推断出参加面试的人数为 ( )
A. 21 B. 35 C. 42 D. 70
9. 设l1、 l2为直线,
![]() 为平面.下面四个命题中, 正确的是
(
)
为平面.下面四个命题中, 正确的是
(
)
![]()
![]()
![]()
C. l1、l2与所成的角相等![]() l1∥l2
l1∥l2
10. 离心率为黄金比![]() 的椭圆称为“优美椭圆”. 设
的椭圆称为“优美椭圆”. 设![]()
![]() 是优美椭圆, F、A分别是它的左焦点和右顶点, B是它的短轴的一个端点, 则
是优美椭圆, F、A分别是它的左焦点和右顶点, B是它的短轴的一个端点, 则![]() 等于
( )
等于
( )
A. 60° B. 75° C. 90° D. 120°
11. 设函数![]() 图象的一条对称轴方程为
图象的一条对称轴方程为![]() , 则直线
, 则直线![]() 的倾斜角为
( )
的倾斜角为
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
12、定义在R上的函数y=f(x),在(-∞,![]() )上是增函数,且函数y=f(x+
)上是增函数,且函数y=f(x+![]() )是偶函数,当x1<
)是偶函数,当x1<![]() ,x2>
,x2>![]() 且
且![]() 时,有( )
时,有( )
(A) f(2![]() - x1)> f(2
- x1)> f(2![]() - x2) (B) f(2
- x2) (B) f(2![]() - x1)= f(2
- x1)= f(2![]() - x2)
- x2)
(C) f(2![]() - x1)< f(2
- x1)< f(2![]() - x2) (D) -f(2
- x2) (D) -f(2![]() - x1)< f(x2-2
- x1)< f(x2-2![]() )
)
二. 填空题:(本大题共6小题;每小题4分,共24分)
13. 在![]() 的展开式中, 第4项是常数项, 则n= .
的展开式中, 第4项是常数项, 则n= .
14. 如果直线沿向量![]() 则直线l的斜率是__________.
则直线l的斜率是__________.
15. 若曲线![]() 在点P处的切线平行于直线
在点P处的切线平行于直线![]() , 则点P的坐标为
.
, 则点P的坐标为
.
16.圆x2+y2=2上到直线x-y-4=0距离最近的点的坐标是_________.
17. 将容量为100的样本数据按从小到大的顺序分成8个组,如下表:
|
则第六组的频率为 .
18. 半球内有一内接正方体, 正方体的一个面在半球的底面圆内. 若正方体的棱长为![]() , 则半球的体积为 .
, 则半球的体积为 .
三. 解答题:(本大题5小题,共66分)
19. (本题12分) 已知向量![]() ,
, ![]() .
.
(1) 当![]() 时, 求
时, 求![]() 的值; (2) 求函数
的值; (2) 求函数![]() 的值域.
的值域.
解: ![]()
![]()
![]() …… (3分)
…… (3分)
(1)![]() ∴
∴![]() ……(4分) 又
……(4分) 又![]()
![]() ∴
∴![]() ……(7分)
……(7分)
(2)![]() ……(8分)
……(8分)
![]() ……(10分)
……(10分)
 ∴
∴![]() .……(12分)
.……(12分)
20.(本题12分)已知: 如图, 长方体AC1中, 棱AB=BC=3, 棱BB1=4, 连结B1C, 过点B作B1C的垂线交CC1于点E, 交B1C于点F.
(1) 求证: A1C![]() 平面EBD;
平面EBD;
(2) 求点A到平面A1B1C的距离;
(3) 求ED与平面A1B1C所成角的大小.
解: (1)连结AC.在长方体AC1中, A1C在底面ABCD上的射影为AC, AC⊥BD,
∴AC1⊥BD. ……(2分)
在长方体AC1中, A1C在平面BB1C1C上的射影为B1C,B1C⊥BE, ∴A1C⊥BE. ……(3分)
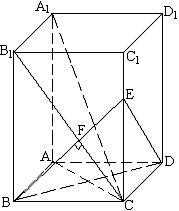 又BD
又BD![]() BE=B, ∴A1C⊥平面EBD. …… (4分)
BE=B, ∴A1C⊥平面EBD. …… (4分)
(2) ∵BF⊥B1C, BF⊥AB1, B1C![]() A1B1=B1,
A1B1=B1,
∴BF⊥平面A1B1C1, ……(5分)
又∵A1B1∥AB, A1B1![]() 平面A1B1C,AB
平面A1B1C,AB![]() 平面A1B1C,
平面A1B1C,
∴AB∥平面A1B1C, 点A到平面A1B1C的距离即为点
B到平面A1B1C距离, 也就是BF. …… (7分)
在△B1BC中, 易知![]()
![]() ,
,
点A到平面A1B1C的距离为![]() .…… (8分)
.…… (8分)
(3)连结A1D、FD. 由(2)知BE⊥平面A1B1C,
即BE⊥平面A1B1CD,
∴∠EDF为ED与平面A1B1C所成的角. ……(9分)
矩形B1BCC1中, 易求得B1F=![]() , CF=
, CF=![]() , EF=
, EF=![]() EC=
EC=![]()
又在Rt△CDE中, ![]() ,……(11分)
,……(11分)
![]() 即ED与平面A1B1C所成角为
即ED与平面A1B1C所成角为![]() .……(12分)
.……(12分)
21.(14分)某渔业公司年初用98万元购买一艘捕鱼船,第一年各种费用为12万元,以后每年都增加4万元,每年捕鱼收益50万元.
(1)问第几年开始获利? (2)若干年后,有两种处理方案:
方案一:年平均获利最大时,以26万元出售该渔船
方案二:总纯收入获利最大时,以8万元出售该渔船.问哪种方案合算.
解析:(1)由题意知,每年的费用以12为首项,4为公差的等差数列.
设纯收入与年数n的关系为f(n),则
![]() …
…![]() .……… 2分
.……… 2分
由题知获利即为f(n)>0,由![]() ,得
,得![]()
![]() .
.
∴ 2.1<n<17.1.而n![]() N,故n=3,4,5,…,17 ……………5分
N,故n=3,4,5,…,17 ……………5分
.∴ 当n=3时,即第3年开始获利.…………………6分
(2)方案一:年平均收入![]() .
.
由于![]() ,当且仅当n=7时取“=”号.…………8分
,当且仅当n=7时取“=”号.…………8分
∴ ![]() (万元).……………9分
(万元).……………9分
即第7年平均收益最大,总收益为12×7+26=110(万元).………10分
方案二:f(n)=![]() +40n-98=-2
+40n-98=-2![]() +102.
+102.
当n=10时,f(n)取最大值102,总收益为102+8=110(万元).………12分
比较如上两种方案,总收益均为110万元,而方案一中n=7,故选方案一.…14分
22.(本题满分14分)已知正方形ABCD的外接圆方程为 x2+y2-24x+a=0 (a<144),正方形一边CD所在直线的方向向量为(3,1),
(1)求正方形对角线AC与BD所在直线的方程;
(2)若顶点在原点焦点在x轴的抛物线E经过正方形在x轴上方的两个顶点A、B,求抛物线E的方程。
(3) 设点N(1,2),过点(5,-2)的直线与抛物线E交于另外两点S、T.试判断三角形NTS的形状?(锐角、钝角或直角三角形)并证明之.
解(1)由![]() 可知圆心M的坐标为(12,0),
依题意:
可知圆心M的坐标为(12,0),
依题意: ![]() ,
, ![]() ,
,
MA、 MB的斜率k满足: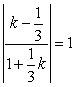 ,解得:
,解得:![]()
![]() …… (2分)
…… (2分)
∴所求AC方程为:x+2y-12=0 BD方程为:2x-y-24=0 ……………(4分)
(2) 设MB、 MA的倾斜角分别为θ1,θ2,则tanθ1=2,tanθ2=![]() ,
,
设圆半径为r,则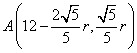 ,
,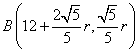 …………(6分)
…………(6分)
再设抛物线方程为y2=2px (p>0),由于A, B两点在抛物线上,
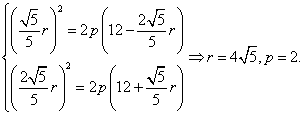
得抛物线方程为y2=4x. ……………( 9分)
(3)【证明】设T(t2,2t)、S(s2,2s),s≠t,s≠1,t≠1,则直线ST的方程为
![]()
化简得2x-(s+t)y+2st=0.由于直线ST过点(5-2),故2×5-(s+t)(-2)+2st=0,
即(s+1)(t+1)=-4. ……………(11分)
因此![]()
所以∠TNS=90°.从而△NTS是直角三角形. …………… (14分)
(23) (本小题满分14分)已知函数![]() 在区间[n,m]上为减函数,记m的最大值为m0,n的最小值为n 0,且有m0- n 0=4.
在区间[n,m]上为减函数,记m的最大值为m0,n的最小值为n 0,且有m0- n 0=4.
(1)求m0,n 0的值以及函数![]() 的解析式;
的解析式;
(2)已知等差数列{xn}的首项![]() ,公差
,公差![]() .又过点
.又过点![]() 的直线方程为
的直线方程为![]() 试问:在数列{xn}中,哪些项满足
试问:在数列{xn}中,哪些项满足![]() ?
?
(3)若对任意![]() ,都有
,都有![]() 成立,求a的最小值.
成立,求a的最小值.
解(1)![]() 由题意可知
由题意可知![]() 为方程
为方程![]() 的两根
的两根
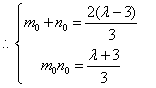 其中
其中![]()
![]()
![]() 解得
解得![]()
![]()
![]()
(2)由(1)得A(0,5),B(1,-6),![]() 6/
6/
![]()
又由题得![]() 可解得
可解得![]() 或
或![]()
![]() 当
当![]() 或
或![]() 时,满足题意 (3)
时,满足题意 (3)
![]()
![]() 由题意,
由题意,![]() 恒成立,即
恒成立,即![]() 恒成立
恒成立
![]()
要使![]() 恒成立,只要
恒成立,只要![]() 成立,即只要
成立,即只要![]() 成立
成立
![]() 的最小值为1
的最小值为1
一. 选择题(每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | B | C | C | D | C | C | A | D | C | B | A |
二. 填空题(每小题4分,共16分)
13. 18 ; 14. ![]() ; 15.
; 15. ![]() ;
;
16(1,—1) 17.0.15 18. ![]() .
.