2005—2006学年度重 庆 一 中高三年级阶段测试
数 学 试 卷（理）
一、选择题：（本大题共12小题，每小题5分，共50分，在每小题给出的四个选项中，只
有一项是符合题目要求的.）
1．设p、q是两个命题，则“复合命题p或q为真，p且q为假”的充要条件是 （ ）
A．p、q中至少有一个为真 B．p、q中至少有一个为假
C．p、q中有且只有一个为真 D．p为真，q为假
2．设向量
（ ）
A．60° B．30° C．75° D．45°
3．已知全集
，则 （ ）
|
|
|
B．
C． N=M D． N M
4．已知等差数列
的前n项和为
（ ）
A．
B．
C．
D．
5．已知函数
图像的一条对称轴是 （ ）
A．
B．
YCY C．
D．
6．设
是互相垂直的单位向量，且
，则
等于（ ）
A．－1 B．－2 C．1 D．2
7．已知函数
的反函数
的图象对称中心是（－1，3），则实数a等于
（ ）
A．2 B．1 C．－4 D．－2
8．定义在R上的偶函数
上递减，且
，则满足
的
的集合为 （ ）
A．
B．
C．
D． 
9．若关于的方程
只有一个实根，则实数
的取值为 （ ）
A．
B．
C．
YCY D．
10．已知
时，不等式
恒成立，则a的取值范围是（ ）
A．
B．
YCY C．
D．
第Ⅱ卷（非选择题 共90分）
二、填空题：本大题共4小题，每小题4分，共24分
11．已知
的夹角为
，要使
垂直，则
.
12．函数
的定义域是
则其值域是
.
|
，则前9项的和
等于 .
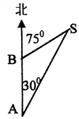
14．如图，一艘船上午9∶30在A处测得灯塔S在它的北偏东30°处，
之后它继续沿正北方向匀速航行，上午10∶00到达B处，此时又测
得灯塔S在它的北偏东75°处，且与它相距
mile. 此船的航
速是 n mile/h.
15．不等式
和不等式
的解集相同，则a+b=
.
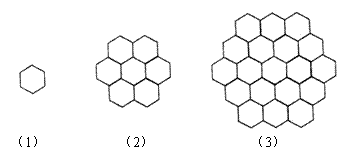16．单个的蜂巢近似一个正六边形.
如下图，这是一组蜂巢的图形：
设第（1）图有一个蜂巢，第（2）图有7个蜂巢，第三图有19个蜂巢，按此规律，
第（n）图共有 个蜂巢.
三、解答题：本大题共6小题，共76分，解答应写出文字说明、证明过程或演算步骤.
17．（本小题满分12分）已知函数
（1）求实数a，b的值；
（2）求函数
的最大值及取得最大值时x的值.
18．（本小题满分13分）已知
之间有关系式
（1）用k表示；
（2）求的最小值，并求此时
的夹角
的大小.
19．（本小题满分13分）解关于x的不等式：
20．（本小题满分12分）
随着机构改革开作的深入进行，各单位要减员增效，有一家公司现有职员2a人
（140＜2a＜420，且a为偶数
，每人每年可创利b万元. 据评估，在经营条件不变的前
提下，每裁员1人，则留岗职员每人每年多创利0.01b万元，但公司需付下岗职员每人
每年0.4b万元的生活费，并且该公司正常运转所需人数不得小于现有职员的
，为获得
最大的经济效益，该公司应裁员多少人？
21．（本小题满分13分）已知函数是定义在R上的奇函数，当
时，
（1）求的解析式；
（1）试确定函数
的单调区间，并证明你的结论；
（2）若
，证明：
22．（本小题满分14分）
已知一列非零向量
满足：
（1）证明：
是等比数列；
（2）求向量
；
（3）设
中所有与
共线的向量按原来的顺序排成一列，记
为
令
为坐标原点），求点列
的极限
点B的坐标.
（注：若点Bn坐标为
，则称点
为点列的极
限点.）
数学参考答案
一、选择题：本题考查基本知识和基本运算，每小题5分，满分50分.
1.C 2.D 3.B 4.D 5.C 6.A 7.A 8.B 9.D 10.B
二、填空题：本题考查基本知识和基本运算，每小题4分，满分24分.
11．2； 12．
； 13．99； 14．32； 15．
； 16．
三、解答题：
17．（本题满分12分）
（1）函数
；
（2）
所以当
的最大值为12.
18．（本题满分13分）
解：（1）由
.
（2）
的最小值为
此时的夹角为60°.
19．（本题满分13分）
解：原不等式等价于
当
（2）当
不等式即为
当
时，
，于是当
,
综上所述：
；
当
20．（本题满分12分）解：设裁员x人，可获得的经济效益为y万元，则
依题意 
（1）当
取到最大值；
（2）当
取到最大值；
综上所述，当
21．（本题满分13分）
解：（1）若
（1）若
是奇函数，
（2）设
上的任意两个实数，且
则
当
，
上为减函数.
同理，当
上为增函数.
（3）
同号，先证明
均为正数
是增函数，由
且
.
若均为负数，
，已知
上是增
函数，
22．（本题满分13分）
解：（1）
首项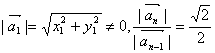
为常数，
是等比数列.
（2）
，
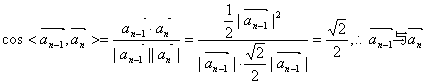的夹角为
.
（3）
，
，
一般地，
用数学归纳法易证
成立.
……………………11分，
设
；
，
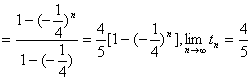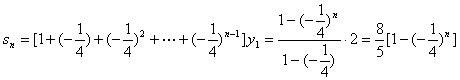∴极限点B的坐标为