高考应用题失分原因及对策
吴县中学 周永峰
从1993年高考数学试题引入应用问题以来,应用题成了每年必考内容并且所占比重越来越大。但它也是令学生头痛不已的问题,往往花了不少时间和精力却得不到一个理想的分数。那么导致应用题失分严重的原因是什么?如何改变这一状况呢?本文结合历年高考中出现的应用题,针对学生解题思维过程加以分析。
一、近几年高考应用题情况表
| 年份 | 题号 | 分值 | 问题情况 | 建模类型 |
| 1993 | 17,22 | 4,4 | 贺卡分配,水池造价 | 排列组合,函数 |
| 1994 | 5,10,20 | 4,4,4 | 细菌繁殖,任务分配,物理测量 | 数列,排列组合,函数 |
| 1995 | 24 | 12 | 淡水养鱼 | 函数 |
| 1996 | 23 | 10 | 耕地粮食 | 方程不等式 |
| 1997 | 22 | 12 | 汽车运费 | 函数 |
| 1998 | 11,22 | 5,12 | 分配方案,污水处理 | 排列组合,函数不等式 |
| 1999 | 16,22 | 5,12 | 作物间作,机器原理 | 排列组合,数列 |
| 2000 | 6,13,21 | 5,4,12 | 税收,分配方案,市场经济 | 函数,排列,函数 |
二、失分原因
1.题意理解不清晰
高考中的应用题都是社会生活实际问题通过一定加工、省略了一些干扰因
素而编写出来的。一般文字繁多、叙述冗长,文字语言、符号语言、图形语言相互交织,这就对学生的阅读理解和逻辑思维能力提出了一定的要求,但学生往往由于生活阅历的积累不够对应用题的背景感觉陌生,从而产生畏难情绪。
如98年第22题中的“沉淀箱”“杂质的质量分数”、99年第22题中的“冷轧机”“减薄率”“疵点”“轧棍”等专业名词令学生望而生畏感觉无从下手。
2.建模技能不过硬
解应用题最关键的是将实际问题数学化,即在分析联想的基础上将实际问题转化为数学问题。但由于应用题中往往数据比较多,关系比较复杂,学生无法将题中条件一一联系起来,准确列出关系式。
如96年第23题涉及“耕地面积10000公顷”“10年”“粮食单产增加22%”“人均粮食占有量提高10%”“人口年增长率1%”数据一多,学生往往找不到各数据之间的关系。
3.解题思维不严密
应用题转化为数学模型后,所需数学知识和数学方法均为基本知识和基本方法,难度不大,但应特别注意题目设置的限制条件(有时是隐蔽的),忽略变量或常量的取值范围也是导致失分的一个重要原因。
如97年第22题忽略最高车速C千米/小时这一条件就会导致直接利用基本不等式而不讨论V能否取到![]() 。98年第22题中列出
。98年第22题中列出![]() 后,不能按实际的题标出k>0就不容易想到将求y的最小值转化为求ab的最大值了。
后,不能按实际的题标出k>0就不容易想到将求y的最小值转化为求ab的最大值了。
三、对策
1.注重知识积累,加强阅读理解
近年高考应用题的基本原则是:靠近课本、贴近生活、联系实际。因此我
们要指导学生留心观察周围的现实世界、拓宽自己的知识面,对一些常识性的概念如“复利”“利润”“双循环、单循环”等都应熟知。另外在读题时应注意提炼“主题词”,砍去一些次要的字词句,突出问题实质。如98年第22题的“主题词”为:无盖长方体长为a,宽为3,高为b,质量分数与ab成反比,制箱材料60平方米,质量分数最小,这就清楚地告诉我们本题是用固定数量的材料制造沉淀箱处理污水的最值问题。
2.掌握语言转化,熟悉常见模型
高考应用题中条件、结论的表达涉及文字、符号、图形、表格等多种形式。在平时的教学中应注意让学生进行各种语言转化的训练,同时帮助学生归纳高考应用题中常用模型(主要有函数模型、方程不等式模型、数列模型、排列组合模型、几何模型等)让学生做到心中有数。
3.加强算法算理的训练,培养思维的严密性。
应用题通过建模形成纯数学问题,平时对数学基础知识基本技能的训练,能够使学生顺利得到纯数学问题的解答。另外平时多注意正误辨析,分类讨论等也能帮助学生形成严密的思维,减少解题时不必要的障碍和无谓失分。
学生应用意识的培养能力的提高不是简单地靠高三复习能一蹴而就的,应用问题的解决除需要扎实的数学基本知识、方法还要具有良好的阅读能力、建模能力和良好的心理素质。因此应用教学应贯穿于整个数学教学的始终,一方面,教师应注意结合教材加强数学知识应用的渗透,另一方面教师要引导学生解决身边的实际问题,从根本上提高学生分析、解决实际问题的能力。
四、练习
1.一批救灾物资用26辆汽车从某市以V公里/小时的速度匀速运往灾区,已知两地公路线长400公里,为了安全,两辆汽车的间距不小于![]() 公里,那么这批物资全部运达灾区,最少需要________小时。
公里,那么这批物资全部运达灾区,最少需要________小时。
2.某工厂产量第二年增长率为a,第三年增长率为b,这两年平均增长率为x,则x与![]() 的大小关系是__________。
的大小关系是__________。
3.一办公大楼共23层,现每层派一人集中到第k层开会,则当k=______时这23位参加会议的人员上下楼梯所走的路程总和最小。
4.一条铁路原有m个车站,为适应客运的需要新增设了n个车站(n≥2),则客运车票增加了58种,那么原有车站________个。
5.降水量是指水平地面上单位面积所降雨水的深度,现用上口直径为38cm,下底直径为24cm,高为70cm的圆台形量桶来测量降水量,如果在一次降雨过程中测得桶中的雨水正好是桶深的![]() ,那么这次降水量是______mm(精确到1mm)。
,那么这次降水量是______mm(精确到1mm)。
6.一辆卡车要通过跨度为8米,拱高为4米的抛物线型隧道(从隧道正中通过)为保证安全车顶距隧道顶部至少应有0.5米距离。如果卡车宽为1.6米,则卡车的限高为________米(精确到0.01米)
7.某工厂生产某产品所需要的费用为P元,而卖出X吨的价格为每吨Q元。已知P=1000+5x+![]() ,Q=
,Q=![]() 。若生产出的产品能够全部卖掉,且在产量为150吨时利润最大,此时每吨价格为40元,求实数a、b的值。
。若生产出的产品能够全部卖掉,且在产量为150吨时利润最大,此时每吨价格为40元,求实数a、b的值。
8.甲、乙两地相距100公里,在甲地有60吨货物要运到乙地,已知汽车的耗油量Q(公升)与路程S(公里)、汽车的载重量W(吨)之间满足Q=S·(0.004W2+0.2),问派一辆载重量多少吨的汽车往返运送,可使总耗油量最小?(每次送货载重量相同)
9.有一个人在草地上散步,开始时从O处出发,向正东行走,每走一公里后便向左转弯一个角度θ,问他走过N公里后,离出发点的直线距离是多少?如果θ=![]() ,能回到出发点吗?
,能回到出发点吗?
10.某企业生产的甲产品使企业1999年盈利a万元,预计从2000年起,20年内甲产品的盈利将每年比上一年减少![]() ,为此企业开发了新产品乙,并将于2000年投入市场,预计乙产品在第一年为企业盈利b万元,在以后的20年内每年的盈利都比上一年增长
,为此企业开发了新产品乙,并将于2000年投入市场,预计乙产品在第一年为企业盈利b万元,在以后的20年内每年的盈利都比上一年增长![]() ,若b=
,若b=![]() a,问企业在今后20年内哪一年盈利最少,最少盈利多少万元?
a,问企业在今后20年内哪一年盈利最少,最少盈利多少万元?
五、简解
1.10 2.x≤![]() 3.12
4.14 5.135
6.3.34
3.12
4.14 5.135
6.3.34
7.解:利润=Qx―P=x(a+![]() )―(1000+5x+
)―(1000+5x+![]() x2)=(
x2)=(![]() )x2+(a―5)x―1000
)x2+(a―5)x―1000
![]() 依题意 ―
依题意 ―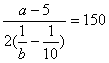
a+![]()
∴a=45, b=―30
8.解题汽车载重量为x吨。则总耗油量
y=![]() [100(0.004x2+0.2)+100×0.2]
[100(0.004x2+0.2)+100×0.2]
=![]() =24x+
=24x+![]() ≥480
≥480
当且仅当24x=![]() 而x=10时y最小。
而x=10时y最小。
∴应派一辆载重量为10吨的汽车运送货物。
9.解:z1=1,z2=1+(cosθ+isinθ),z3=1+(cosθ+isinθ)+(cos2θ+isin2θ)……
zn=![]() d=zn=
d=zn=![]()
如果θ=![]() ,则当n=6时zn=0,即能回到出发点。
,则当n=6时zn=0,即能回到出发点。
10.解企业第n年盈利an=(1―![]()
=![]() ≥2a·
≥2a·![]()
当且仅当![]() 即n=4时有最小值2a
即n=4时有最小值2a![]() .
.