高考模拟试题

2006届高三第四次月考

数 学 试 题（理科）

一．选择题（每个小题只有一个选项符合题意，每小题5分，共60分）

1．设P、Q为两个非空实数集合，定义集合P+Q=

　　　 ，则P+Q中元素的个数是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

A．9　 　　　　 B．8　　 　　　　C．7　　　 　　　　  D．6

2．为了得到函数的图象，只需把函数上所有点

　 （A）向右平移3个单位长度，再向下平移1个单位长度

　 （B）向左平移3个单位长度，再向下平移1个单位长度

　 （C）向右平移3个单位长度，再向上平移1个单位长度

　 （D）向左平移3个单位长度，再向上平移1个单位长度

3．“m=”是“直线(m+2)x+3my+1=0与直线(m－2)x+(m+2)y－3=0相互垂直”的

　　（A）充分必要条件　　　　（B）充分而不必要条件

　　（C）必要而不充分条件　　（D）既不充分也不必要条件

　4．若，且，则向量与的夹角为

　　（A）30°　 （B）60°　　 （C）120°　 （D）150°

　5．从原点向圆 x²＋y²－12y＋27=0作两条切线，则这两条切线的夹角的大小为

　　 （A）　 （B）　　 （C）　　 （D）

6．对任意的锐角α，β，下列不等关系中正确的是

　　（A）sin(α+β)>sinα+sinβ　　（B）sin(α+β)>cosα+cosβ

　　（C）cos(α+β)<sinα＋sinβ　 （D）cos(α+β)<cosα＋cosβ

7．在正四面体P－ABC中，D，E，F分别是AB，BC，CA的中点，下面四个结论中不成立的是

　　（A）BC//平面PDF　　　　　 （B）DF⊥平面PA E

　　（C）平面PDF⊥平面ABC　　　（D）平面PAE⊥平面 ABC

8．五个工程队承建某项工程的五个不同的子项目，每个工程队承建1项，其中甲工程队不能承建1号子项目，则不同的承建方案共有

（A）种　　　（B）种　　　（C）种　　　（D）种

9．对任意实数a，b，c，给出下列命题：

　　　 ①“”是“”充要条件；　②“是无理数”是“a是无理数”的充要条件③“a>b”是“a²>b²”的充分条件；④“a<5”是“a<3”的必要条件.

　　　 其中真命题的个数是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　　 A．1　　　　　　　　　　　　B．2　　　　　　　　　　　　C．3　　　　　　　　　　　　D．4

10．已知向量a=（－2，2），b=（5，k）.若a+b不超过5，则k的取值范围是　　　　

　　　 A．[－4，6]　　　　　　 B．[－6，4]　　　　　　 C．[－6，2]　　　　　　 D．[－2，6]

11．函数的图象大致是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

12．．把一同排6张座位编号为1，2，3，4，5，6的电影票全部分给4个人，每人至少分1张，至多分2张，且这两张票具有连续的编号，那么不同的分法种数是　　

　　　 A．168　　　　　　　　　　 B．96　　　　　　　　　　　 C．72　　　　　　　　　　　D．144

二、填空题：本大题共4小题，每小题4分，共16分.

13．函数的定义域是　　 　　　　.

14．的展开式中整理后的常数项等于　　　　  .

15．函数的最小正周期与最大值的和为　　　　　　  .

16．某实验室需购某种化工原料106千克，现在市场上该原料有两种包装，一种是每袋35千克，价格为140元；另一种是每袋24千克，价格为120元. 在满足需要的条件下，最少要花费　　　　  元.

三、解答题：（本大题共6小题，共74分。解答应写出文字说明，证明过程或演算步骤。）

17．（本小题共12分）

　　已知=2，求

（I）的值；　 （II）的值．

18．（本小题共12分）

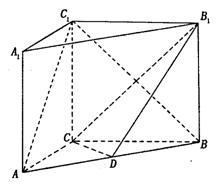
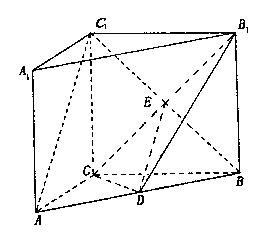
 如图, 在直三棱柱ABC－A₁B₁C₁中，AC＝3，

BC＝4， ∠A₁B₁C₁＝90º

AA₁＝4，点D是AB的中点，

　（I）求证：AC⊥BC₁；

　（II）求证：AC ₁//平面CDB₁；

　（III）求异面直线 AC₁与 B₁C所成角的余弦值．

19．（本小题满分12分）

数列{a_n}的前n项和为S_n，且a₁=1，，n=1，2，3，……，求

　 （I）a₂，a₃，a₄的值及数列{a_n}的通项公式；

　 （II）的值.

20．（本小题满分12分）

甲、乙两人在罚球线投球命中的概率分别为，投中得1分，投不中得0分.

（Ⅰ）甲、乙两人在罚球线各投球一次，求两人得分之和ξ的数学期望；

（Ⅱ）甲、乙两人在罚球线各投球二次，求这四次投球中至少一次命中的概率；

21．（本小题满分12分）

已知函数的图象过点P（0，2），且在点M（－1，f（－1））处的切线方程为.

　 求函数的解析式；

22．（本小题满分14分）

　　　 设A、B是椭圆上的两点，点N（1，3）是线段AB的中点，线段AB的垂直平分线与椭圆相交于C、D两点.

　 （Ⅰ）确定的取值范围，并求直线AB的方程；

（Ⅱ）试判断是否存在这样的，使得A、B、C、D四点在同一个圆上？并说明理由.

数学试题参考答案及评分标准

一、选择题（本大题共12小题，每小题5分，共60分）

　　 1． B　　　2．A　　 3．B　　 4．C　　　5．B　　6．D

7．C　　　8．B　　 9．B　　 10．C　　 11．D　 12．D

二、填空题：本题考查基本知识和基本运算，每小题4分，满分16分.

13．　　14．38　　　15．　　　 16．500

三、解答题（本大题共6小题，共80分）

　 17．（12分）解：（I）∵ tan=2, ∴ ;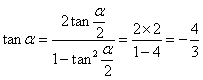

所以=；

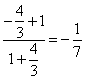（II）由(I), tanα=－, 所以==.

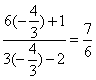18．（共14分）

（I）直三棱柱ABC－A₁B₁C₁，底面三边长AC=3，BC=4AB=5，

∴ AC⊥BC，且BC₁在平面ABC内的射影为BC，∴ AC⊥BC₁；

（II）设CB₁与C₁B的交点为E，连结DE，∵ D是AB的中点，E是BC₁的中点，∴ DE//AC₁，

∵ DE平面CDB₁，AC₁平面CDB₁，∴ AC₁//平面CDB₁；

（III）∵ DE//AC₁，∴ CED为AC₁与B₁C所成的角，

在△CED中，ED=AC ₁=，CD=AB=，CE=CB₁=2，

∴ ，

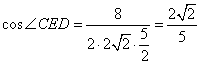∴ 异面直线 AC₁与 B₁C所成角的余弦值.

19.（12分）

解：（I）由a₁=1，，n=1，2，3，……，得

，，，

由（n≥2），得（n≥2），

又a₂=，所以a_n=(n≥2),

∴ 数列{a_n}的通项公式为；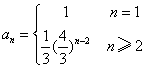

（II）由（I）可知是首项为，公比为项数为n的等比数列，∴=.

20．本小题主要考查概率的基本知识，运用数学知识解决问题的能力，以及推理和运算能力. 满分12分.

　　解：（Ⅰ）依题意，记“甲投一次命中”为事件A，“乙投一次命中”为事件B，则

　　

　　甲、乙两人得分之和ξ的可能取值为0、1、2，则ξ概率分布为：

ξ	0	1	2
P

　　 Eξ=0×+1×+2×=

　　 答：每人在罚球线各投球一次，两人得分之和ξ的数学期望为.

　　（Ⅱ）∵事件“甲、乙两人在罚球线各投球二次均不命中”的概率为

　　

　　∴甲、乙两人在罚球线各投球两次至少有一次命中的概率

　　　

答：甲、乙两人在罚球线各投球二次，至少有一次命中的概率为

21解：

由的图象经过P（0，2），知d=2，所以

由在处的切线方程是，知

故所求的解析式是

22．（I）解法1：依题意，可设直线AB的方程为，

整理得　 ①

设①的两个不同的根，

　 ②

是线段AB的中点，得

解得k=-1，代入②得，>12，即的取值范围是（12，+）.

于是，直线AB的方程为

解法2：设

依题意，

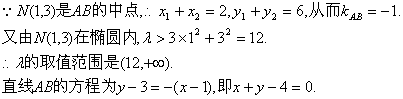
（II）解法1：代入椭圆方程，整理得

　③

③的两根，

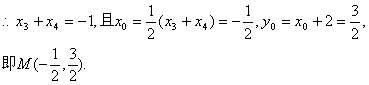
于是由弦长公式可得

　 ④

将直线AB的方程

　 ⑤

同理可得

　　⑥

假设在在>12，使得A、B、C、D四点共圆，则CD必为圆的直径，点M为圆心.点M到直线AB的距离为

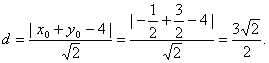　　 ⑦

于是，由④、⑥、⑦式和勾股定理可得

故当时，A、B、C、D四点均在以M为圆心，为半径的圆上.

（注：上述解法中最后一步可按如下解法获得：

A、B、C、D共圆△ACD为直角三角形，A为直角

　 ⑧

由⑥式知，⑧式左边=

由④和⑦知，⑧式右边=

　　　　　　　　　

∴⑧式成立，即A、B、C、D四点共圆

解法2：由（II）解法1及.

代入椭圆方程，整理得

　　　 ③

将直线AB的方程代入椭圆方程，整理得

　　　⑤

解③和⑤式可得　

不妨设

∴

计算可得，∴A在以CD为直径的圆上.

又B为A关于CD的对称点，∴A、B、C、D四点共圆.

（注：也可用勾股定理证明AC⊥AD）