高考全国试题分类解析（不等式）1

不等式

选择题：

1．（福建卷）不等式的解集是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （ A　 ）

　　　 A．　　　　　　　　　　　　B．

　　　 C．　　　　　　　　　　　　　　　　　　　　D．

2．（福建卷）下列结论正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　B  ）

　　　 A．当　　　　　 B．

　　　 C．的最小值为2　　　　　 D．当无最大值

3．（湖北卷）对任意实数a，b，c，给出下列命题：

　　　 ①“”是“”充要条件；　②“是无理数”是“a是无理数”的充要条件③“a>b”是“a²>b²”的充分条件；④“a<5”是“a<3”的必要条件.

　　　 其中真命题的个数是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（ B　 ）

　　　 A．1　　　　　　　　　　　　B．2　　　　　　　　　　　　C．3　　　　　　　　　　　　D．4

4. （辽宁卷）6．若，则的取值范围是　　　　　　　　　　　　　　　　　　　　　　 （ C　 ）

　　　 A．　　　　　　 B．　　　　　　　 C．　　　　　　　　 D．

5. （辽宁卷）在R上定义运算若不等式对任意实数成立，则　　　　　　　　　　　　　　　　　　　　　　　　　　 （ C　 ）

　　　 A．　　　　 B．　　　　　C．　　　D．

6. (全国卷Ⅰ) 设，函数，则使的的取值范围是（B）

（A）　　　 （B）　　　 （C）（D）

7. （山东卷），下列不等式一定成立的是（　A　）

（A）（B）

（C）

（D）

8. （天津卷）9．设是函数的反函数，则使成立的x的取值范围为（A ）　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　　 A． 　　B． 　　C． 　　　D．

9. （天津卷）已知＜＜ ，则

A．2^b＞2^a＞2^c　　　　　B．2^a＞2^b＞2^c 　　　　 C．2^c＞2^b＞2^a　　　 D．2^c＞2^a＞2^b

10. (重庆卷)不等式组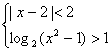的解集为　　　(C )　　　　　　　　　　　　　　　　　　　　　 　　(A) (0,)；　　　　　　(B) (,2)；　　　　　　 (C) (,4)；　　　　　　 (D) (2,4)。

11.(江西卷）已知实数a、b满足等式下列五个关系式：

　　　 ①0<b<a　②a<b<0　③0<a<b  ④b<a<0　⑤a=b

　　　 其中不可能成立的关系式有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （ B　 ）

　　　 A．1个　　　　　　　　　　B．2个　　　　　　　　　　C．3个　　　　　　　　　　D．4个

填空题：

7. (全国卷Ⅰ) （13）若正整数m满足，则m = 155　　　　 。

解答题：

1（湖北卷）22．（本小题满分14分）

　　　 已知不等式为大于2的整数，表示不超过的最大整数. 设数列的各项为正，且满足

　 （Ⅰ）证明

（Ⅱ）猜测数列是否有极限？如果有，写出极限的值（不必证明）；

（Ⅲ）试确定一个正整数N，使得当时，对任意b>0，都有

解：（Ⅰ）证法1：∵当

即　

于是有　

所有不等式两边相加可得　

由已知不等式知，当n≥3时有，

∵

证法2：设，首先利用数学归纳法证不等式

　 （i）当n=3时，　由

知不等式成立.

（ii）假设当n=k（k≥3）时，不等式成立，即

则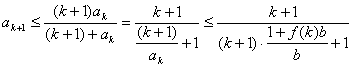

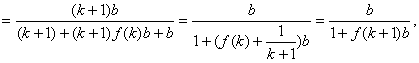
即当n=k+1时，不等式也成立.

由（i）、（ii）知，

又由已知不等式得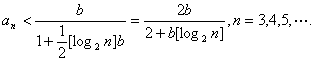　

　 （Ⅱ）有极限，且

　 （Ⅲ）∵

则有

故取N=1024，可使当n>N时，都有