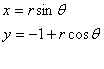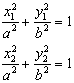2006年高考模拟测试数学1
第Ⅰ卷（选择题 共60分）
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。
1．已知集合
且
，若
则
（ ）
A．
B．
C．
D．
2．函数
的反函数的图象是 （ ）
 |
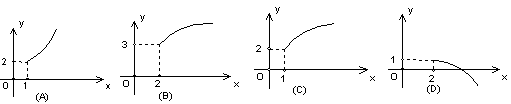3．若
，则
成立的一个充分不必要的条件是 （ ）
A.
B.
C.
D.
4．实数
满足
,则
的值为 （ ）
A．8 B．－8 C．8或－8 D．与θ有关
5．如图，正三棱锥A—BCD中，点E在棱AB上，点F在棱CD上，并使
，其中
，设α为异面直线EF与AC所成的角，β为异面直线EF与BD所成的角，则α+β的值为 （ ）
A．
B．
C．
D．与
有关的变量
6．已知点F1，F2分别双曲线
的左，右焦点，过F1且垂直于x轴的直线与双曲交于A，B两点，若△ABF2是锐角三角形，则该双曲线的离心率e的范围是（
）
A．（1，+∞） B．（1，1+
） C．（1，
） D．（1－
）
7．函数
与
有相同的定义域，且对定义域中任何x，有
，若g(x)=1的解集是{xx=0}，则函数F（x）=
是 （ ）
A．奇函数 B．偶函数
C．既是奇函数又是偶函数 D．非奇非偶函数
8．在轴截面是直角三角形的圆锥内，有一个体积最大的内接圆柱，则内接圆柱的体积与圆锥的体积的比值是 （ ）
A．
B．
C．
D．
9．当n∈N且n≥2时，1+2+22+…+24n-1=5p+q，其中p,q为非负整数，且0≤q＜5，则q的值为 （ ）
A.0 B.2 C.2 D.与n有关
10．过曲线C：x2+ay2=a外一点M作直线l1交曲线C于不同两点P1，P2，线段P1P2的中点为P，直线l2过P点和坐标原点O，若l1⊥l2，则a的值为 （ ）
A．1 B．2 C．－1 D．无法确定
11．在△ABC中，如果4sinA+2cosB=1,2sinB+4cosA=3,则∠C的大小是 （ ）
A．30° B．150° C．30°或150° D．60°或120°
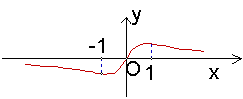12．若函数
的图象如图，则a的取值范围是
（ ）
A．（－∞,－1） B．（－1，0）
C．（0，1） D．（1，+∞）
第Ⅱ卷 (非选择题)
二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上。
13．某校编写了甲、乙、丙、丁四门选修课教材，在同一学年的五个班级试用。要求：每个班级只开设一门选修课；只有一、二班开设相同的选修课，且三班不开设甲门选修课，则不同的开设方法共有 种（用数字作答）
14．（理）函数
的最大值是
（文）函数
的最大值是
15．设正数数列{ an}为等比数列，且a2=4,a4=16,则
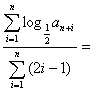
16．（理）给出下列命题：
①当x∈（-1，1）时arctgx>arcctgx;
②极坐标方程ρcscθ=1表示一条直线；
|
)〕=；
④方程
(r为参数，
)表示过点（0，-1）倾斜角为
的直线。
其中正确命题的序号有 （把你认为正确的都填上）
（文）给出下列命题：
①若α，β是第一象限角，且α＞β，则sinα＞sinβ;
②函数y=cos(2x+
)的图象的一条对称轴方程是x=－；
③把函数
的图象向左平移
个单位，得到函数
的图象；
④图象与函数
的图象关于直线
对称的函数是y=-tgx其中正确
命题的序号有
（把你认为正确的都填上）
三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤。
17．（本小题满分12分）
若方程
（其中
的两实根为α、β，数列1，
，（
，……的所有项的和为2－，试求θ的值。
18．（本小题满分12分）
已知z1是非零复数，argz1=
，且（1+
（其中k∈R）
（Ⅰ）试求复数z1;
（Ⅱ）(理)若z2≤1，试求arg（
）的取值范围；
（文）若z2=1,试求z1+z2+1的取值范围。
19．（本小题满分12分）
在直角梯形ABCD中，∠A=∠D=90°，AB＜CD，SD⊥平面ABCD，AB=AD=a，
S D=
，在线段SA上取一点E（不含端点）使EC=AC，截面CDE与SB交于点F。
（Ⅰ）求证：四边形EFCD为直角梯形；
（Ⅱ）求二面角B-EF-C的平面角的正切值；
（Ⅲ）设SB的中点为M，当
的值是多少时，能使△DMC为直角三角形？请给出证明。
20．（本小题满分12分）
一个有140名职工的合资企业投资生产甲、乙两种不同产品，2000年该企业生产的甲产品创外汇32万元，乙产品创外汇216万元，该企业以后每年所创外汇是甲产品以2.25倍的速度递增，而生产乙产品的机器由于老化的原因，每年创外汇为上年的
。这个企业只要年人均创外汇达3万元就可以列入国家重点企业。若以2000为第一年，问：
（Ⅰ）从哪一年开始，甲产品年创外汇超过乙产品年创外汇（lg2=0.3010,lg3=0.4771）
（Ⅱ）该企业哪一年所创外汇最少？该年甲、乙两种产品各创外汇多少万元？
（Ⅲ）该企业到2003年能否进入国家重点企业？
21．（本小题满分12分）
已知函数f(x)=ax2+4x+b,(a,b∈R，a<0),设关于x的方程f(x)=0的两实根为x1和x2,f(x)=x的两实根为α和β。
（Ⅰ）若a,b均为负整数，α-β=1,求f(x)的解析式；
（Ⅱ）（理）若α<1<β<2，求证：x1x2<2。
（文）若α为负整数，f(1)=0,求证：1≤x1-x2＜2.
22．（本小题满分14分）
已知A、B是椭圆
的一条弦，M（2，1）是AB中点，以M为焦点，以椭圆的右准线为相应准线的双曲线与直线AB交于N（4，-1）。
（Ⅰ）设双曲线的离率心为e，试将e表示为椭圆的半长轴长的函数。
（Ⅱ）当椭圆的离心率是双曲线的离心率的倒数时，求椭圆的方程。
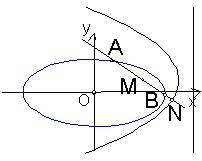（Ⅲ）求出椭圆的长轴长的取范围。
高考模拟测试1
数学参考答案
一、选择题
1．D 2．C 3．C 4．A 5．C 6．B 7．B 8．B 9．A 10．D 11．A 12．D
二、填空题
13．18； 14．理1，文1； 15．
；16．理③④，文②④
三、解答题
17．解：
、
是方程
的两实根
（1）
……4分
由已知
而
……8分
满足（2） 
不满足（1）故
……12分
18．解：
（Ⅰ）
则
……3分
即
解得 k=2,r=1 ……6分
理（Ⅱ）令
……9分
即
，于是
对应的点的轨迹为以（―1，―1）为圆心，以1为
半径的圆 
……12分
文（Ⅱ）
……8分
则
……10分
……12分
19．解：
（Ⅰ）∵ CD∥AB，AB
平面SAB ∴CD∥平面SAB面EFCD∩面SAB=EF，
∴CD∥EF ∵
又
面
∴
平面SAD，∴
又
为直角梯形 ……4分
（Ⅱ）
平面
∥
平面SAD 
即为二面角
D—EF—C的平面角 ……6分
中
而
且
为等腰三角形，
……8分
（Ⅲ）当
时，
为直角三角形
平面
平面
在
中，
为SB中点，
平面
平面 
为直角三角形 ……12分
20．解：
（Ⅰ）设第n年甲产品创外汇an万元，乙产品创外汇bn万元
则
若 
则
即
第3年开始即2002年甲产品创外汇就可以超过乙产品创外汇 ……4分
（Ⅱ）设该企业第n年创外汇
万元
则
当且仅当
即n=2时，取“=”号，即第2年，2001年创外汇最少为216万元，这年甲产品创外汇72万元，乙产品创外汇144万元 ……8分
（Ⅲ）2003年即第4年，设该企业创外汇为y
则
∴2003年该企业能进入国家重点企业。 ……12分
21．
（Ⅰ）
的两实根为
（1）
又令
则
的两实根为
（2）
……2分
……4分
即
均为负整数，
为负奇数，从而
满足（1），（2），故
……6分
|
|
|
……8分
且
即
……10分
由①得
……12分
（Ⅱ）（文）
又由（Ⅰ）得
即 
又
…… ……8分
不妨令
……10分
〔－1，0〕，
……12分
22．解
|
 |
∴
两式相减，得
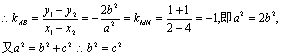……3分
|
则由双曲线定义及题设知 
（Ⅱ）
∴
，
而此时点M（2，1）在椭圆外，不可能是椭圆弦AB的中点，舍去。
故所求椭圆方程为
……10分
|
（Ⅲ）由题设知
联立
得
由（2）知
当
当
故
……14分