高考第一轮复习数学：排列、组合和二项式定理（附答案）

素质能力检测（4）

一、填空题（每小题5分，共30分）

1.（2004年东北三校模拟题）已知下图的每个开关都有闭合与不闭合两种可能，因此5个开关共有2⁵种可能.在这2⁵种可能中，电路从P到Q接通的情况有

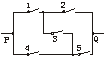
A.30种  　　　　　　　　　　 B.10种  　　　　　　　　　　 C.24种  　　　　　　　　　　 D.16种

解析：五个开关全闭合有1种情况能使电路接通；四个开关闭合有5种情况能使电路接通；三个开关闭合有8种情况能使电路接通；两个开关闭合有2种情况能使电路接通.所以共有1+5+8+2=16种情况能使电路接通.

答案：D

2.（2004年湖北八校模拟题）有七名同学站成一排照毕业纪念照，其中甲必须站在正中间，并且乙、丙两位同学要站在一起，则不同的站法有

A.240种　　　　　　　　　　　B.192种　　　　　　　　　　　 C.96种　　　　　　　　　　　　D.48种

解析：我们可以这样排，首先将乙、丙绑定为一个位置，排法有AA种，然后将甲站在中间位置，但此时有不符合条件的，即当乙、丙在中间位置时，甲再插入中间，应去掉，共有A·A种，则符合条件的站法有A·A－A·A=192种，选B.

答案：B

3.（理）在（1+x）³+（1+x）⁴+…+（1+x）²⁰⁰⁴的展开式中x³的系数等于

A.C　　　　　　　　　　　　B.C　　　　　　　　　　　　C.2C　　　　　　　　　　　D.2C

解析：含x³的系数为C+C+C+…+C=C.故选B.

答案：B

（文）在（－）⁵的展开式中的系数等于

A.10　　　　　　　　　　　　　　　　　 B.－10　　　　　　　　　　　　 C.20　　　　　　　　　　　　　　　　　 D.－20

解析：本题考查二项式定理，（a+b）ⁿ中第r+1项T=C·a^r·b^n－r，

则T=C（）^r·（）^5－r=C·2^－r·（－2）^5－r·x^2r－5.

由题知2r－5=－1，则r=2，则的系数为C·2^－2·（－2）^5－2=C××（－8）=－20，故选D.

答案：D

4.如下图，A、B、C、D为海上的四个小岛，要建三座桥，将这四个小岛连接起来，则不同的建桥方案共有

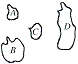
A.8种　　　　　　　　　　　　　B.12种　　　　　　　　　　　　C.16种　　　　　　　　　　　　D.20种

解法一：桥梁的建设有两大类：

（1）A、B、C、D四岛之间依次建桥，如AB、BC、CD一种方案，AC、CD、DB一种方案等.其建造方案共有m₁==12（种）.

（2）四岛中的某一岛与其他三岛之间建桥，如AB、AC、AD等其建造方案共有m₂=C=4（种）.

由分类计数原理可知N=m₁+m₂=16（种）.

解法二：把四个岛看成三棱锥的四个顶点，四棱锥有6条棱，从中选3条把A、B、C、D连起来，有C种方法，其中共面时不合题意，则共有C－4=16（种）.

答案：C

5.登山运动员10人，平均分为两组，其中熟悉道路的4人，每组都需要2人，那么不同的分配方法种数是

A.30　　　　　　　　　　　　　　　　　 B.60　　　　　　　　　　　　　　 C.120　　　　　　　　　　　　　 D.240

解析：先将4个熟悉道路的人平均分成两组有.

再将余下的6人中分成两组有C·C.

故有C·C=60（种）.

答案：B

6.（2004年北京东城区模拟题）某银行储蓄卡的密码是一个4位数码，某人采用千位、百位上的数字之积作为十位、个位上的数字（如2816）的方法设计密码，当积为一位数时，十位上数字选0，千位、百位上都能取0.这样设计出来的密码共有

A.90个　　　　　　　　　　　　B.99个　　　　　　　　　　　　C.100个　　　　　　　　　　　D.112个

解析：由于千位、百位确定下来后十位、个位就随之确定，则只考虑千位、百位即可，千位、百位各有10种选择，

所以有10×10种=100种.故选C.

答案：C

二、填空题（每小题4分，共16分）

7.从1，3，5中任取2个数字，从0，2，4，6中任取2个数字，组成没有重复数字的四位数，其中能被5整除的四位数共有_____________个.（用数字作答）

解析：能被5整除的四位数的个位数只能是5或0，

∴必须从1，3，5中选取5或从0，2，4，6中选取0.

（1）选取0不选取5，能被5整除的四位数有C·C·A=36（个）；

（2）选取5不选取0，能被5整除的四位数有CC·A=36（个）.

（3）同时选取0和5，能被5整除的四位数有CC（A+AA）=60（个）.

∴其中能被5整除的四位数共有132个.

答案：132

8.有A、B、C、D、E五位学生参加网页设计比赛，决出了第一到第五的名次.A、B两位学生去问成绩，教师对A说：你的名次不知道，但肯定没得第一名；又对B说：你是第三名.请你分析一下，这五位学生的名次排列共有_____________种不同的可能.（用数字作答）

解法一：A不是第一名有A种.A不是第一名，B不是第三名有A种.符合要求的有A－A=18种.

解法二：第一名有3种，第二名有3种，第三名有1种，第四名有2种，第五名有1种，则完成这件事有3×3×1×2×1=18种.

答案：18

9.若（1－2x）²⁰⁰⁴=a₀+a₁x+a₂x²+…+a₂₀₀₄x²⁰⁰⁴（x∈R），则（a₀+a₁）+（a₀+a₂）+（a₀+a₃）+…+（a₀+a₂₀₀₄）=_____________.（用数字作答）

解析：在（1－2x）²⁰⁰⁴=a₀+a₁x+a₂x²+…+a₂₀₀₄x²⁰⁰⁴中令x=1，

得a₀+a₁+a₂+…+a₂₀₀₄=（1－2）²⁰⁰⁴=1，

又a₀=1，∴a₁+a₂+…+a₂₀₀₄=0.

∴（a₀+a₁）+（a₀+a₂）+（a₀+a₃）+…+（a₀+a₂₀₀₄）=2004.

答案：2004

10.将标号为1，2，…，10的10个球放入标号为1，2，…，10的10个盒子内，每个盒子内放一个球，恰好有2个球的标号与其所在盒子的标号不一致的放入方法种数为_____________.（用数字作答）

解析：分两步：第一步，先取8个球，分别放入球的标号与盒子的标号相同的盒子里有C种放法.

第二步，再将余下的2个球放入盒子里的放法有1种.

由分步计数原理得C=45.

答案：45

三、解答题（本大题共4小题，共54分）

11.（12分）中央电视台“正大综艺”节目的现场观众来自四个单位，分别在图中4个区域内坐定.有4种不同颜色的服装，每个单位的观众必须穿同种颜色的服装，且相邻两个区域的颜色不同，不相邻区域颜色相同与否则不受限制，那么不同的着装方法有多少种?

分析：显然，相对位置（比如Ⅰ，Ⅲ）的服装颜色可以相同，也可以不同，因为它们不相邻，但它们服装颜色是否相同对另两个区域（Ⅱ，Ⅳ）的服装颜色的影响是不同的，所以考虑以此为分类讨论的标准.

解法一：若每个区域服装颜色不相同，则有C·C·C·1=24种；若Ⅰ、Ⅲ或Ⅱ、Ⅳ同色，另两区域不同色，则有2C×3×2=48种；若Ⅰ、Ⅲ与Ⅱ、Ⅳ分别同色，则有C· A=12种.故共有24+48+12=84种.

解法二：Ⅰ有4种可能，Ⅱ有3种可能，Ⅲ可与Ⅰ相同或不同，故共有4×3×3+4×3×2×2=84种方法.

12.（14分）（理）某人手中有5张扑克牌，其中2张为不同花色的2，3张为不同花色的A，有5次出牌机会，每次只能出一种点数的牌但张数不限，此人有多少种不同的出牌方法?

解：由于张数不限，2张2，3张A可以一起出，亦可分几次出，可以考虑按此分类.

出牌的方法可分为以下几类：

（1）5张牌全部分开出，有A种方法；

（2）2张2一起出，3张A一起出，有A种方法；

（3）2张2一起出，3张A分开出，有A种方法；

（4）2张2一起出，3张A两次出，有CA种方法；

（5）2张2分开出，3张A一起出，有A种方法；

（6）2张2分开出，3张A分两次出，有CA种方法.

因此，共有不同的出牌方法A+A+A+CA+ A+CA=860种.

（文）抛物线方程y=ax²+bx+c的各项系数a、b、c∈{－2，－1，0，1，2，3，4}，且a、b、c两两不等.

（1）过原点的抛物线有多少条?

（2）过原点且顶点在第一象限的抛物线有多少条?

解：（1）抛物线过原点，则c=0.从－2，－1，1，2，3，4中任取2个数作为a、b，有A=30条.

（2）∵顶点在第一象限，

∴

∴C·C·C=9.

∴过原点且顶点在第一象限的抛物线有9条.

13.（14分）7名学生站成一排，下列情况各有多少种不同排法?

（1）甲、乙必须排在一起；

（2）甲不在排头，乙不在排尾；

（3）甲、乙、丙互不相邻；

（4）甲、乙之间必须隔一人.

解：（1）（整体排列法）先将甲、乙看作一个人，有A种排法，然后甲、乙换位，所以不同的排法有A·A=1440种.

（2）（间接法）甲在排头或乙在排尾的排法共2A种，其中都包含甲在排头且乙在排尾的情形，故有不同的排法A－2A+A=3720种.

（3）（插空法）把甲、乙、丙插入其余4个元素产生的5个空，有A·A=1440种.

（4）先从其余5人中选1人有5种选法，放在甲、乙之间，将三人看作一个有A种，然后甲、乙换位有A种，共有5AA=1200种方法.

评述：解决“相邻”问题一般用整体法，解决不相邻问题一般用插空法，解决某些元素在某些位置用定位法，解决某些元素不在某些位置一般用间接法.

14.（14分）已知（1+3x）ⁿ的展开式中，末三项的二项式系数的和等于121，求展开式中系数最大的项及二项式系数最大的项.

解：末三项的二项式系数分别为C、C、C，

由题设，得C+C+C=121，

即C+C+1=121，∴n²+n－240=0.

∴n=15（n=－16舍去）.

∵T=C（3x）^r=C·3^rx^r，

设T项与T_r项的系数分别为t与t_r，

则t=C3^r，t_r=C·3，令>1，

即= >1，

解得r<12.

也就是说，当r取小于12的自然数时，都有t_r<t，即第12项以前的各项，前面一项的系数都比后面一项的系数小.

又当r=12时，t=t_r，即t₁₃=t₁₂，

∴展开式中系数最大的项是T₁₂=C·3¹¹·x¹¹，T₁₃=C·3¹²·x¹²，

当n=15时，二项式系数最大的是第8、9项，

分别为C·3⁷·x⁷与C·3⁸·x⁸.

评述：本题考查二项式系数的性质、二项式定理、二项式系数与项的系数以及运算能力.注意二项展开式中，项的系数与项的二项式系数是两个不同的概念，前者由指数、底数二者决定，而后者只与二项式次数有关，一般地，项的系数不具备二项式系数的性质，不能混用.在（a+b）ⁿ的展开式中，系数最大的项是中间项；但当a、b的系数不是1时，最大系数值的项的位置就不一定在中间，需要利用通项公式，根据系数值的增减性具体讨论而定.