新教材高考数学模拟题精编详解第九套试题
| 题号 | 一 | 二 | 三 | 总分 | ||||||||
| 1~12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | ||
| 分数 | ||||||||||||
说明:本套试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分.考试时间:120分钟.
第Ⅰ卷(选择题,共60分)
一、本题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一个选项是符合题目要求的.
1.两个非零向量e![]() ,e
,e![]() 不共线,若(ke
不共线,若(ke![]() +e
+e![]() )∥(e
)∥(e![]() +ke
+ke![]() ),则实数k的值为( )
),则实数k的值为( )
A.1 B.-1 C.±1 D.0
2.有以下四个命题,其中真命题为( )
A.原点与点(2,3)在直线2x+y-3=0的同侧
B.点(2,3)与点(3,1)在直线x-y=0的同侧
C.原点与点(2,1)在直线2y-6x+1=0的异侧
D.原点与点(2,1)在直线2y-6x+1=0的同侧
3.①某高校为了解学生家庭经济收入情况,从来自城镇的150名学生和来自农村的150名学生中抽取100名学生的样本;②某车间主任从100件产品中抽取10件样本进行产品质量检验.
I.随机抽样法;Ⅱ.分层抽样法.
上述两问题和两方法配对正确的是( )
A.①配I,②配Ⅱ B.①配Ⅱ,②配Ⅰ
C.①配I,②配I D.①配Ⅱ,②配Ⅱ
4.已知函数![]() ,其反函数为
,其反函数为![]() ,则
,则![]() 是( )
是( )
A.奇函数且在(0,+∞)上单调递减
B.偶函数且在(0,+∞)上单调递增
C.奇函数且在(-∞,0)上单调递减
D.偶函数且在(-∞,0)上单调递增
5.以下四个命题:
①过一点有且仅有一个平面与已知直线垂直;
②若平面外两点到平面的距离相等,则过这两点的直线必平行于该平面;
③两条相交直线在同一平面内的射影必为相交直线;
④两个互相垂直的平面,一个平面内的任一直线必垂直于另一平面的无数条直线.
其中正确的命题是( )
A.①和② B.②和③ C.③和④ D.①和④
6.从单词“education”中选取5个不同的字母排成一排,则含“at”(“at”相连且顺序不变)的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知正二十面体的各面都是正三角形,那么它的顶点数为( )
A.30 B.12 C.32 D.10
8.已知![]() 的展开式中,
的展开式中,![]() 系数为56,则实数a的值为( )
系数为56,则实数a的值为( )
A.6或5 B.-1或4
C.6或-1 D.4或5
9.对某种产品市场产销量情况如图所示,其中:![]() 表示产品各年年产量的变化规律;
表示产品各年年产量的变化规律;![]() 表示产品各年的销售情况.下列叙述:
表示产品各年的销售情况.下列叙述:
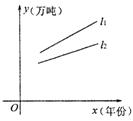
(1)产品产量、销售量均以直线上升,仍可按原生产计划进行下去;
(2)产品已经出现了供大于求的情况,价格将趋跌;
(3)产品的库存积压将越来越严重,应压缩产量或扩大销售量;
(4)产品的产、销情况均以一定的年增长率递增.你认为较合理的是( )
A.(1),(2),(3) B.(1),(3),(4)
C.(2),(4) D.(2),(3)
10.(文)函数![]() 的最小正周期是( )
的最小正周期是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(理)函数![]() 是( )
是( )
A.周期为![]() 的偶函数 B.周期为
的偶函数 B.周期为![]() 的奇函数
的奇函数
C.周期为2![]() 的偶函数 D.周期为2
的偶函数 D.周期为2![]() 的奇函数
的奇函数
11.(文)如图,正四面体ABCD中,E为AB中点,F为CD的中点,则异面直线EF与SA所成的角为( )
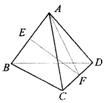
A.90° B.60° C.45° D.30°
(理)如图,正三棱柱![]() 中,AB=
中,AB=![]() ,则
,则![]() 与平面
与平面![]() 所成的角的正弦值为( )
所成的角的正弦值为( )
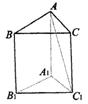
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.(文)抛物线![]() 的焦点在x轴上,则实数m的值为( )
的焦点在x轴上,则实数m的值为( )
A.0 B.![]() C.2 D.3
C.2 D.3
(理)已知椭圆![]() (a>0)与A(2,1),B(4,3)为端点的线段没有公共点,则a的取值范围是( )
(a>0)与A(2,1),B(4,3)为端点的线段没有公共点,则a的取值范围是( )
A.![]() B.
B.![]() 或
或![]()
C.![]() 或
或![]() D.
D.![]()
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 得分 |
| 答案 |
第Ⅱ卷(非选择题,共90分)
二、填空题:本题共4小题,共16分,把答案填在题中的横线上
13.已知a=(3,4),a-b=1,则b的范围是________.
14.已知直线y=x+1与椭圆![]() (m>n>0)相交于A,B两点,若弦AB的中点的横坐标等于
(m>n>0)相交于A,B两点,若弦AB的中点的横坐标等于![]() ,则双曲线
,则双曲线![]() 的两条渐近线的夹角的正切值等于________.
的两条渐近线的夹角的正切值等于________.
15.某县农民均收入服从![]() =500元,
=500元,![]() =20元的正态分布,则此县农民年均收入在500元到520元间人数的百分比为________.
=20元的正态分布,则此县农民年均收入在500元到520元间人数的百分比为________.
16.![]() =________.
=________.
三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤.
17.(12分)已知a=(![]() ,
,![]() ),b=(
),b=(![]() ,
,![]() ),a与b之间有关系式ka+b=
),a与b之间有关系式ka+b=![]() a-kb,其中k>0.
a-kb,其中k>0.
(1)用k表示a、b;
(2)求a·b的最小值,并求此时,a与b的夹角![]() 的大小.
的大小.
18.(12分)已知a、b、m、![]() ,
,![]() 是首项为a,公差为b的等差数列;
是首项为a,公差为b的等差数列;![]() 是首项为b,公比为a的等比数列,且满足
是首项为b,公比为a的等比数列,且满足![]() .
.
(1)求a的值;
(2)数列![]() 与数列
与数列![]() 的公共项,且公共项按原顺序排列后构成一个新数列
的公共项,且公共项按原顺序排列后构成一个新数列![]() ,求
,求![]() 的前n项之和
的前n项之和![]() .
.
19.已知:![]() (a>1>b>0).
(a>1>b>0).
(1)求![]() 的定义域;
的定义域;
(2)判断![]() 在其定义域内的单调性;
在其定义域内的单调性;
(3)若![]() 在(1,+∞)内恒为正,试比较a-b与1的大小.
在(1,+∞)内恒为正,试比较a-b与1的大小.
20.如图,某建筑物的基本单元可近似地按以下方法构作:先在地平面![]() 内作菱形ABCD,边长为1,∠BAD=60°,再在
内作菱形ABCD,边长为1,∠BAD=60°,再在![]() 的上侧,分别以△
的上侧,分别以△![]() 与△
与△![]() 为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
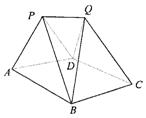
(1)求证:PQ⊥BD;
(2)求二面角P-BD-Q的余弦值;
(3)求点P到平面QBD的距离;
21.(12分)在Rt△ABC中,∠CAB=90°,AB=2,AC=![]() ,一曲线E过C点,动点P在曲线E上运动,且保持
,一曲线E过C点,动点P在曲线E上运动,且保持![]() 的值不变.
的值不变.
(1)建立适当的坐标系,求曲线E的方程;
(2)直线l:![]() 与曲线E交于M,N两点,求四边形MANB的面积的最大值.
与曲线E交于M,N两点,求四边形MANB的面积的最大值.
22.(14分)(理)已知函数![]() ,记函数
,记函数![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…,考察区间A=(-∞,0),对任意实数
,…,考察区间A=(-∞,0),对任意实数![]() ,有
,有![]() ,
,![]() ,且n≥2时,
,且n≥2时,![]() ,问:是否还有其它区间,对于该区间的任意实数x,只要n≥2,都有
,问:是否还有其它区间,对于该区间的任意实数x,只要n≥2,都有![]() ?
?
(文)已知二次函数![]() 的二次项系数为负,对任意实数x都有
的二次项系数为负,对任意实数x都有![]() ,问当
,问当![]() 与
与![]() 满足什么条件时才有-2<x<0?
满足什么条件时才有-2<x<0?
参考答案
1.C 2.C 3.B 4.D 5.D 6.A 7.B 8.C 9.D
10.(文)B (理)B 11.(文)C (理)C 12.(文)B (理)B 13.[4,6]
14.![]() 15.34.15% 16.
15.34.15% 16.![]()
17.解析:由已知![]() .
.
∵ ![]() ,
,
∴ ![]() .
.
∴ ![]() . ∵ k>0, ∴
. ∵ k>0, ∴ ![]() .
.
此时![]() ∴
∴ 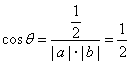 . ∴
. ∴ ![]() =60°.
=60°.
18.解析:(1)∵ ![]() ,
,![]() ,
,
由已知a<b<a+b<ab<a+2b,
∴ 由a+2b<ab,a、![]() 得
得![]() .
.
∵ ![]() , ∴ a≥2.
, ∴ a≥2.
又得![]() ,而
,而![]() , ∴ b≥3.
, ∴ b≥3.
再由ab<a+2b,b≥3,得![]() .
.
∴ 2≤a<3 ∴ a=2.
(2)设![]() ,即
,即![]() .
.
∴ ![]() ,
,![]() .
.
∵ b≥3, ∴ ![]() . ∴
. ∴ ![]() .
.
∴ ![]() .
.
故![]() .
.
19.解析:(1)由![]() , ∴
, ∴ ![]() ,
,![]() . ∴ x>0.
. ∴ x>0.
∴ 定义域为(0,+∞).
(2)设![]() , a>1>b>0
, a>1>b>0
∴ ![]()
![]()
![]()
∴ ![]() ∴
∴ ![]() .
.
∴ ![]() . ∴
. ∴ ![]() 在(0,+∞)是增函数.
在(0,+∞)是增函数.
(3)当![]() ,+∞
,+∞![]() 时,
时,![]() ,要使
,要使![]() ,须
,须![]() , ∴ a-b≥1.
, ∴ a-b≥1.
20.解析:(1)由P-ABD,Q-CBD是相同正三棱锥,可知△PBD与△QBD是全等等腰△.取BD中点E,连结PE、QE,则BD⊥PE,BD⊥QE.故BD⊥平面PQE,从而BD⊥PQ.
(2)由(1)知∠PEQ是二面角P-BD-Q的平面角,作PM⊥平面![]() ,垂足为M,作QN⊥平面
,垂足为M,作QN⊥平面![]() ,垂足为N,则PM∥QN,M、N分别是正△ABD与正△BCD的中心,从而点A、M、E、N、C共线,PM与QN确定平面PACQ,且PMNQ为矩形.可得ME=NE=
,垂足为N,则PM∥QN,M、N分别是正△ABD与正△BCD的中心,从而点A、M、E、N、C共线,PM与QN确定平面PACQ,且PMNQ为矩形.可得ME=NE=![]() ,PE=QE=
,PE=QE=![]() ,PQ=MN=
,PQ=MN=![]() ,∴ cos∠PEQ=
,∴ cos∠PEQ=![]() ,即二面角平面角为
,即二面角平面角为![]() .
.
(3)由(1)知BD⊥平面PEQ.设点P到平面QBD的距离为h,则
![]()
∴ ![]() .
.
∴ ![]() . ∴
. ∴ ![]() .
.
21.解析:(1)以AB为x轴,以AB中点为原点O建立直角坐标系.
∵ ![]() ,
,
∴ 动点轨迹为椭圆,且![]() ,c=1,从而b=1.
,c=1,从而b=1.
∴ 方程为 ![]() .
.
(2)将y=x+t代入![]() ,得
,得![]() .
.
设M(![]() ,
,![]() )、N(
)、N(![]() ,
,![]() ),
),
∴ 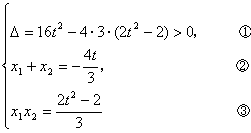
由①得![]() <3.
<3.
∴ ![]() .
.
∴ t=0时,![]() .
.
22.解析:(理)![]() ,即
,即![]() ,故x<0或x>1.
,故x<0或x>1.
∴ ![]() 或
或![]() .
.
要使一切![]() ,n≥2,都有
,n≥2,都有![]() ,必须使
,必须使![]() 或
或![]() ,
,
∴ ![]() 或
或![]() ,即
,即![]() 或
或![]() .
.
解得x<0或x>1或![]()
![]() .
.
∴ 还有区间(![]() ,
,![]() )和(1,+∞)使得对于这些区间内的任意实数x,只要n≥2,都有
)和(1,+∞)使得对于这些区间内的任意实数x,只要n≥2,都有![]() .
.
(文)由已知![]() ,
,![]() .
.
∴ ![]() 在(-∞,
在(-∞,![]() 上单增,在(2,+∞)上单调.
上单增,在(2,+∞)上单调.
又∵ ![]() ,
,![]() .
.
∴ 需讨论![]() 与
与![]() 的大小.
的大小.
由![]() 知
知
当![]() ,即
,即![]() 时,
时,![]() .
.
故![]() 时,应有
时,应有![]() .
.