素质能力检测(十五)
一、选择题(每小题5分,共30分)
1.如果复数![]() (其中i为虚数单位,b为实数)的实部和虚部互为相反数,那么b等于
(其中i为虚数单位,b为实数)的实部和虚部互为相反数,那么b等于
A.![]() B.
B.![]() C.-
C.-![]() D.2
D.2
解析:![]() =
=![]() =
=![]()
∴2-2b=b+4,b=-![]() .
.
答案:C
2.当![]() <m<1时,复数z=(3m-2)+(m-1)i在复平面上对应的点位于
<m<1时,复数z=(3m-2)+(m-1)i在复平面上对应的点位于
A.第一象限 B.第二象限
C.第三象限 D.第四象限
解析:z对应的点为(3m-2,m-1),
∵![]() <m<1,
<m<1,
∴0<3m-2<1,-![]() <m-1<0.
<m-1<0.
答案:D
3.在下列命题中,正确命题的个数为
①两个复数不能比较大小;
②z1、z2、z3∈C,若(z1-z2)2+(z2-z3)2=0,则z1=z3;
③若(x2-1)+(x2+3x+2)i是纯虚数,则实数x=±1;
④z为虚数的一个充要条件是z+![]() ∈R;
∈R;
⑤若a、b是两个相等的实数,则(a-b)+(a+b)i是纯虚数;
⑥复数z∈R的一个充要条件是z=![]() .
.
A.0 B.1 C.2 D.3
解析:①错,两个复数如果都是实数则可比较大小;②错,当z1、z2、z3不全是实数时不成立,如z1=i,z2=1+i,z3=1时满足条件,但z1≠z3;③错,当x=-1时,虚部也为零,原数是实数;④错,此条件是必要非充分条件;⑤错,当a=b=0时,原数是实数;⑥对.
答案:B
4.设f(n)=(![]() )n+(
)n+(![]() )n(n∈Z),则集合{x|x=f(n)}中元素的个数是
)n(n∈Z),则集合{x|x=f(n)}中元素的个数是
A.1 B.2 C.3 D.无穷多个
解析:∵f(n)=in+(-i)n,
∴f(0)=2,f(1)=i-i=0,f(2)=-1-1=-2,f(3)=-i+i=0.
∴{x|x=f(n)}={-2,0,2}.
答案:C
5.已知复平面内的圆M:z-2=1,若![]() 为纯虚数,则与复数p对应的点P
为纯虚数,则与复数p对应的点P
A.必在圆M上 B.必在圆M内
C.必在圆M外 D.不能确定
解析:∵![]() 为纯虚数,设为ki(k∈R,k≠0),
为纯虚数,设为ki(k∈R,k≠0),
∴(1-ki)p=1+ki,取模得p=1且p≠1.
∴选C.
答案:C
6.已知复数(x-2)+yi(x、y∈R)的模为![]() ,则
,则![]() 的最大值是
的最大值是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
解析:∵|x-2+yi|=![]() ,
,
∴(x-2)2+y2=3.
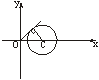
∴(x,y)在以C(2,0)为圆心、以![]() 为半径的圆上,如右图,由平面几何知识知
为半径的圆上,如右图,由平面几何知识知![]() .
.
答案:D
二、填空题(每小题4分,共16分)
7.已知M={1,2,(a2-3a-1)+(a2-5a-6)i},N={-1,3},M∩N={3},实数a=_________.
解析:按题意(a2-3a-1)+(a2-5a-6)i=3,
∴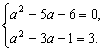 解得a=-1.
解得a=-1.
答案:-1
8.复数z=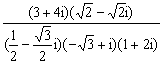 -2i的模为_______________.
-2i的模为_______________.
解析:由复数的模的性质可知
z=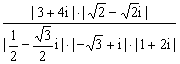 -2i
-2i
=![]() -2i=
-2i=![]() -2i,∴z=3.
-2i,∴z=3.
答案:3
9.若x、y∈R,且2x-1+i=y-(3-y)i,则x=__________,y=___________.
解析:根据复数相等的定义求得.
答案:![]() 4
4
10.复数z满足z·![]() +z+
+z+![]() =3,则z对应点的轨迹是____________.
=3,则z对应点的轨迹是____________.
解析:设z=x+yi(x、y∈R),则x2+y2+2x=3表示圆.
答案:以点(-1,0)为圆心,2为半径的圆
三、解答题(本大题共4小题,共54分)
11.(12分)设复数z1、z2满足z1·z2+2iz1-2iz2+1=0,![]() -z1=2i,求z1和z2.
-z1=2i,求z1和z2.
解:∵![]() -z1=2i,∴
-z1=2i,∴![]() =z1+2i.
=z1+2i.
∴z2=![]() ,即z2=
,即z2=![]() -2i.
-2i.
又∵z1·z2+2iz1-2iz2+1=0,
∴z1(![]() -2i)+2iz1-2i(
-2i)+2iz1-2i(![]() -2i)+1=0,
-2i)+1=0,
即![]() 2-2i
2-2i![]() -3=0.
-3=0.
令z1=a+bi(a、b∈R),
得a2+b2-2b-3-2ai=0,
即![]() 解得
解得![]()
∴z1=3i,z2=-5i或z1=-i,z2=-i.
12.(14分)设复数z满足4z+2![]() =3
=3![]() +i,ω=sinθ-icosθ(θ∈R),求z的值和z-ω的取值范围.
+i,ω=sinθ-icosθ(θ∈R),求z的值和z-ω的取值范围.
解:设z=a+bi(a、b∈R),则![]() =a-bi,代入4z+2
=a-bi,代入4z+2![]() =3
=3![]() +i,得
+i,得
4(a+bi)+2(a-bi)=3![]() +i,
+i,
即6a+2bi=3![]() +i.
+i.
∴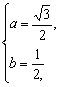 ∴z=
∴z=![]() i.
i.
z-ω=![]() +
+![]() i-(sinθ-icosθ)
i-(sinθ-icosθ)
=![]()
=![]() =
=![]() .
.
∵-1≤sin(θ-![]() )≤1,∴0≤2-2sin(θ-
)≤1,∴0≤2-2sin(θ-![]() )≤4.∴0≤z-ω≤2.
)≤4.∴0≤z-ω≤2.
13.(14分)非零复数a、b、c满足![]() =
=![]() =
=![]() ,求
,求![]() 的值.
的值.
解:设![]() =
=![]() =
=![]() =k,则a=bk,b=ck,c=ak,即c=ak,b=ak·k=ak2,a=ak2·k=ak3,
=k,则a=bk,b=ck,c=ak,即c=ak,b=ak·k=ak2,a=ak2·k=ak3,
∴k3=1.∴k=1或k=-![]() ±
±![]() i.
i.
则![]() =
=![]() =
=![]() .
.
若k=1,则原式=1;
若k=-![]() +
+![]() i,则原式=-
i,则原式=-![]() -
-![]() i;
i;
若k=-![]() -
-![]() i,则原式=-
i,则原式=-![]() +
+![]() i.
i.
综上,![]() 的值分别为1,-
的值分别为1,-![]() -
-![]() i,-1+
i,-1+![]() i.
i.
14.(14分)设复数z满足|z|=5,且(3+4i)z在复平面上对应的点在第二、四象限的角平分线上,|![]() z-m|=5
z-m|=5![]() (m∈R),求z和m的值.
(m∈R),求z和m的值.
解:设出z的代数形式z=x+yi(x、y∈R).
∵|z|=5,∴x2+y2=25.
∵(3+4i)z=(3+4i)(x+yi)
=(3x-4y)+(4x+3y)i,
又(3+4i)z在复平面内对应的点在第二、四象限的角平分线上,则它的实部与虚部互为相反数,∴3x-4y+4x+3y=0.
化简得y=7x.将其代入x2+y2=25,得x=±![]() ,y=±
,y=±![]() .
.
∴z=±(![]() +
+![]() i).则当z=
i).则当z=![]() +
+![]() i时,
i时,
|![]() z-m|=|1+7i-m|=5
z-m|=|1+7i-m|=5![]() ,
,
即(1-m)2+72=50.解得m=0或m=2.
当z=-(![]() +
+![]() i)时,同理可得m=0或m=-2.
i)时,同理可得m=0或m=-2.