2006年高考模拟测试数学6
第Ⅰ卷(选择题 共60分)
| |
(1)化简![]() 得 ( )
得 ( )
(A)![]() (B)
(B)![]() (C)1 (D)-1
(C)1 (D)-1
(2)双曲线![]() 的一个焦点是(0,-3),则k的值是 ( )
的一个焦点是(0,-3),则k的值是 ( )
(A)1 (B)-1 (C)![]() (D)-
(D)-![]()
(3)已知![]() 过点(3,5),g(x)与f(x)关于直线x=2对称,则y=g(x)必过
过点(3,5),g(x)与f(x)关于直线x=2对称,则y=g(x)必过
点 ( )
(A)(-1,3) (B)(5,3) (C)(-1,1) (D)(1,5)
(4)已知复数![]() ,则
,则![]() ( )
( )
(A)![]() (B)-
(B)-![]() (C)
(C)![]() (D)
(D)![]()
(5)(理)曲线![]() 上有且仅有三点到直线
上有且仅有三点到直线![]() 的距离为1,则r属于集合 ( )
的距离为1,则r属于集合 ( )
(A)![]() (B)
(B)![]()
(C)![]() (D){9}
(D){9}
(文)已知两条直线![]() ,其中a为实数,当这两条直线的夹角
,其中a为实数,当这两条直线的夹角
在![]() 内变动时,a的取值范围是 ( )
内变动时,a的取值范围是 ( )
(A)(0,1) (B)![]() (C)
(C)![]() (D)
(D)![]()
6.半径为2cm的半圆纸片卷成圆锥放在桌面上,一阵风吹倒它,它的最高处距桌面( )
(A)4cm (B)2cm (C)![]() (D)
(D)![]()
7.(理)![]() 的值等于 ( )
的值等于 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(文)函数![]() 的最小正周期为 ( )
的最小正周期为 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)2
(D)2![]()
8.某校有6间电脑室,每晚至少开放2间,则不同安排方案的种数为 ( )
①![]() ②
②![]() ③
③![]() ④
④![]()
其中正确的结论为 ( )
(A)仅有① (B)有②和③ (C)仅有② (D)仅有③
9.正四棱锥P—ABCD的底面积为3,体积为![]() E为侧棱PC的中点,则PA与BE所成
E为侧棱PC的中点,则PA与BE所成
的角为 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
10.给出四个函数,分别满足①![]() ②
②![]()
③![]() ④
④![]() 又给出四个函数的图象
又给出四个函数的图象
 |
则正确的配匹方案是 ( )
(A)①—M ②—N ③—P ④—Q (B)①—N ②—P ③—M ④—Q
(C)①—P ②—M ③—N ④—Q (D)①—Q ②—M ③—N ④—P
11.P是双曲线![]() 左支上一点,F1、F2分别是左、右焦点,且焦距
左支上一点,F1、F2分别是左、右焦点,且焦距
为2c,则![]() 的内切圆的圆心横坐标为 ( )
的内切圆的圆心横坐标为 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
12.某债券市场发行的三种值券:甲种面值为100元,一年到期本利共获103元;乙种面
值为50元,半年期本利共50.9元;丙种面值为100元,但买入时只付97元,一年到
期拿回100元,这三种投资收益比例从小到大排列为 ( )
(A)乙,甲,丙 (B)甲、丙、乙 (C)甲、乙、丙 (D)丙、甲、乙
第Ⅱ卷 (非选择题)
| |
13.一个球的内接长方体的长、宽、高分别为1,2,3,则这个球的表面积是 .
14.若![]() 展开式中的x3项的系数为20,则非零实数a=
.
展开式中的x3项的系数为20,则非零实数a=
.
15.△ABC顶点在以x轴为对称轴,原点为焦点的抛物线上,已知A(-6,8),且△ABC
的重心在原点,则过B、C两点的直线方程为 .
16.设正数数列{an}的前n项和为Sn,且存在正数t,使得对于所有的自然数n,有
![]() 成立,若
成立,若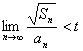 ,则t的取值范围是
.
,则t的取值范围是
.
三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤.
| |
设复数![]() 且
且![]() .
.
求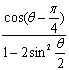 的值.
的值.
| |
18.(理)(本题满分共12分)
 已知正三棱柱ABC—A1B1C1的每条棱长均为a,M为
已知正三棱柱ABC—A1B1C1的每条棱长均为a,M为
棱A1C1上的动点.
(Ⅰ)当M在何处时,BC1//平面MB1A,并证明之;
(Ⅱ)在(I)下,求平面MB1A与平面ABC所成的二
面角的大小;
(Ⅲ)求B—AB1M体积的最大值.
18.(文)(图同理18,本题满分12分)
已知正三棱柱ABC—A1B1C1的每条棱长均为a,M为
棱A1C1的中点
(Ⅰ)求证BC1//平面MB1A;
(Ⅱ)求平面MB1A与平面ABC所成的二面角的正切值;
(Ⅲ)求B—AMB1的体积.
| |
设常数![]() 不等式
不等式![]() 的解集为M
的解集为M
(Ⅰ)当ab=1时,求解集M;
(Ⅱ)当M=(1,+∞)时,求出a,b应满足的关系.
19.(文)(本题满分12分)
已知函数![]() (其中a>0,且a≠1),解关于x的不等式
(其中a>0,且a≠1),解关于x的不等式
![]()
| |
20.(本题满分12分)
一家企业生产某种产品,为了使该产品占有更多的市场份额,拟在2001年度进行一系列的促销活动,经过市场调查和测算,该产品的年销量x万件与年促销费用t万元之间满足:
3-x与t+1(t≥0)成反比例,如果不搞促销活动,该产品的年销量只能是1万件,已知2001年生产该产品的固定投资为3万元,每生产1万件该产品需再投资32万元,当该产品的售价g(x)满足![]() 时,则当年的产销量相等.
时,则当年的产销量相等.
(Ⅰ)将2001年的利润y表示为促销费t万元的函数;
(Ⅱ)该企业2001年的促销费投入多少万元时,企业的年利润最大?
(注:利润=收入-生产成本-促销费)
21.(本题满分12分)

A、B是两个定点,且AB=8,动点M到A点的距离
是10,线段MB的垂直平分线l交MA于点P,若以AB
所在直线为x轴,AB的中垂线为y轴建立直角坐标系.
(Ⅰ)试求P点的轨迹c的方程;
(Ⅱ)直线![]() 与点P所在
与点P所在
曲线c交于弦EF,当m变化时,试求△AEF的面积的最大值.
| |
22.(本题满分14分)
已知函数f(x)在(-1,1)上有定义,![]() 且满足x、y∈(-1,1) 有
且满足x、y∈(-1,1) 有
![]() .
.
(Ⅰ)证明:f(x)在(-1,1)上为奇函数;
(Ⅱ)对数列![]() 求
求![]() ;
;
(Ⅲ)(理)求证![]()
(文)求证![]()
高考模拟测试6
数学试题参考答案
一、选择题(理)CBACD DCBCD AB
(文)CBACD DCBCD AB
二、填空题
(13)14π (14)5 (15)![]() (16)
(16)![]()
三、解答题
17.解:![]() (2分)
(2分)
即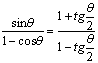 即
即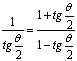
即![]() (6分)
(6分)
![]()
![]() (8分)
(8分)

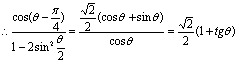
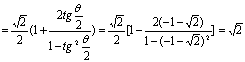
即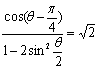 (12分)
(12分)
18.(理)解:(I)当M在A1C1中点时,BC1//平面MB1A
∵M为A1C1中点,延长AM、CC1,使AM与CC1延
长线交于N,则NC1=C1C=a
连结NB1并延长与CB延长线交于G,
则BG=CB,NB1=B1G (2分)
在△CGN中,BC1为中位线,BC1//GN
又GN![]() 平面MAB1,∴BC1//平面MAB1 (4分)
平面MAB1,∴BC1//平面MAB1 (4分)
(II)∵△AGC中, BC=BA=BG ∴∠GAC=90°
即AC⊥AG 又AG⊥AA1 ![]()
![]() (6分)
(6分)
∴∠MAC为平面MB1A与平面ABC所成二面角的平面角
![]()
∴所求二面角为![]() (8分)
(8分)
(Ⅲ)设动点M到平面A1ABB1的距离为hM.
![]()
即B—AB1M体积最大值为![]() 此时M点与C1重合. (12分)
此时M点与C1重合. (12分)
18.(文)(Ⅰ)同(理)解答,见上
(Ⅱ)同理科解答:设所求二面角为θ,则![]()
(Ⅲ)![]()
19.(理)解:(I)首先![]() 即
即![]() 即
即![]()
![]() (3分)
(3分)
得![]() 解得
解得![]() (舍去)或
(舍去)或![]()
![]()
![]() (6分)
(6分)
(II)令![]() ,先证
,先证![]() 时为单调递增函数
时为单调递增函数
![]()
![]()
![]() 得证 (8分)
得证 (8分)
欲使解集为(1,+∞),只须f(1)=1即可,即a-b=1,∴a=b+1 (12分)
19.(文)解:![]() 可知0<a<1 (4分)
可知0<a<1 (4分)
∴不等式![]() (8分)
(8分)
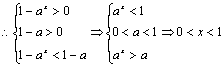
∴原不等式的解集为{x0<x<1} (12分 )
20.解:(I)由题意得![]() (2分)
(2分)
![]()
从而生产成本为![]() 万元,年收入为
万元,年收入为
![]() (4分)
(4分)
![]() (6分)
(6分)
![]()
∴年利润为y![]() (8分)
(8分)
(II)y![]() (万元)
(万元)
当且仅当![]() (12分)
(12分)
∴当促销费定为7万元时,利润最大.
21.解(I)以AB所在直线为x轴,AB中垂线为y轴,则A(-4,0),B(4,0)
PA+PB=PA+PM=10 (2分)
∴2a=10 2c=8 ∴a=5,c=4
∴P点轨迹为椭圆![]() (4分)
(4分)
(II)![]() 过椭圆右焦点B(4,0)
过椭圆右焦点B(4,0)
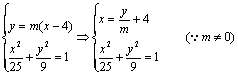
![]()
整理得![]() (6分)
(6分)
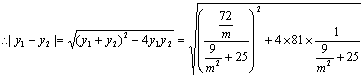
![]() *(8分)
*(8分)
∵m为直线的斜率,∴可令m=tgθ代入*得
![]()
![]()
当且仅当![]()
即![]() 时,
时,![]()
![]() (12分)
(12分)
22.证:(I)令![]() 则
则![]()
令![]() 则
则![]() 为奇函数 (4分)
为奇函数 (4分)
(II)![]() ,
, ![]()
![]() 是以-1为首项,2为公比的等比数列.
是以-1为首项,2为公比的等比数列.
![]() (4分)
(4分)
(III)(理)![]()
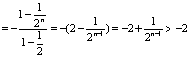
而![]()
![]() (6分)
(6分)
(III)(文)![]()