高考数学串讲（一） 函数
一，基础知识
1，函数的基本性质：
（1）函数的单调性：①
（或
）
单调递增（或单调递减）；
②单调递增（或单调递减）
（或
）。
（2）函数的周期性：
，则称
为的一个为期；若
是所有
周期中一个最小的正周期，则称的周期是。
（3）函数的奇偶性：①
是偶函数；
②
是奇函数。（注：定义域需关于原点对称）。
（4）函数的连续性：在
处连续
（常数）。
（5）函数图像的对称性：若
满足
的图像
关于直线
对称。
2，函数的图像：①
，②
，③
，④
，
⑤
，⑥
，⑦
，⑧
的图像。
3，函数的定义域与值域：
①定义域与值域的关系：
与
互换；
②极值：
是的一个极值
；
③最值：(i)对于定义域D内的任意,存在
,使得
,则
;
对于定义域D内的任意,存在,使得
,则
(ii)在闭区间
内连续,则必有最大值与最小值.
(iii) 
恒成立
或
4，根的分布：若在闭区间内连续，且
，
则至少存在一点
，使得
。
二，跟踪训练
1，（04广东）设函数
。
（I）证明：当
，且
时，
；
（II）点P（
）（
）在曲线上，求曲线在点P处的切线与轴
和轴的正向所围成的三角形面积表达式（用表示）。
2，（04广东）设函数
，其中常数
为整数。
（I）当为何值时，
；
（II）定理：若函数
在上连续，且
与
异号，则至少存在一点
，使
。
试用上述定理证明：当整数
时，方程
在
内有两个实根。
3，（05广东）设函数在
上满足
，
，
且在闭区间
上，只有
。
（I）试判断函数的奇偶性；
（II）试求方程在闭区间
上的根的个数，并证明你的结论。
4，（05全国III）已知函数
。
（I）求的单调区间和值域；
（II）设
，函数
。若对于任意
，总存在
，使得
成立，求
的取值范围。
5，（05辽宁）函数在区间
内可导，导函数
是减函数，且。
设
，
是曲线在点
处的切线方程，并设函数
。
（I）用，
，
表示；
（II）证明：当
时，
；
三，简明提示
1，（I）由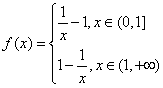
，
，
可证。
（II）切线方程为
，
。
2，（I）
，由
，得
；
（II）由，
，
，及
可证。
3，（I）
是的对称轴，若是奇函数，有
=
，与在上只有矛盾！同理可知它也不是
偶函数；得是非奇非偶函数。
（II）由
，又在上只有，知在
上只有2个解，在
上只有
个解，在
上只有400个解，共802个解。
4，（I）当
时，是减函数；当
时，是增函数。
的值域是
。
（II）当
时，，有为减函数，
，
又
，则
，得
。
5，（I）
；
（II）令
，得
；