直线与圆高考题

第十一章　直线

考试内容：

有向线段.两点间的距离.线段的定比分点.

直线的方程.直线的斜率.直线的点斜式、斜截式、两点式、截距式方程.直线方程的一般式.

两条直线平行与垂直的条件.两条直线所成的角.两条直线的交点.点到直线的距离.

考试要求：

(1)理解有向线段的概念.掌握有向线段定比分点坐标公式.熟练运用两点间的距离公式和线段的中点坐标公式.

(2)理解直线斜率的概念，掌握过两点的直线的斜率公式.熟练掌握直线方程的点斜式，掌握直线方程的斜截式、两点式、截距式以及直线方程的一般式.能够根据条件求出直线的方程.

(3)掌握两条直线平行与垂直的条件，能够根据直线的方程判定两条直线的位置关系.会求两条相交直线的夹角和交点.掌握点到直线的距离公式.

一、选择题

1.　　　 (90(7)3分)如果直线y＝ax＋2与直线y＝3x－b关于直线y＝x对称，那么
A.a＝，b＝6　　　　B.a＝，b＝－6　 C.a＝3，b＝－2　　 D.a＝3，b＝6

2.　　　 (90上海)设点P在有向线段的延长线上，P分所成的比为λ，则
A.λ＜－1　　　　　　B.－1＜λ＜0　　　C.0＜λ＜1　　　　 D.λ＞1

3.　　　 (90广东)如果直线ax＋2y＋1＝0与直线x＋y－2＝0互相垂直，那么a的值等于
A.1　　　　　　　　　B.－　　　　　　C.－　　　　　　 D.－2

4.　　　 (91(10)3分)如果AC＜0且BC＜0，那么直线Ax＋By＋C＝0不通过第象限
A.一　　　　　　　　 B.二　　　　　　　C.三　　　　　　　 D.四

5.　　　 (91三南)点(4,0)关于直线5x＋4y＋21＝0的对称点是
A.(－6,8)　　　　　　B.(－8,－6)　　　 C.(6,8)　　　　　　D.(－6,－8)

6.　　　 (92(13)3分)已知直线l₁和l₂夹角的平分线为y＝x，如果l₁的方程是ax＋by＋c＝0(ab＞0)，那么l₂的方程是
A.bx＋ay＋c＝0　　　 B.ax－by＋c＝0　　C.bx＋ay－c＝0　　 D.bx－ay＋c＝0

7.　　　 (93(5)3分)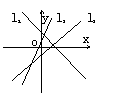直线bx＋ay＝ab(a＜0，b＜0)的倾斜角是
A.arctg(－)　　　 B.arctg(－)　　 C.π－arctg　　　D.π－arctg

8.　　　 (95(5)4分)若图中的直线l₁，l₂，l₃的斜率分别为k₁，k₂，k₃，则
A.k₁＜k₂＜k₃　 B.k₃＜k₁＜k₂　 C.k₃＜k₂＜k₁　 D.k₁＜k₃＜k₂

9.　　　 (95上海)下列四个命题中的真命题是
A.经过点P(x₀，y₀)的直线一定可以用方程y－y₀＝k(x－x₀)表示；
B.经过任意两个不同点P₁(x₁，y₁)、P₂(x₂，y₂)的直线都可以用方程
(y－y₁)(x₂－x₁)＝(x－x₁)(y₂－y₁)表示；
C.不经过原点的直线都可以用方程＝1表示；
D.经过顶点A(0，b)的直线都可以用方程y＝kx＋b表示

10.　  (96上海)过点(4,0)和点(0,3)的直线的倾斜角为
A.arctg　　　　　 B.π－arctg　　 C.arctg(－)　　　D.π－arctg(－)

11.　  (97(2)4分)如果直线ax＋2y＋2＝0与直线3x－y－2＝0平行，那么系数a＝
A.－3　　　　　　　　B.－6　　　　　　 C.－　　　　　　 D.

12.　  (98(4)4分)两条直线A₁x＋B₁y＋C₁＝0，A₂x＋B₂y＋C₂＝0垂直得充要条件是
A.A₁A₂＋B₁B₂＝0　　　　B.A₁A₂－B₁B₂＝0　　　C.＝－1　　　 C.＝1

13.　  (98上海)设a，b，c分别是△ABC中∠A，∠B∠C所对边的长，则直线sinA·x＋ay＋c＝0与bx－sinB·y＋sinC＝0的位置关系是
A.平行　　　　　　　 B.重合　　　　　　C.垂直　　　　　　 D.相交但不垂直

14.　  (99(9)4分)直线x＋y－2＝0截圆x²＋y²＝4所得的劣弧所对的圆心角为
A.　　　　　　　　B.　　　　　　　C.　　　　　　　 D.

15.　　 (2000⑽5分)过原点的直线与圆x²＋y²＋4x＋3＝0相切，若切点在第三象限，则该直线的方程是
A.y＝x　　　　　　B.y＝－x　　　 C.y＝x　　　　　D.y＝－x

16.　　 (2001(2)5分)过点A(1，-1)，B(-1，1)且园心在直线x+y-2=0上的圆的方程是

A．(x-3)²+(y+1)²=4　B．(x+3)²+(y-1)²=4　C．(x-1)²+(y-1)²=4　　D．(x+1)²+(y+1)²=4

17．（2001上海(14)5分）若直线的倾斜角为，则（　　）
　　A．等于0　　　　B．等于　　　 C．等于　　　 D．不存在

二、填空题

1.　　 (90上海)过点(1，2)且与直线2x＋y－1＝0平行的直线方程是____________

2.　　 (92上海)如果直线l与直线x＋y－1＝0关于y轴对称，那么直线l的方程是________

3.　　 (93上海)点P分所成的比是－3，则B点分所成的比是_________

4.　　 (96上海)已知O(0,0)和A(6,3)两点，若点P在直线OA上，且，又P是线段OB的中点，则点B的坐标为___________

5.　　 (2000上海(1)4分)已知向量＝{－1，2}，＝{3，m}，若，则m＝_______

6.　　 (2001上海(6)4分)圆心在直线上且与轴相切于点（1，0）的圆的方程为________．

三、解答题

1.　　 (89上海)在直角坐标系中，过点P(－3，4)的直线l与直线OP夹角为45°，求直线l的方程

2.　　 (94上海)在直角坐标系中，设矩形OPQR的顶点按逆时针顺次为O(0,0),P(1,t),Q(1－2t,2＋t),R(－2t,2),其中t∈(0,＋∞)
⑴求矩形OPQR在第一象限部分的面积S(t)；
⑵确定函数的单调取减，并加以证明