高考数学仿真试题（一）

2004-2005届高考数学仿真试题（一）（广东）

命题：廖美东　　　　　　　　  考试时间：2005-4-1

本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟.

注意事项：

1.答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目、试卷类型(A或B)用铅笔涂写在答题卡上.

2.每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，不能答在试题卷上.

3.考试结束，监考人将本试卷和答题卡一并收回.

参考公式：

如果事件A、B互斥，那么　　　　　　　　　　　　　  正棱锥、圆锥的侧面积公式

P（A+B）=P（A）+P（B）　　　　　　　　　　　 

如果事件A、B相互独立，那么　　　　　　　　　　　  其中c表示底面周长，l表示斜

P（AB）=P（A）P（B）　　　　　　　　　　　  高或母线长

如果事件A在一次试验中发生的概率是　　　　　　　　 球的体积公式

P，那么n次独立重复试验中恰好发生k次的概率　　　　

　　　　　　　　　　　　　　  其中R表示球的半径

第Ⅰ卷（选择题　共50分）

一、选择题（本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1.已知直线l₁:x+ay+1=0与直线l₂:x－2y+2=0垂直，则a的值为

A.2　　　　　　　　 B.－2　　　　　　　　　　　　　 C.－ 　　　　　　　　　　　 D.

2.函数y=sin（x+θ）cos（x+θ）在x=2时有最大值，则θ的一个值是

A.　　　　　　　　　　　　　 B.　　　　　　　　　　　　　 C. 　　　　　　　　　　　 D.

3.已知直二面角α—l—β，A∈α，B∈β，AB⊥l，AB=6，则线段AB的中点到l的距离为

A.1　　  　　　　　　　　　　B.2　　　　　　　　　　　　　　　C.3　　　　　　　　　　　　　D.不能确定

4.已知等差数列{a_n}的前20项的和为100，那么a₇·a₁₄的最大值为

A.25　　  　　　　　　　　　B.50　　　　　　　　　　　　　　 C.100　　　　　　　　　　　D.不存在

5.设函数f（x）是定义在R上且以3为周期的奇函数，若f（2）=1，f（1）=a，则

A.a=2　　　　　　　　　　　B.a=－2　　　　　　　　　　　 C.a=1　　　　　　　　　　　D.a=－1

6.已知一个简单多面体的各个面都是三角形，则顶点数V与面数F满足的关系是

A.2V+F=4　　　　　　　 B.2V－F=4　　　　　　　　　 C.2V+F=2　　　　　　　 D.2V－F=2

7.若函数y=sin（x+）+2的图象按向量a平移后得到函数y=sinx的图象，则a等于

A.（－，－2）　　　　　　　　　　　　　　　　　　　B.（，2）

C.（－，2） 　　　　　　　　　　　　　　　　　　　　 D.（，－2）

8.6名同学排成两排，每排3人，其中甲排在前排的概率是

A. 　　　　　　　　　　　　B.　　　　　　　　　　　　　　C. 　　　　　　　　　　　　　D.

9.如果直线ax+by=4与圆C：x²+y²=4有两个不同的交点，那么点（a，b）和圆C的位置关系是

A.在圆外　　　　　　　　 B.在圆上　　　　　　　　　　　C.在圆内　　　　　　　　 D.不能确定

10.函数f（x）=ax²+bx+c（a≠0）的定义域分成四个单调区间的充要条件是

A.a>0且b²－4ac>0　　　　　　　　　　　　　　　　　　 B.－>0　　

C.b²－4ac>0　　　　　　　　　　　　　　　　　　　　　　　 D.－<0

第Ⅱ卷（非选择题　共100分）

二、填空题（本大题共4小题，每小题5分，共20分.把答案填在题中横线上）

11.若（3a+b）ⁿ的展开式的系数和等于（x+y）⁸的展开式的系数和，则n=______.

12.过曲线y=x³－x上点（1，0）的切线方程的一般式是______.

13.已知函数f（x）=2sinωx（ω>0）在［0，］上单调递增，则ω的取值范围是______.

14.对于任意定义在R上的函数f（x），若存在x₀∈R满足f（x₀）=x₀，则称x₀是函数

f（x）的一个不动点.若函数f（x）=x²+ax+1没有不动点，则实数a的取值范围是______.

三、解答题（本大题共6小题，共80分.解答应写出文字说明、证明过程或演算步骤）

15.（本小题满分12分）甲、乙两名篮球运动员，甲投篮的命中率为0.6，乙投篮的命中率为0.7，两人是否投中相互之间没有影响，求：

（1）两人各投一次，只有一人命中的概率；

（2）每人投篮两次，甲投中1球且乙投中2球的概率.

16.（本小题满分12分）已知函数f（x）=log₂（x+m），且f（0）、f（2）、f（6）成等差数列.

（1）求实数m的值；

（2）若a、b、c是两两不相等的正数，且a、b、c成等比数列，试判断f（a）+f（c）与2f（b）的大小关系，并证明你的结论.

17.（本小题满分13分）在△ABC中，a、b、c分别为角A、B、C的对边，且，

（1）求角A的度数；

（2）若a=，b+c=3，求b和c的值.

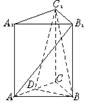18.（本小题满分13分）如图，已知正三棱柱ABC—A₁B₁C₁中，过BC₁的平面BC₁D∥AB₁，平面BC₁D交AC于D.

（1）求证BD⊥平面ACC₁A₁；

（2）若二面角C₁—BD—C等于60°，求平面BC₁D与平面BCC₁B₁所成二面角的大小.（结果用反三角函数表示）

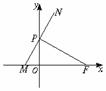19.（本小题满分14分）如图，点F（a，0）（a>0），点P在y轴上运动，M在x轴上，N为动点，且0.

（1）求点N的轨迹C的方程；

（2）过点F（a，0）的直线l（不与x轴垂直）与曲线C交于A、B两点，设点K（－a，0），与的夹角为θ，求证：0<θ<.

20.（本小题满分16分）已知a≥，f（x）=－a²x²+ax+c.

（1）证明对任意x∈［0，1］，f（x）≤1的充要条件是c≤;

（2）已知关于x的二次方程f（x）=0有两个实根α、β，证明：α≤1且β≤1的充要条件是c≤a²－a.

2004-2005届高考数学仿真试题（一）（广东）

参考答案

一、1.D　2.A  3.C　4.A　5.D  6.B　7.D　 8.B　9.A  10.C

二、11.4　12.2x－y－2=0　13.（0，　 14.（－1，3）

三、15.（1）P₁=0.6（1－0.7）+（1－0.6）0.7=0.46.　　 6分

（2）P₂=［0.6（1－0.6）］·［（0.7）²（1－0.7）⁰］=0.2352.　12分

16.（1）由f（0）、f（2）、f（6）成等差数列，

可得2log₂（2+m）=log₂m+log₂（6+m），

即（m+2）²=m（m+6）且m>0，解得m=2.　　 6分

（2）由f（x）=log₂（x+2），可得2f（b）=2log₂（b+2）=log₂（b+2）²，

f（a）+f（c）=log₂（a+2）+log₂（c+2）=log₂［（a+2）（c+2）］， 8分

∵a、b、c成等比数列，∴b²=ac，　　9分

又a、b、c是两两不相等的正数，

故（a+2）（c+2）=ac+2（a+c）+4>ac+4+4=b²+4b+4=（b+2）²，　　　10分

∴log₂［（a+2）（c+2）］>log₂（b+2）²，即f（a）+f（c）>2f（b）　　 12分

17.（1）由已知得2［1－cos（B+C）］－（2cos²A－1）=，　　2分

∵cos（B+C）=－cosA，　　3分

∴4cos²A－4cosA+1=0，

∴（2cosA－1）²=0，即cosA=.　　5分

∴A=60°.　　 6分

（2）∵a²=b²+c²－2bccosA=b²+c²－bc=（b+c）²－3bc，

∵a=，b+c=3，　　　8分

∴3=9－3bc，∴bc=2，　10分

由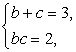解之得或.　13分

18.（1）连结B₁C交BC₁于O，则O是B₁C的中点，连结DO，

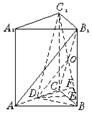∵AB₁∥平面BC₁D，AB₁平面AB₁C，

平面AB₁C∩平面BC₁D=DO，

∴AB₁∥DO，　　　 3分

∴D是AC的中点，

∵△ABC是正三角形，∴BD⊥AC，

∵平面ACC₁A₁⊥平面ABC，

∴BD⊥平面ACC₁A₁.　 6分

（2）∵CC₁⊥平面ABC，且CD⊥BD，

∴C₁D⊥BD，

∴∠C₁DC是二面角C₁—BD—C的平面角，　　8分

∴∠C₁DC=60°，

设正三棱柱底边长为2，则DC=1，CC₁=，

作DE⊥BC于E，

∵平面BCC₁B₁⊥平面ABC，

∴DE⊥平面BCC₁B₁，

作EF⊥BC₁于F，连结DF，则DF⊥BC₁，

∴∠DFE是平面BC₁D与平面BCC₁B₁所成二面角的平面角，　　 10分

在Rt△DFE中，DE=，

在Rt△DFE中，EF=BE·sinC₁BC=，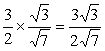

∴tanDFE=，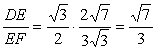

∴平面BC₁D与平面BCC₁B₁所成二面角的大小为arctan.　　 13分

19.（1）（方法一）设N（x，y），∵=0，即P是MN的中点，

∴M（－x，0），P（0，），　 2分

∵=0，∴PM⊥PF，　4分

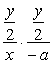∴=－1，

∴y²=4ax即为所求.　　　6分

（方法二）设N（x，y），M（x₀，0），P（0，y₀）

则　　　　　　2分

由·=0，得ax₀+y₀²=0，　　 ①

由+=0，得（x+x₀，y－2y₀）=0，　　 4分

即∴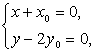

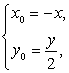
代入①得，y²=4ax即为所求.　　　6分

（2）设l的方程为y=k（x－a），

由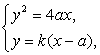消去x，得y²－y－4a²=0，　　　　 8分

设A（x₁，y₁），B（x₂，y₂），则y₁y₂=－4a²，　　　　 9分

=（x₁+a，y₁），=（x₂+a，y₂），　　　　 10分

·=（x₁+a）（x₂+a）+y₁y₂=x₁x₂+a（x₁+x₂）+a²+y₁y₂

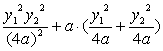=+a²－4a²

=（y₁²+y₂²）－2a²>（2y₁y₂）－2a²

=×4a²－2a²=0，

∴cosθ=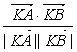>0，

∴0<θ<.　　　　　14分

20.（1）f（x）=－a²（x－）²+c+，

∵a≥，∴∈（0，1，

∴x∈（0，1时，［f（x）］_max=c+，　　　　　　2分

若c≤，则f（x）≤［f（x）］_max=c+≤1，　　　4分

若f（x）≤1，则［f（x）］_max=c+≤1，即c≤，

∴对任意x∈［0，1］，f（x）≤1的充要条件是c≤.　　　　6分

（2）（方法一）方程－a²x²+ax+c=0的两根为, 9分

不妨设，其中1+4c≥0，若c≤a²－a，

则1+4c≤4a²－4a+1=（2a－1）²，

∵2a－1≥0，∴≤2a－1，

即0<≤1，即α≤1，　11分

又1－≥1－（2a－1）=2－2a>－2a，

∴>－1，

又∵≤≤1，

∴β≤1.　　　10分

若α≤1，且β≤1，

∴≤1，且≥－1，

∵2a≥1，

∴≤2a－1，且≤2a+1，　　 13分

∴≤2a－1，

即c≤a²－a，　　　 13分

∴α≤1且β≤1的充要条件是c≤a²－a.　　 16分

（方法二）∵a≥，∴∈（0，1［－1，1］　 9分

又抛物线开口向下，

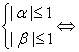∴f（x）=0的两根在［－1，1］内， 12分

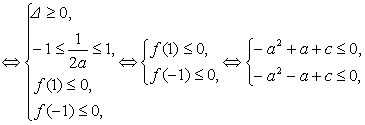　　　 14分

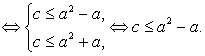　　　　　　16分