高考创新思维题型速递
广东省中山市东升高中 高建彪
创新是一个民族的灵魂，创新意识在高考卷中常呈现于一道新颖小题，它需要对新颖的信息、情景与设问，选择有效的方法和手段分析信息，综合与灵活应用数学知识、思想和方法，提高创新思维能力，下面将近期的各地区创新试题进行归类学习.
一、运算定义型：
例1.（05年襄樊.1月调研16）对任意实数x、y，定义运算
＝ax＋by＋cxy，其中a、b、c为常数，等号右边的运算是通常意义的加、乘运算．现已知1*2＝3，2*3＝4，且有一个非零实数m，使得对任意实数x，都有
，则m＝ ．（4）
【解】
点评：定义一种新的运算规则，我们首先要理解规则的含义并直接按规则进行运算，即用“代入法”进行运算. 这里还考查了恒等式的处理，即合并后各项系数为0，也体现了方程思想与待定系数法的运用.
练1.（05年南京师大附中.质检15）定义一种运算“※”，对任意正整数n满足：（1）1※1=3，（2）(n+1)※1=3+n※1，则2004※1的值为 ．
练2.（05年虹口.1月质检）定义集合A，B的一种运算“*”，A*B={pp=x+y，xÎA，yÎB}。若A={1,2,3}，B={1,2}，则集合A*B中所有元素的和=________.
练3.（05年惠州.调研9）编辑一个运算程序：1&1 = 2 , m&n = k , m&(n + 1) = k + 2，则 1&2005 的输出结果为（ ）.
A. 4008 B. 4006 C. 4012 D. 4010
二、找寻规则型：
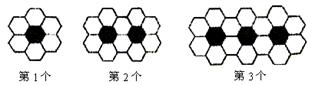例2.（05年惠州.二研16）黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案：
则第n个图案中有白色地面砖 块.
【解】
点评：对所给出的已知条件进行观察与分析，找出存在的规律. 此题的规律是构成等差数列，关键是比较相邻的两个图形，找出公差.
练4.（05年虹口.1月质检）一个七位电话号码a1a2a3a4a5a6a7，如果前面三位数码a1a2a3的顺序与a4a5a6或a5a6a7相同(可能三者都一样)，则称此号码为“可记忆的”. 如果a1,a2,…,a7可取数码0,1,2,…,9中的任一个，则不同的“可记忆的”号码共有 个.
练5.（05年南京师大附中.质检16）一同学在电脑中打出如下若干个圆（图中●表示实圆，○表示空心圆）：●○●●○●●●○●●●●○●●●●●○……若将此若干个圆依次规律继续下去得到一系列圆，那么在前2004个圆中有 个空心圆.
练6.（05年江苏东海中学质检.12）一个机器猫每秒前进或后退一步，程序设计人员让机器猫以每前进3步，然后再后退2步的规律移动；如果将此机器猫放在数轴的原点上，面向正的方向，以1步的距离为1个单位长，令P（n）表示第n秒时机器猫所在的位置的坐标，且P（0）=0，那么下列结论中错误的是（ ）
A. P(3)=3 B. P(5)=1 C. P(101)=21 D. P(103)<P(104)
练7.（05年南通.九校联考16）一项“过关游戏”规则规定：在第n关要抛掷一颗骰子n次，如果这n次抛掷所出现的点数之和大于n2，则算过关，那么，连过前二关的概率是_______.
三、类比归纳型：
例3.（04年黄冈.秋调研16）当 
成等差数列时，有a0-2a1+a2=0，当
成等差数列时，有a0-3a1+3a2-a3=0，当a0，a1，a2，a3，a4成等差数列时，有a0-4a1+6a2-4a3+a4=0，由此归纳：当
成等差数列时有
,如果成等比数列，类比上述方法归纳出的等式为
．
【解】
点评：分析已知条件的规律，通过类比归纳思想，将规律转化到需探索的结论. 此题的类比归纳，既有同一个数列之间，从有限到无限的类比归纳；也有两个数列之间，从等差数列到等比数列的类比归纳.
四、函数研究型：
例4.（05年南京师大附中.质检7）拟定从甲地到乙地通话
分钟的话费由
给出，其中
是大于或等于的最小正整数，如：
，从甲地到乙地通话5.2分钟的话费是（ ）.
A．3.71 B．4.24 C．4.77 D．7.95
【解】
点评：解题关键是理解符号的概念，抓住分段函数的对应函数式.
练8.（05年1月东城区.质检13）定义“符号函数”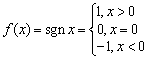 
，则不等式
的解集是
.
五、排列组合型：
例5.（05年江苏.15市模拟15）“渐减数”是指每个数字比其左边数字小的正整数（如98765），若把所有五位渐减数按从小到大的顺序排列，则第55个数为 .
【解】
点评：理解渐减数的定义，明确组成渐减数的方法。个数的计算过程中应用排列组合的计数方法进行解答.
练9.（05年朝阳区.1月质检13）将一个四棱锥的每一个顶点染上一种颜色，并使同一条棱的两端异色，若只有五种颜色可供使用，则不同的染色方法总数为 .
六、图表分析型：
例6.（04年黄冈.秋调研9）把正整数按下图所示的规律排序，则从2003到2005的箭头方向依次为（ B ）.
【解】
点评：分析所给出图形的特征，抓住其内在规律，根据规律解答项数较大的图形情况，这里的项数一般与年份接近.
练10.（05年湛江市.1月质检14）某住宅小区有居民2万户，从中随机抽取200户，调查是否安装宽带，调查结果如下表所示：
| 宽带 | 动迁户 | 原住户 |
| 已安装 | 60 | 35 |
| 未安装 | 45 | 60 |
则该小区已安装宽带的户数估计有 户.
小结语：解决创新问题，需要理解题中的新情景，发现已知条件中的规律，转化为熟悉的数学知识与数学方法求解. 创新意识是理性思维的高层次表现，对数学问题的“观察、猜测、概括、证明”，是发现问题和解决问题的重要途径，对数学知识的“迁移、组合、融会”，是较强创新意识的展现. （写于2005年2月27日）
答案：例1～6. 4；
；
；B；76542；B
练1～5. 6012；14；D；19990；61；
练6～10. D ；
；
；420；9500
高考创新思维题型速递
一、运算定义型：
例1.（05年襄樊.1月调研16）对任意实数x、y，定义运算＝ax＋by＋cxy，其中a、b、c为常数，等号右边的运算是通常意义的加、乘运算．现已知1*2＝3，2*3＝4，且有一个非零实数m，使得对任意实数x，都有，则m＝ ．（4）
练1.（05年南京师大附中.质检15）定义一种运算“※”，对任意正整数n满足：（1）1※1=3，（2）(n+1)※1=3+n※1，则2004※1的值为 ．
练2.（05年虹口.1月质检）定义集合A，B的一种运算“*”，A*B={pp=x+y，xÎA，yÎB}。若A={1,2,3}，B={1,2}，则集合A*B中所有元素的和=________.
练3.（05年惠州.调研9）编辑一个运算程序：1&1 = 2 , m&n = k , m&(n + 1) = k + 2，则 1&2005 的输出结果为（ ）.
A. 4008 B. 4006 C. 4012 D. 4010
二、找寻规则型：
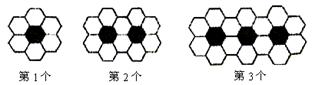例2.（05年惠州.二研16）黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案：
则第n个图案中有白色地面砖 块.
练4.（05年虹口.1月质检）一个七位电话号码a1a2a3a4a5a6a7，如果前面三位数码a1a2a3的顺序与a4a5a6或a5a6a7相同(可能三者都一样)，则称此号码为“可记忆的”. 如果a1,a2,…,a7可取数码0,1,2,…,9中的任一个，则不同的“可记忆的”号码共有 个.
练5.（05年南京师大附中.质检16）一同学在电脑中打出如下若干个圆（图中●表示实圆，○表示空心圆）：●○●●○●●●○●●●●○●●●●●○……若将此若干个圆依次规律继续下去得到一系列圆，那么在前2004个圆中有 个空心圆.
练6.（05年江苏东海中学质检.12）一个机器猫每秒前进或后退一步，程序设计人员让机器猫以每前进3步，然后再后退2步的规律移动；如果将此机器猫放在数轴的原点上，面向正的方向，以1步的距离为1个单位长，令P（n）表示第n秒时机器猫所在的位置的坐标，且P（0）=0，那么下列结论中错误的是（ ）
A. P(3)=3 B. P(5)=1 C. P(101)=21 D. P(103)<P(104)
练7.（05年南通.九校联考16）一项“过关游戏”规则规定：在第n关要抛掷一颗骰子n次，如果这n次抛掷所出现的点数之和大于n2，则算过关，那么，连过前二关的概率是_______.
三、类比归纳型：
例3.（04年黄冈.秋调研16）当 成等差数列时，有a0-2a1+a2=0，当成等差数列时，有a0-3a1+3a2-a3=0，当a0，a1，a2，a3，a4成等差数列时，有a0-4a1+6a2-4a3+a4=0，由此归纳：当成等差数列时有,如果成等比数列，类比上述方法归纳出的等式为
．
四、函数研究型：
例4.（05年南京师大附中.质检7）拟定从甲地到乙地通话分钟的话费由给出，其中是大于或等于的最小正整数，如：，从甲地到乙地通话5.2分钟的话费是（ ）.
A．3.71 B．4.24 C．4.77 D．7.95
练8.（05年1月东城区.质检13）定义“符号函数” 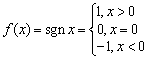，则不等式的解集是
.
五、排列组合型：
例5.（05年江苏.15市模拟15）“渐减数”是指每个数字比其左边数字小的正整数（如98765），若把所有五位渐减数按从小到大的顺序排列，则第55个数为 .
练9.（05年朝阳区.1月质检13）将一个四棱锥的每一个顶点染上一种颜色，并使同一条棱的两端异色，若只有五种颜色可供使用，则不同的染色方法总数为 .
六、图表分析型：
例6.（04年黄冈.秋调研9）把正整数按下图所示的规律排序，则从2003到2005的箭头方向依次为（ B ）.
练10.（05年湛江市.1月质检14）某住宅小区有居民2万户，从中随机抽取200户，调查是否安装宽带，调查结果如下表所示：
| 宽带 | 动迁户 | 原住户 |
| 已安装 | 60 | 35 |
| 未安装 | 45 | 60 |
则该小区已安装宽带的户数估计有 户.