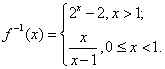2005年高考数学珠海一模考试试题
时量：120分钟 满分：150分
一、选择题：(每题5分,共50分,单选题)
1．已知集合P={-2，-1，0，1，2，3}，集合Q={x∈R
}，则P∩Q等于
（A）{-2，-1，0，1} （B）{-1，0，1 }
（C）{-1，0，1，2} （D）{-1，0，1，2，3}
2．“所有的函数都是连续的”的否命题是
（A）某些函数不是连续的 （B）所有的函数都不是连续的
（C）没有函数是连续的 （D）没有函数不是连续的
3．正方体的全面积为24，球O与正方体的各棱均相切，球O的体积是
（A）
（B）
（C）
（D）
4． 已知圆O的半径为
，圆周上两点A、B与原点O恰构成正三角形，向量
的数量积是
（A）
（B）
（C）
（D）
5．已知空间中两条不重合的直线a和b互相垂直,它们在同一平面α上的射影不可能是下面哪一种情况?
（A）两条平行直线 （B）一条直线及这条直线外一点
（C）两条相交成45°角的直线 （D）两个点
6．函数y=sinx的图象按向量a=（
，2）平移后与函数g（x）的图象重合，则
g（x）的函数表达式是
（A）cosx-2 （B）-cosx-2 （C）cosx+2 （D）-cosx+2
7．将等差数列1，4，7，10，…中的各项，按如下方式分组（按原来的次序，每组中的项数成等比数列）：1，（4，7），（10，13，16，19），（22，25，28，31，34，37，40，43），…．则2005在第几组中？
（A）第9组 （B）第10组 （C）第11组 （D）第12组
8．动点P在抛物线y2=-6x上运动,定点A(0,1),线段PA中点的轨迹方程是． 
（A）(2y+1)2=-12x （B）(2y+1)2=12x
（C）(2y-1)2=-12x （D）(2y-1)2=12x
9．在一次数学实验中, 运用图形计算器采集到如下一组数据．
| x | -2.0 | -1.0 | 0 | 1.00 | 2.00 | 3.00 |
| y | 0.24 | 0.51 | 1 | 2.02 | 3.98 | 8.02 |
则x,y的函数关系与下列哪类函数最接近?(其中a,b为待定系数)
（A）y=a+bX （B）y=a+bx （C）y=a+logbx （D）y=a+b/x
10．方程
表示的曲线所围成区域的面积是
(A)6 (B)12 (C)24 (D)48
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
二、填空题:本大题共4小题，每小题5分，共20分.把答案填在题中横线上.
11． 已知
； 
= ．
12．将边长为1的正三角形ABC沿高AD折叠成直二面角B-AD-C，则直线AC与直线AB所成角的余弦值是
13．双曲线的焦点是F1、F2，P是双曲线上一点，P到双曲线两条准线的距离之比为5︰3，∠F1PF2=120°，则双曲线的离心率是
14．已知函数f(x)=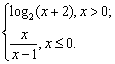 
则f-1(
)= ；f(x)的反函数
.
三、解答题:本大题共6小题，共80分.解答应写出文字说明，证明过程或演算步骤.
15．(本小题满分12分) 已知在△ABC中, 
,且三边a,b,c成等差数列,求三角形内切圆与外接圆的面积之比.
16．(本小题满分12分)
解关于x的不等式：
（0≤a＜4）
17．(本小题满分14分) 如图，直三棱柱ABC-A1B1C1中，∠ACB=90°，A1B1=2，A1C1=1，D为棱CC1中点，AB1⊥BD．
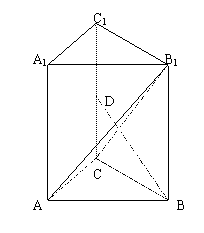1）求证：B1C⊥BD；
2）求直三棱柱体积V．
18．(本小题满分14分)某投资人打算作投资，有两个项目在考虑的范围内．据评估，甲、乙两个项目盈利的可能性分别为70%和50%，盈利率分别是40%和50%，亏损的可能性分别是15%和20%，其相应的亏损率分别为20%和15%，其余的情况是不盈不亏．投资人计划投资金额不超过20万元．
1）如果投资人在甲、乙两个项目分别投资10万元，问期望盈利是多少万元？
2）如果投资人要求确保期望盈利在4．82万元以上，问投资人对甲、乙两个项目分别投资多少万元，才能保证在两个项目都亏损的情况下，亏损额最小？
19．(本小题满分14分) 已知平面内一个定点A(1,0)和定直线l:x=-1，P是平面内一个动点，PM⊥l，垂足为M，
．
（1）求点P的轨迹方程；
（2）过A作直线QR与P的轨迹交于Q、R两点，求三角形OQR面积的最小值（O为坐标原点）．
20．(本小题满分14分) 已知数列{an}满足：
（n∈N*），a1∈（0，1）．
（1）求证：当n>1时，
；
（2）是否存在常数λ，使得对任何大于2的n，不等式
都成立？如果存在，请求出一个这样的λ值；如果不存在，请说明理由．
一模答案
BADCD DBCAC
11.
,
12. 3/4 13. 7/2(或3.5 ) 14. -1；