多面体与旋转体高考题

第十章　多面体与旋转体

考试内容：

棱柱(包括平行六面体).棱锥.棱台.多面体.

圆柱.圆锥.圆台.球.球冠.旋转体.

体积的概念与体积公理.棱柱、圆柱的体积.棱锥、圆锥的体积.棱台、圆台的体积.球和球缺的体积.

考试要求：

(1)理解棱柱、棱锥、棱台、圆柱、圆锥、圆台、球及其有关概念和性质.

(2)掌握直棱柱、正棱锥、正棱台和圆柱、圆锥、圆台、球的表面积和体积公式以及球冠的面积、球缺的体积公式(球缺体积公式不要求记忆)，并能运用这些公式进行计算.

(3)了解多面体和旋转体的概念，能正确画出直棱柱、正棱锥、正棱台、圆柱、圆锥、圆台的直观图.

(4)对于截面问题，只要求会解决与几种特殊的截面(棱柱、棱锥、棱台的对角面，棱柱的直截面，圆柱、圆锥、圆台的轴截面和平行于底面的截面，球的截面)以及已给出图形或它的全部顶点的其他截面的有关问题.

一、选择题

1. (85(1)3分)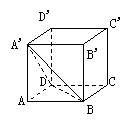如果正方体ABCD－A′B′C′D′的棱长为a，那么四面体A'－ABD的体积是
A.　　　　　　B.　　　　　　 C.　　　　　　 D.

2. (89(3)3分)如果圆锥的底半径为，高为2，那么它的侧面积是
A.4π　　　　 B.2π　　　　　C.2π　　　　　D.4π

3. (89(8)3分)已知球的两个平行截面的面积分别为5π和8π，它们位于球心的同一侧，且相距为1，那么这个球的半径是
A.4　　　　　　　　　B.3　　　　　　　 C.2　　　　　　　　　D.5

4. (90(3)3分)如果轴截面为正方形的圆柱的侧面积是S，那么圆柱的体积等于
A.　　　　　　　B.　　　　　 C.　　　　　　　D.

5. (90上海)设过长方体同一个顶点的三个面的对角线长分别为a，b，c，那么这个长方体的对角线长为
A.

6. (90广东)一个圆台的母线长是上下底面半径的等差中项，且侧面积为8πcm²,那么母线长是
A.4cm　　　　　　　　B.2cm　　　　　C.2cm　　　　　　　　D.cm

7. (91上海)设长方体对角线的长度是4，过每一顶点有两条棱与对角线的夹角都是60°，则此长方体的体积是
A.　　　　　　　B.8　　　　　　C.8　　　　　　　 D.16

8. (91上海)设正方体的全面积为24cm²,一个球内切于该正方体，那么这个球的体积是
A.πcm³　　　　　 B.πcm³　　　　　C.πcm³　　　　　　D.πcm³

9. (91三南)设正六棱锥的底面边长为1，侧棱长为，那么它的体积为
A.6　　　　　　　 B.2　　　　　　C.3　　　　　　　 D.2

10. (91三南)体积相等的正方体、球、等边圆柱(即底面直径与母线相等的圆柱)的全面积分别为S、S′、S",那么它们的大小关系是
A.S＜S′＜S"　　　　 B.S＜S"＜S′　　　C.S′＜S"＜S　　　　 D.S′＜S＜S"

11. (92(5)3分)已知轴截面是正方形的圆柱的高与球的直径相等，则圆柱的全面积与球的表面积的比是
A.6:5　　　　　　　　B.5:4　　　　　　 C.4:3　　　　　　　　D.3:2

12. (92(18)3分)长方体的全面积为11，十二条棱长之和为24，则这个长方体的一条对角线长为
A.2　　　　　　　 B.　　　　　　C.5　　　　　　　　　D.6

13.　(92上海)下列命题中的真命题是
A.各侧面都是矩形的棱柱是长方体
B.有两个相邻侧面是矩形的棱柱是直棱柱
C.各侧面都是等腰三角形的四棱锥是正四棱锥
D.有两个面互相平行，其余四个面都是等腰梯形的六面体是正四棱台

14.　(92三南)在长方体ABCD－A′B′C′D′中，若AB＝BC＝a，AA′＝2a，那么A点到直线A′C的距离等于
A.a　　　　　　 B.a　　　　　 C.a　　　　　　　 D.a

15. (92三南)有一条半径为2的弧，度数是60°,它绕过弧中点的直径旋转得一个球冠，那么这个球冠的面积是
A.4(2－)π　　　 B.2(2－)π　　 C.4π　　　　　　 D.2π

16. (92三南)若等边圆柱的体积是16πcm²，则其底面半径为
A.4cm　　　　　 B.4cm　　　　　　 C.2cm　　　　　　D.2cm

17. (93(3)3分)当圆锥的侧面积和底面积的比值是时，圆锥的轴截面顶角是
A.45°　　　　　　 B.60°　　　　　　　C.90°　　　　　　　D.120°

18.　(93(13)3分)若正棱锥的底面边长与侧棱长相等，则该棱锥一定不是
A.三棱锥　　　　　 B.四棱锥　　　　　　C.五棱锥　　　　　　D.六棱锥

19.　(93(14)3分)如果圆柱轴截面的周长l为定值，那么圆柱体积的最大值是
A.π　　　　　 B.π　　　　　　C.π　　　　　　D.

20.　(93上海)设有三个命题：
甲：底面是平行四边形的四棱柱是平行六面体；
乙：底面是矩形的平行六面体是长方体；
丙：直四棱柱是平行六面体；
以上命题中真命题的个数是：
A.0　　　　　　　　 B.1　　　　　　　 C.2　　　　　　　　D.3

21.　(94(7)4分)圆柱正六棱台的上、下底面边长分别为2和4，高为2，则其体积为
A.32　　　　　　 B.28　　　　　 C.24　　　　　　D.20

22.　(94(13)5分)圆柱过球面上A、B、C三点的截面和球心的距离等于球半径的一半，且AB＝BC＝CA＝2，则球面面积是
A.π　　　　　　 B.π　　　　　　C.4π　　　　　　　D.π

23.　(95(4)4分)正方体的全面积是a²，它的顶点都在球面上，这个球的表面积是
A.π　　　　　　 B.π　　　　　 C.2πa²　　　　　　 D.3πa²

24.　(95上海)设棱锥的底面面积为8cm²，那么棱锥的中截面(过棱锥高的中点且平行于底面的截面)的面积是
A.4cm²　　　　　　　B.2cm²　　　　　C.2cm²　　　　　　　D.cm²

25.　(96(9)4分)将边长为a的正方形ABCD沿对角线AC折起，使得BD＝a，则三棱锥D－ABC的体积为
A.　　　　　　　 B.　　　　　　 C.　　　　　　D.

26.　(96(14)5分)母线长为l的圆锥体积最大时，其侧面展开图圆心角φ等于
A.π　　　　　 B.π　　　　　C.π　　　　　　D.π

27.　(97(8)4分)长方体一个顶点上三条棱的长分别是3，4，5，且它的八个顶点都在同一个球面上，这个球的表面积是
A.20π　　　　　B.25π　　　　 C.50π　　　　　　 D.200π

28.　(97(12)5分)圆台上、下底面积分别为π、4π，侧面积为6π，这个圆台的体积是
A.π　　　　　 B.2π　　　　　C.π　　　　　 D.π

29.　(98(8)4分)已知圆锥的全面积是底面积的3倍，那么该圆锥的侧面展开图扇形的圆心角为
A.120°　　　　　　 B.150°　　　　　 C.180°　　　 D.240°

30.　(98(9)4分)如果棱台的两底面积分别为S，S'，中截面积是S0，那么
A.2　C.2S0＝S＋S'　　 D.S0²＝2SS'

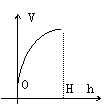
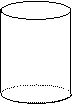
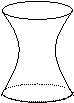
31.　(98(10)4分)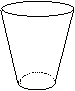向高为H的水瓶中注水，注满为止，如果注水量V与水深h的函数关系的图像如图所示，那么水瓶的形状是
A.　　　　　　　　　B.　　　　　　C.　　　　　　　 D.

32.　(98(13)分)球面上有3个点，其中任意两点的球面距离都等于大圆周长的，经过这3个点的小圆面积为4π，那么这个球的半径为
A.4　　　　　　　B.2　　　　　　C.2　　　　　　　　D.

33.　(99(7)4分)若干毫升水倒入底面半径为2cm的圆柱形器皿中，量得水面的高度为6cm，若将这些水倒入轴截面是正三角形的倒圆锥形器皿中，则水面的高度是
A.6cm　　　　　　B.6cm　　　　　　 C.2cm　　　　　 D.3cm

34.　(99(10)4分)如图，在多面体ABCDEF中，已知面ABCD是边长为3的正方形，EF∥AB，EF＝，EF与面AC的距离为2，则该多面体的体积为
A.　　　　　　　 B.5　　　　　　　 C.6　　　　　　　　D.

35.　(99(12)5分)如果圆台的上底面半径为5，下底面半径为R，中截面把圆台分成上下两个圆台，它们的侧面积之比为1:2，那么R＝
A.10　　　　　　　　B.15　　　　　　　C.20　　　　　　　 D.25

36.　(2000安徽(5)4分)一个圆锥的底面直径和高都同一个球的直径相等，那么圆锥与球的体积之比是
A.1:3　　　　　　　 B.2:3　　　　　　 C.1:2　　　　　　　D.2:9

37.　(2000⑶5分)一个长方体共一顶点的三个面的面积分别是，这个长方体对角线的长是
A.2　　　　　　　B.3　　　　　　C.6　　　　　　　　D.

38.　(2000⑼5分)一个圆柱的侧面展开图是一个正方形，这个圆柱的全面积与侧面积的比是
A.　　　　　　B.　　　　　 C.　　　　　　D.

39.　(2000⑿5分)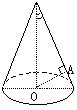如图，OA是圆锥底面中心O到母线的垂线，OA绕轴旋转一周所得曲面将圆锥分成体积相等的两部分，则母线与轴的夹角为
A.arccos　　　　B.arccos
C.arccos　　　　D.arccos

40.　(2000上海(14)4分)设有不同的直线a、b和不同的平面α、β、γ，给出下列三个命题：
⑴若a∥α，b∥α，则a∥b；　　　　　 ⑵若a∥α，a∥β，则α∥β；
⑶若α⊥γ，β⊥γ，则α∥β.其中正确命题的个数是
A.0　　　　　　　　 B.1　　　　　　　 C.2　　　　　　　　D.3

41.　(2001(3)5分)若一个圆锥的轴截面是等边三角形，其面积为，则这个圆锥的全面积是
A．6　　　　　　 B．　　　　　C．3　　　　　　 D．9

二、填空题

1.　　　 (86(13)4分)在xoy平面上，四边形ABCD的四个顶点坐标依次为(0，0)，(1，0)，(2，1)，(0，3)，则这个四边形绕x轴旋转一周所得到的几何体的体积为___________.

2.　　　 (87(15)4分)一个正三棱台的下底和上底周长分别为30cm和12cm，而侧面积等于两底面积之差，则斜高为_________.
注:满足条件“侧面积等于两底面积之差”的三棱台不存在，只有“压缩”成平面图形方可，而此时所求“斜高”实为内、外两正方形(上、下底)对应边的距离.

3.　　　 (90(20)3分)如图，三棱柱ABC－A₁B₁C₁中，若E，F分别为AB，AC中点，平面EB₁C₁F将三棱柱分成体积为V₁，V₂的两部分，那么V₁:V₂＝______.

4.　　　 (90上海)已知圆锥的中截面周长为a,母线长为l，则它的侧面积等于____

5.　　　 (91(18)3分)已知正三棱台上底面边长为2，下底面边长为4，且侧棱与底面所成的角是45°，那么这个正三棱台的体积等于________.

6.　　　 (91(20)3分)在球面上有四个点P、A、B、C，如果PA、PB、PC两两互相垂直，且PA＝PB＝PC＝a，那么这个球面的面积是_________.

7.　　　 (91上海)一个圆柱的底面直径和高都等于一个球的直径，则这个圆柱的体积与球的体积的比值为___________

8.　　　 (91三南)在体积为V的三棱柱ABC－A′B′C′中，已知S是侧棱CC′上的一点，过点S、A、B的截面截得的三棱锥的体积为V′,那么过点S、A′、B′的截面截得的三棱锥的体积为__________

9.　　　 (91三南)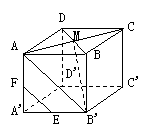已知圆台的上下底面半径分别为r、2r，侧面积等于上下底面面积之和，则圆台的高为__________

10.　　(92上海)已知圆台下底面半径为8cm,高为6cm，母线与底面成45°角，那么圆台的侧面积为_________(cm²)(结果保留π)

11.　　如(92上海)图，直平行六面体A′C的上底面ABCD是菱形，∠BAD＝60°，侧面为正方形，E、F分别为A′B′、AA′的中点，M是AC与BD的交点，则EF与B′M所成的角的大小为_________(用反三角函数表示)

12.　　(92三南)已知三棱锥A－BCD的体积为V，棱BC的长为a，面ABC和面DBC的面积分别为S、S′，设面ABC和面DBC所成二面角为α，则sinα＝_____________

13.　　(93(20)4分)在半径为30m的圆形广场上空，设置一个照明光源，射向地面的光成圆锥形，其轴截面顶角为120°，若要光源恰好照亮整个广场，其高度应为______(精确到0.1m)

14.　　(93上海)已知圆台的上下底半径分别是10cm和20cm，他的侧面展开后所得扇形的圆心角是180°,那么圆台的侧面积是______cm²(保留π)

15.　　(94(19)4分)设圆锥底面圆周上两点A、B间的距离为2，圆锥顶点到直线AB的距离为，AB和圆锥轴的距离为1，则该圆锥的体积为________.

16.　　(94上海)有一个实心圆锥体的零件，它的轴截面是边长为10cm的等边三角形，现在要在它的整个表面镀上一层防腐材料，已知每平方厘米的工料价格是0.10元，则需要费用_____元

17.　　(95(17)4分)已知圆台上、下底面圆周都在球面上，且下底面过球心，母线与底面所成的角为，则圆台的体积与球的体积之比为________.

18.　　(95上海)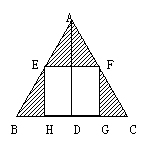把圆心角为216°，半径为5分米的扇形铁皮焊成一个锥形容器(不计焊缝)，那么容器的容积是_________立方分米(结果保留两位小数)

19.　　(96上海)如图，在正三角形ABC中，E、F分别是AB、AC的中点，AD⊥BC，EH⊥BC，FG⊥BC，D、H、G为垂足，若将正三角形ABC绕AD旋转一周所得的几何体的体积为V，则其中由阴影部分所产生的旋转体的体积与V的比值是___________

20.　　(96上海)把半径为3cm，中心角为π的扇形卷成一个圆锥形容器，这个容器的容积为_________cm³(结果保留π)

21.　　(97上海)设正四棱锥底面边长为4cm，侧面和底面所成的二面角为60°，则这个棱锥的侧面积为___________cm²

22.　　(98(18)4分)如图:在直四棱柱ABCD－A′B′C′D′中，当底面四边形ABCD满足条件_______时，有A′C⊥B′D′.(注:填上你认为正确的一种条件即可，不必考虑所有可能的情形)

23.　　(99上海)若四面体各条棱长是1或2，且该四面体不是正四面体，则其体积的值是__________(只需写出一个可能的值)

24.　　(2000安徽(16)4分)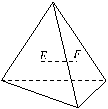右图是一体积为72的正四面体，连结两个面的重心E、F，则线段EF的长是_________.

25.　　(2000安徽(18)4分)在空间，下列命题正确的是____________.(注：把你认为正确的命题的序号都填上)
①如果两条直线a、b分别与直线l平行，那么a∥b
②如果一条直线a与平面β内的一条直线b平行，那么a∥β
③如果直线a与平面β内的两条直线b、c都有垂直，那么a⊥β
④如果平面β内的一条直线a垂直平面γ，那么β⊥γ

26.　　(2000⒃4分)如图，E、F分别为正方体的面ADD₁A₁、面BCC₁B₁的中心，则四边形BFD₁E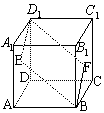在该正方体的面上的射影可能是__________________.
(要求：把可能的图的序号都填上)

27.　　(2000上海(7)4分)命题A：底面为正三角形，且顶点在底面的射影为底面中心的三棱锥是正三棱锥.命题A的等价命题B可以是：底面为正三角形，且_________的三棱锥是正三棱锥.

28.　　(2001(13)4分)若一个圆锥的轴截面是等边三角形，其面积为，则这个圆锥的侧面积是　　　　　  ．

29.　　(2001北京(13)4分)已知球内接正方体的表面积为S，那么球体积等于__________。

三、解答题

1.　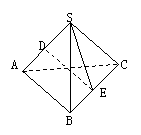　　 (87(17)12分)如图:三棱锥P－ABC中，已知PA⊥BC，PA＝BC＝l，
PA和BC的公垂线ED＝h，求证:三棱锥P－ABC的体积V＝.

2.　　　 (88(26)10分)如图:正三棱锥S－ABC的侧面是边长为a的正三角形，D是SA的中点，E是BC的中点，求△SDE绕直线SE旋转一周所得到的旋转体的体积.

3.　　　 (89(20)10分)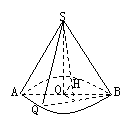如图:在平行六面体ABCD－A₁B₁C₁D₁中，已知AB＝5，AD＝4，AA₁＝3，AB⊥AD，∠A₁AB＝∠A₁AD＝.
Ⅰ.求证:顶点A₁在底面ABCD上的射影O在∠BAD的角平分线上；
Ⅱ.求这个平行六面体的体积.

4.　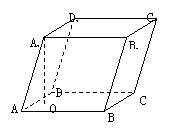　　 (91三南)已知直三棱柱ABC－A′B′C′中，∠ABC＝90°，∠BAC＝30°，BC＝1，AA′＝，M是CC′的中点，求证：AB′⊥A′M.

5.　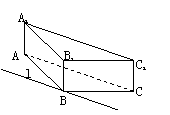　　 (92上海)圆锥的轴截面为等腰直角三角形SAB，Q为底面圆周上一点
⑴如果QB的中点为C，OH⊥SC，求证：OH⊥平面SBQ；
⑵如果∠AOQ＝60°,QB＝2，求此圆锥的体积；
⑶如果二面角A－SB－Q的大小为arctg，求∠AOQ的大小

6.　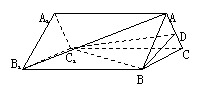　　 (93(26)8分)如图:A₁B₁C₁－ABC是直三棱柱，过点A₁，B，C₁的平面和平面ABC的交线为l.
Ⅰ.判定直线A₁C₁和l的位置关系，并加以证明；
Ⅱ.若AA₁＝1，AB＝4，BC＝3，∠ABC＝90°，求顶点A₁到
直线l的距离.

7.　　　 (94(23)12分)如图:已知A₁B₁C₁－ABC是正三棱柱，D是AC中点.
Ⅰ.证明:AB₁∥平面DBC₁；
Ⅱ.假设AB₁⊥BC₁，求以BC₁为棱DBC₁与CBC₁为面的二面角α的度数.

8.　　　 (95(23)12分)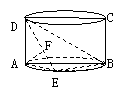如图:圆柱的轴截面ABCD是正方形，
点E在底面圆周上，AF⊥DE，F是垂足
Ⅰ.求证:AF⊥DB；
Ⅱ.如果圆柱与三棱锥D－ABC的体积比等于3π，
求直线DE与平面ABCD所成的角.

9.　　　 (95上海)四棱锥P－ABCD中，底面是矩形，AB＝3，AD＝1，又PA⊥AB，PA＝4，∠PAD＝60°
⑴求四棱锥P－ABCD的体积；
⑵求二面角P－BC－D的大小(用反三角函数表示)

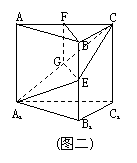
10.　　(96(22)12分)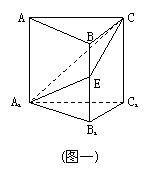如图:在正三棱柱ABC－A₁B₁C₁中，E∈BB₁，截面A₁EC⊥侧面AC₁.
Ⅰ.求证:BE＝EB₁；
Ⅱ.若AA₁＝A₁B₁，求平面A₁EC与平面所成二面角(锐角)的度数.

注意:在下面横线上填上适当内容，使之成为Ⅰ的完整证明，并解答Ⅱ.
Ⅰ.证明:在截面A₁EC内，过E作EG⊥A₁C，G是垂足，
　①∵_____________，
　　∴EG⊥侧面AC₁；取AC的中点F，连结BF，FG，
　　　由AB＝BC得BF⊥AC，
　②∵_____________，
　 ∴BF⊥侧面AC₁；得BF∥EG，
则BF，EG确定一个平面，交侧面AC₁于FG，
　③∵_____________，
 ∴BF∥FG，四边形BEGF是平行四边形，BE＝FG.
　④∵_____________，
　∴FG∥AA₁，△AA₁C∽△FGC
　⑤∵_____________，
　∴FG＝，即BE＝，故BE＝EB₁.

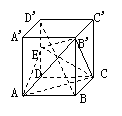
11.　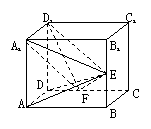　(97(23)12分)如图，在正方体ABCD－A₁B₁C₁D₁中，E，F分别是BB₁、CD的中点.
Ⅰ.证明AD⊥D₁F；
Ⅱ.求AE与D₁F所成的角；
Ⅲ.证明面AED⊥面A₁FD₁；
Ⅳ.设AA₁＝2，求三棱锥F－A₁ED₁的体积V_F－A1ED1.

12.　　(98(23)12分)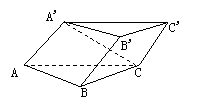已知斜三棱柱ABC－A′B′C′的侧面A′ACC′与底面ABC垂直，∠ABC＝90°，BC＝2，AC＝2 且AA′⊥A′C，AA′＝A′C.
①求侧棱AA′与底面ABC所成角的大小；
②求侧面A′ABB′与底面ABC所成二面角的大小；
 ③求顶点C到侧面A′ABB′的距离.

13.　　(99(21)12分)如图，已知正四棱柱ABCD－A′B′C′D′，点E在棱D′D上，
截面EAC∥D′B，且面EAC与底面ABCD所成的角为45°，AB＝a
(1)求截面EAC的面积
(2)求异面直线A′B′与AC之间的距离
(3)求三棱锥B′－EAC的体积

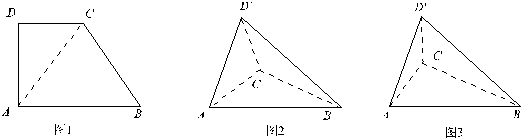
14.　　(2000安徽(20)12分)在直角梯形ABCD中，∠D＝∠BAD＝90°，AD＝DC＝AB＝a(如图1).将△ADC沿AC折起，使D到D′.记面ACD′为α，面ABC为β，面BCD′为γ.
(I)若二面角α－AC－β为直二面角(如图2)，求二面角β－BC－γ的大小；
(II)若二面角α－AC－β为60°(如图3)，求三棱锥D′－ABC的体积.

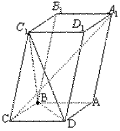
15.　　(2000⒅12分)如图，已知平行六面体ABCD－A₁B₁C₁D₁的底面ABCD是菱形，且∠C₁CB＝∠C₁CD＝∠BCD＝60°
⑴证明：C₁C⊥BD；
⑵假定CD＝2，CC₁＝，记面C₁BD为α，面CBD为β，求二面角α－BD－β的平面角的余弦值；
⑶当的值为多少时，能使A₁C⊥平面C₁BD？请给出证明.

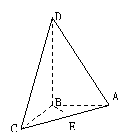
16.　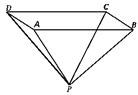(2000上海(18)12分)如图所示四面体ABCD中，AB、BC、BD两两互相垂直，且AB＝BC＝2，E是AC中点，异面直线AD与BE所成角的大小为arccos，求四面体ABCD的体积

17.　  (2001上海(19)14分)用一块钢锭浇铸一个厚度均匀，且全面积为2平方米的正四棱锥形有盖容器（如图），设容器的高为米，盖子边长为米．
　　（1）求关于的函数解析式；
　　（2）设容器的容积为立方米，则当为何值时，最大？求出的最大值．（求解本题时，不计容器的厚度）

18.　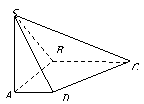  (2001w(18)12分)如图，在底面是直角梯形的四棱锥S—ABCD中，∠ABC＝90°，SA⊥面ABCD，SA＝AB＝BC＝1，AD＝．
　　(Ⅰ)求四棱锥S—ABCD的体积；
　　(Ⅱ)求面SCD与面SBA所成的二面角的正切值．