1985年——2002年部分三角函数高考试题集
一、选择题
1.
函数y=![]() sin2xcos2x是(86(4)3分)
sin2xcos2x是(86(4)3分)
A.周期为![]() 的奇函数 B.周期为
的奇函数 B.周期为![]() 的偶函数
的偶函数
C.周期为![]() 的奇函数 D.周期为
的奇函数 D.周期为![]() 的偶函数
的偶函数
2.
函数y=cosx-sin2x-cos2x+![]() 的最小值是(86广东)
的最小值是(86广东)
A.![]() B.2 C.
B.2 C.![]() D.
D.![]() E.
E.![]()
3.
函数y=cos4x-sin4x的最小正周期是(88(6),91(3)3分)
A.π B.2π C.![]() D.4π
D.4π
4. 要得到函数y=sin(2x-![]() )的图象,只须将函数y=sin2x的图象(87(6)3分)
)的图象,只须将函数y=sin2x的图象(87(6)3分)
A.向左平移![]() B.向右平移
B.向右平移![]() C.向左平移
C.向左平移![]() D.向右平移
D.向右平移![]()
5. tan70°+tan50°-![]() tan70°tan50°的值是(90广东)
tan70°tan50°的值是(90广东)
A.![]() B.
B.![]() C.-
C.-![]() D.-
D.-![]()
6. 要得到函数y=cos(2x-![]() )的图象,只需将函数y=sin2x的图象(89上海)
)的图象,只需将函数y=sin2x的图象(89上海)
A.向左平移![]() 个单位 B.向右平移
个单位 B.向右平移![]() 个单位 C.向左平移
个单位 C.向左平移![]() 个单位 D.向右平移
个单位 D.向右平移![]() 个单位
个单位
7.
函数y=![]() 的值域是(90(6)3分)
的值域是(90(6)3分)
A.{-2,4} B.{-2,0,4} C.{-2,0,2,4} D.{-4,-2,0,4}
8. 如果函数y=sin(ωx)cos(ωx)(ω>0)的最小正周期是4π,那么常数ω为(92(2)3分)
A.4 B.2 C.![]() D.
D.![]()
9.
在直角三角形中两锐角为A和B,则sinAsinB(93(6)3分)
A.有最大值![]() 和最小值0 B.有最大值
和最小值0 B.有最大值![]() ,但无最小值
,但无最小值
C.既无最大值也无最小值 D.有最大值1,但无最小值
10.
函数y=sin(2x+![]() )的一条对称轴的方程是(91(5)3分)
)的一条对称轴的方程是(91(5)3分)
A.x=-![]() B.x=-
B.x=-![]() C.x=
C.x=![]() D.x=
D.x=![]()
11.
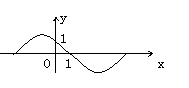 如果右图是周期为2π的三角函数y=f(x)的图像,那么f(x)可以写成(91三南)
如果右图是周期为2π的三角函数y=f(x)的图像,那么f(x)可以写成(91三南)
A.sin(1+x) B.sin(-1-x)
C.sin(x-1) D.sin(1-x)
12.
满足sin(x-![]() )≥
)≥![]() 的x的集合是(91三南)
的x的集合是(91三南)
A.{x2kπ+![]() ≤x≤2kπ+
≤x≤2kπ+![]() ,k∈Z} B.{x2kπ-
,k∈Z} B.{x2kπ-![]() ≤x≤2kπ+
≤x≤2kπ+![]() ,k∈Z}
,k∈Z}
C.{x2kπ+![]() ≤x≤2kπ+
≤x≤2kπ+![]() ,k∈Z} D.{x2kπ+π≤x≤2kπ+
,k∈Z} D.{x2kπ+π≤x≤2kπ+![]() ,k∈Z}
,k∈Z}
13. 下列函数中,最小正周期为π的偶函数是(92上海)
A.y=sin2x B.y=cos![]() C.y=sin2x+cos2x D.y=
C.y=sin2x+cos2x D.y=![]()
14.
已知集合E={θcosθ<sinθ,0≤θ≤2π=,F={θtgθ<sinθ=,那么E∩F为区间
A.(![]() ,π) B.(
,π) B.(![]() ) C.(π,
) C.(π,![]() ) D.(
) D.(![]() )
)
15.
函数y=cos(2x+![]() )的一条对称轴的方程是(93上海)
)的一条对称轴的方程是(93上海)
A.x=-![]() B.x=-
B.x=-![]() C.x=
C.x=![]() D.x=π
D.x=π
16.
设θ是第二象限的角,则必有(94(4)4分)
A.tan![]()
17.
在下列函数中,以![]() 为周期的函数是(94(6)4分)
为周期的函数是(94(6)4分)
A.y=sin2x+cos4x B.y=sin2xcos4x C.y=sin2x+cos2x D.y=sin2xcos2x
18.
函数y=4sin(3x+![]() )+3cos(3x+
)+3cos(3x+![]() )的最小正周期是(95(3)4分)
)的最小正周期是(95(3)4分)
A.6π B.2π C.![]() D.
D.![]()
19.
已知θ是第二象限的角,且sin4θ+cos4θ=![]() ,那么sin2θ等于(95(9)4分)
,那么sin2θ等于(95(9)4分)
A.![]() B.-
B.-![]() C.
C.![]() D.-
D.-![]()
20.
在下列各区间中,函数y=sin(x+![]() )的单调递增区间是(96上海)
)的单调递增区间是(96上海)
A.[![]() ,π] B.[0,
,π] B.[0,![]() ] C.[-π,0] D.[
] C.[-π,0] D.[![]() ]
]
21.
y=sin2x是(95上海)
A.最小正周期为2π的偶函数 B.最小正周期为2π的奇函数
C.最小正周期为π的偶函数 D.最小正周期为π的奇函数
22.
当-![]() 时,函数f(x)=sinx+
时,函数f(x)=sinx+![]() cosx(96(6)4分)
cosx(96(6)4分)
A.最大值是1,最小值是-1 B.最大值是1,最小值是-![]()
C.最大值是2,最小值是-2 D.最大值是2,最小值是-1
23.
函数y=sin(![]() -2x)+cos2x的最小正周期是(97(5)4分)
-2x)+cos2x的最小正周期是(97(5)4分)
A.![]() B.π C.2π D.4π
B.π C.2π D.4π
24.
函数y=cos2x-3cosx+2的最小值为(97(10)4分)
A.2 B.0 C.-![]() D.6
D.6
25.
已知点P(sinα-cosα,tanα)在第一象限,则在[0,2π]内α得取值范围是(98(6)4分)
A.(![]() ) B.(
) B.(![]() ) C.(
) C.(![]() ) D.(
) D.(![]() ,π)
,π)
26.
函数f(x)=Msin(ωx+φ)(ω>0)在区间[a,b]上是增函数,且f(a)=-M,f(b)=M,则函数g(x)=Mcos(ωx+φ)区间[a,b]上(99(4)4分)
A.是增函数 B.是减函数 C.可以取得最大值M D.可以取得最小值-M
27.
函数y=![]() 的最大值是(2000安徽(10)4分)
的最大值是(2000安徽(10)4分)
A.![]() -1 B.
-1 B.![]() +1 C.1-
+1 C.1-![]() D.-1-
D.-1-![]()
28.
设α,β是一个钝角三角形的两个锐角,下列四个不等式中不正确的是(2000安徽(12))
A.tanαtanβ<1 B.sinα+sinβ<![]()
C.cosα+cosβ>1 D.![]() tan(α+β)<tan
tan(α+β)<tan![]()
29. 已知sinα>sinβ,那么下列命题成立的是(2000⑷5分)
A.若α、β是第一象限角,则cosα>cosβ B.若α、β是第二象限角,则tanα>tanβ
C.若α、β是第三象限角,则cosα>cosβ D.若α、β是第四象限角,则tanα>tanβ
二、填空题
1. 函数y=tan![]() 的周期是____________.(87(9)4分)
的周期是____________.(87(9)4分)
2. 函数y=2sin(4x-![]() )的最小正周期是_________.(89上海)
)的最小正周期是_________.(89上海)
3. 函数y=sin(πx+2)的最小正周期是_________.(91上海)
4. 关于函数f(x)=4sin(2x+![]() )(x∈R),有下列命题:
)(x∈R),有下列命题:
①由f(x1)=f(x2)=0可得x1-x2必是π的整数倍;
②y=f(x)的表达式可以改写成y=4cos(2x-![]() );
);
③y=f(x)的图像关于点(-![]() ,0)对称;
,0)对称;
④y=f(x)的图像关于直线x=-![]() 对称.
对称.
其中正确的命题序号是_________.(注:把你认为正确的命题序号都填上)(98(19)4分)
5. 函数y=cos(![]() )的最小正周期是__________.(2000安徽(15)4分)
)的最小正周期是__________.(2000安徽(15)4分)
6. 已知sinθ-cosθ=![]() ,则sin3θ-cos3θ的值是__________.(86(16)4分)
,则sin3θ-cos3θ的值是__________.(86(16)4分)
7. 函数y=sinxcosx+sinx+cosx的最大值是___________.(90(19)3分)
8. 函数y=sinx+cosx的最大值是_________(90广东)
9. 在△ABC中,已知cosA=-![]() ,则sin
,则sin![]() =__________(90上海)
=__________(90上海)
10. 函数y=sin2x-sinxcosx+cos2x的最大值是___________(92上海)
11. 函数y=cos2(ωx)(ω>0)的最小正周期是___________(93上海)
12. 函数y=sin2x-2cos2x的最大值是___________(94上海)
13. 函数y=sin![]() +cos
+cos![]() 在(-2π,2π)内的递增区间是______________(95上海)
在(-2π,2π)内的递增区间是______________(95上海)
14. tan20°+tan40°+![]() tan20°tan40°的值是___________.(96(18)4分)
tan20°tan40°的值是___________.(96(18)4分)
15. ![]() 的值为______________.(97(18)4分)
的值为______________.(97(18)4分)
16. 函数f(x)=3sinxcosx-4cos2x的最大值是___________(97上海)
三、解答题
1. 求函数y=sin2x+2sinxcosx+3cos2x的最小值,并写出使函数y取得最小值的x的集合.(91(21)8分)
2.
已知![]() <β<α<
<β<α<![]() ,cos(α-β)=
,cos(α-β)=![]() ,sin(α+β)=-
,sin(α+β)=-![]() ,求sin2α的值.(92(25)10分)
,求sin2α的值.(92(25)10分)
3.
已知cos2α=![]() ,α∈(0,
,α∈(0,![]() ),sinβ=-
),sinβ=-![]() ,β∈(π,
,β∈(π,![]() π),求α+β(用反三角函数表示)(92上海)
π),求α+β(用反三角函数表示)(92上海)
4.
已知角α的顶点与直角坐标系的原点重合,始边在x轴的正半轴上,终边经过点P(-1,2),求sin(2α+![]() π)的值(93上海)
π)的值(93上海)
5.
已知sinα=![]() ,α∈(
,α∈(![]() ,π),tan(π-β)=
,π),tan(π-β)=![]() ,求tan(α-2β)的值(94上海)
,求tan(α-2β)的值(94上海)
6.
已知tan(![]() +θ)=3,求sin2θ-2cos2θ的值(95上海)
+θ)=3,求sin2θ-2cos2θ的值(95上海)
7.
已知sin(![]() +α)sin(
+α)sin(![]() -α)=
-α)=![]() ,α∈(
,α∈(![]() ,π),求sin4α的值(96上海)
,π),求sin4α的值(96上海)
8.
在△ABC中,a,b,c分别是A,B,C的对边,设a+c=2b,A-C=![]() ,求sinB的值.(98(20))
,求sinB的值.(98(20))
9.
在△ABC中,角A、B、C的对边分别为a、b、c.证明:![]() (2000安徽(19))
(2000安徽(19))
10. 已知函数y=![]() cos2x+
cos2x+![]() sinxcosx+1,x∈R(2000⒄12分)
sinxcosx+1,x∈R(2000⒄12分)
⑴当函数y取得最大值时,求自变量x的集合;
⑵该函数的图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到?
答案:
选择题:ACADD ABDBA DADAB ADCBB CDBBB CBDD
填空题:1.![]() 2.
2. ![]() 3.
2 4. ②③ 5. 3 6.
3.
2 4. ②③ 5. 3 6. ![]() 7.
7. ![]() 8.
8. ![]() 9.
9.![]() 10.
10. ![]()
11.![]() 12.
12. ![]() 13.
13. ![]() 14.
14. ![]() 15.
15. ![]() 16.
16.![]()
解答题:
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9. 略
10. (1)![]() ,
,![]()
(2)略