山东曲阜一中高考数学（理科）基础知识总结卷

山东曲阜一中02-03年高考数学（理科）基础知识总结卷

一、选择题（本大题共12小题，每小题5分，共60分）

1．已知集合M={x x∈N，且8-x∈N}，则M中只含二个元素的子集的个数为（　　）

A、3　　　 B、15　　　 C、21　　　　 D、42

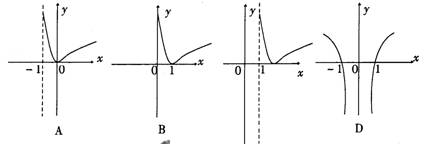
2．函数y= lg（x-1） 的图象是（　　 ）

3．若θ∈（0，），则sinθ+cosθ的一个可能值是（　　）

A、　　　　B、　　　　C、　　　　D、1

4．共轭双曲线的离心率分别为e₁，e­₂，则必有（　　）

A、=1　　　B、e₁=e₂　　C、e₁·e₂=1　　　D、=1

5．直线a⊥b，且a∥平面α，则b与平面α的关系是（　　 ）

A、bα　 B、bα　　C、b∥α或bα　 D、b与α相交或b∥α或bα

6．如果把两条异面直线看作“一对”，那么四棱锥的棱所在8条直线中，异面直线共有（　 ）

A、4　　 B、8　　　　C、16　　　 D、24

7．A=3是直线ax+2y+3a=0和直线3x+（a-1）y=a-7平行且不重合的（　 ）条件

A、充分不必要　　  B、必要不充分　　　C、充要　　　D、不充分且不必要

8．不等式组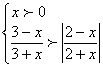的解集是（　　）

A、{x 0＜x＜3｝　　B、{x 0＜x＜}　 C、{x 0＜x＜2.5｝　D、{x 0＜x＜2｝

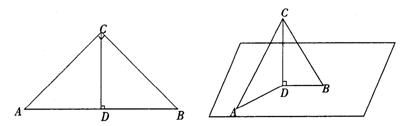
9．如图，等腰直角△ABC，沿其斜边AB上的高CD对折，使△ACD与△BCD所在平面垂直，此时，∠ACB等于（　 ）

A、45°　　　 B、60°　　　　C、90°　　　　 D、120°

10．复数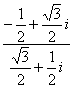的值是（　　）

A、i　　　　B、1　　　　 C、-i　　　 D-1

11．关于x的方程x²+（a²-1）x+（a-2）x=0的一个根比1大，另一根比1小，则有（　　）

A、-2＜a＜1　　　B、-1＜a＜1　　 C、a＜-2或a＞1　　　D、a＜-1或a＞2

12．f（x）=log₂（-x）++2，若f（a）=5，则f（-a）等于（　　）

A、-5　　　 B、5　　　C、7　　　　　 D、-1

二、填空题（本大题共4小题，每小题4分，共16分）

13．椭圆短轴长是2，长轴是短轴的2倍，则椭圆中心到其准线距离为　　　　　  。

14．设f（x）=，则和式=　　　　 。

15．已知数列S_n=a_n-3，那么这个数列的通项公式是　　 　　 。

16．一射手对靶射击，直到第一次命中10环，每次命中的概率为0.6，现有4颗子弹，命中后尚余子弹数目的期望为　　　　 。

三、解答题：（本大题共6小题，共74分）

17．（本题满分12分）

求函数f（x）=sin²x+cos²x+sin2x的最大值。

18．（本题满分12分）

1名技术员照看4条通讯线路，已知一天中每条线路不出现故障的概率分别为0.9、0.9、0.8、0.8，只要有一条出现故障则需一人抢修。

求：（1）线路没有故障的概率。

（2）线路至少需要2人抢修的概率。

19．（本题满分12分）

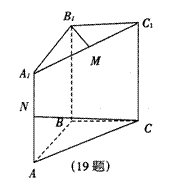如图，直三棱柱ABC—A₁B₁C₁，底面△ABC为等腰三角形，AC为斜边，AB=1，AA′=2，M、N分别为A₁C₁、A₁A的中点。

（1）求三棱锥N-B₁BC的体积。

（2）求CN与B₁M所成角的大小。

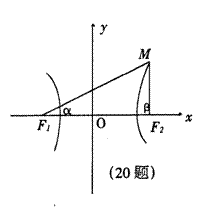20．如图，若M为双曲线x²-=1上异于顶点的任一点，又设两焦点为F₁、F₂，且∠MF₁F₂=α、=∠MF₂F₁=β，求tan、cot的值。

21．已知函数f（x）=x++1（x＞0）（k＞0）

①求函数的递增、递减区间。

②若f（x）=k+1恰有一解，求k的值。

22．已知数列{a_n}满足a₁=1，a₂=，且a_n·a_n-1+a_n+1·a_n+1（n=2、3…）求a_n。