北京海淀02-03年高考数学模拟(二)
参考公式：
三角函数的和差化积与积化和差与公式
|
其中
、S分别表示上、下底的面积，
h表示高
第Ⅰ卷（共50分）
一、选择题：本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1．在复平面内，复数
对应的向量为
.那么向量
的对应的复数是 （ ）
A．1 B．-1 C．
D．-
2．（理科学生作）
的值为 （ ）
A．
B．
C．-
D．
（文科学生作）函数
的定义域为{0，1，2，3}，那么其值域为 （ ）
A．
B．
C．
D．
3．在等比数列{an}中，
等于 （ ）
A．27 B．-27 C．81或-36 D．27或-27
4．将函数
的图象C向左平移一个单位后，得到y=f(x)的图象C1，若曲线C1关于原点对称，那么实数a的值为 （ ）
A．1 B．
C．0 D．
5．（理科学生作）在极坐标系中与圆
相切的一条直线的方程是 （ ）
A．
B．
C．
D．
（文科学生作）过点（2，1）的直线中，被
截得的最长弦所在的直线方程是 （ ）
A．
B．
C．
D．
6．将7名学生分配到甲、乙两个宿舍中，每个宿舍至少安排2名学生.那么互不相同的分配方案共有 （ ）
A．252种 B．112种 C．70种 D．56种
7．设平面
A、B∈平面
,点C∈平面
,且A、B、C均不在直线l上.给出四个命题： （ ）
①
②
③
④
其中正确的命题是 （ ）
A．①与② B．②与③ C．①与③ D．②与④
8．函数f (x)是定义域为R的偶函数，又是以2为周期的周期函数.若f (x)在[-1，0]上是减函数，那么f (x)在[2，3]上是 （ ）
A．增函数 B．减函数 C．先增后减的函数 D．先减后增的函数
9．设双曲线
的实轴长、虚轴长、焦距依次成等差数列.那么这个双曲线的离心率e等于 （ ）
A．2 B．3 C．
D．
10．设函数
上的最小值为-4，那么a的值等于 （ ）
A．4 B．-6 C．-4 D．-3
第Ⅱ卷（非选择题，共100分）
二、填空题：本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
11．将棱长为1的正方体木块加工成一个体积最大的球，那么这个球的体积为 .
12．椭圆
上到两个焦点距离之积最小的点的坐标是
.
13．不等式
的解集为
.
14．已知△ABC中，角A、B、C所对的边分别为a，b，c.若a=1,∠B=45°，△ABC的面积S=2，那么△ABC的外接圆的直径等于 .
三、解答题：本大题共6小小题，共84分.解答应写出文字说明、证明过程或演算步骤.
15．（本小题满分12分）
已知等差数列{an}的前n项和为Sn,且a2=1,S11=33,
（Ⅰ）求{an}的通项公式;
（Ⅱ）设
的值.
16．(本小题满分14分)
设在三角形ABC中,角A,B,C所对的边分别是a,b,c且满足
(Ⅰ)求证:
(Ⅱ)(理科学生作)若A=2C,试求角B的值.
(文科学生作)若A+C=90°，试求角C的值.
17．（本小题满分16分）
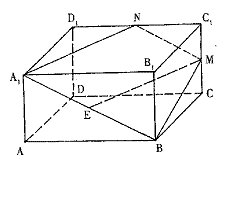
如图，在正四棱柱ABCD—A1B1C1D1中，
，点E，M分别为A1B，C1C的中点，过点A1，B，M三点的平面A1BMN交C1D1于点N.
(Ⅰ)求证:EM//平面A1B1C1D1;
(Ⅱ)求二面角B—A1N—B1的正切值；
(Ⅲ)（理科学生作）设截面A1BMN把该正四棱柱截成的两个几何体的体积分别为V1，V2（V1<V2）,求V1：V2的值.
（文科学生作）设A1A=1，求棱台MNC1—BA1B1的体积V.
18．（本小题满分12分）
用分期付款的方式购买一批总价为2300万元的住房，购买当天首付300万元，以后每月的这一天都交100万元，并加付此前欠款的利息，设月利率为1%，若首付300万元之后的第一个月开始算分期付款的第一个月，问分期付款的第10个月应付多少万元？全部贷款付清后，买这批房实际支付多少万元？
19．（本小题满分16分）
已知曲线C的方程为：
(Ⅰ)若曲线C是椭圆，求k的取值范围；
(Ⅱ)若曲线C的双曲线，且有一条渐近线的倾斜角是60°，求此双曲线的方程；
(Ⅲ)（理科学生作，文科学生不作）满足（Ⅱ）的双曲线上是否存在两点P，Q关于直线l:y=x-1对称，若存在，求出过P，Q的直线方程；若不存在，说明理由.
20．（本小题满分14分）
已知函数f
(x) 是定义在R上的偶函数，当
(Ⅰ)求x<0时，f (x)的解析式；
(Ⅱ)试确定函数y= f (x)(x≥0)的单调区间，并证明你的结论；
(Ⅲ)（理科学生作，文科学生不作）若
证明：