11 导数
一、选择题
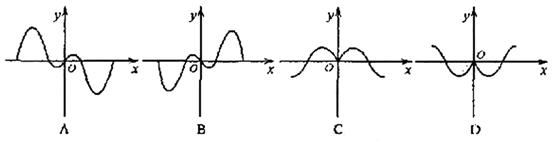
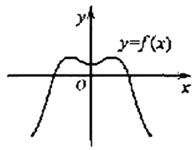
1.(福建11)如果函数y=f(x)的图象如右图,那么
导函数![]() 的图象可能是( A )
的图象可能是( A )
2.(辽宁6)设P为曲线C:![]() 上的点,且曲线C在点P处切线倾斜角的取值范围为
上的点,且曲线C在点P处切线倾斜角的取值范围为![]() ,则点P横坐标的取值范围为( A
)
,则点P横坐标的取值范围为( A
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.(全国Ⅰ4)曲线![]() 在点
在点![]() 处的切线的倾斜角为( B )
处的切线的倾斜角为( B )
A.30° B.45° C.60° D.120°
4.(全国Ⅱ7)设曲线![]() 在点(1,
在点(1,![]() )处的切线与直线
)处的切线与直线![]() 平行,则
平行,则![]() ( A )
( A )
A.1 B.![]() C.
C.![]() D.
D.![]()
二、填空题
1.(北京13)如图,函数![]() 的图象是折线段
的图象是折线段![]() ,其中
,其中![]() 的坐标分别为
的坐标分别为![]() ,则
,则![]() _________;2
_________;2
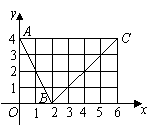 函数
函数![]() 在
在![]() 处的导数
处的导数![]() _________.
_________.![]()
2.(江苏14)![]() 对于
对于![]() 总有
总有![]() 成立,则
成立,则![]() =
4
=
4
三、解答题
1.(安徽20)(本小题满分12分)
设函数![]() 为实数。
为实数。
(Ⅰ)已知函数![]() 在
在![]() 处取得极值,求
处取得极值,求![]() 的值;
的值;
(Ⅱ)已知不等式![]() 对任意
对任意![]() 都成立,求实数
都成立,求实数![]() 的取值范围。
的取值范围。
解: (1)
![]() ,由于函数
,由于函数![]() 在
在![]() 时取得极值,所以
时取得极值,所以 ![]()
即 ![]()
(2) 方法一
由题设知:![]() 对任意
对任意![]() 都成立
都成立
即![]() 对任意
对任意![]() 都成立
都成立
设 ![]() , 则对任意
, 则对任意![]() ,
,![]() 为单调递增函数
为单调递增函数![]()
所以对任意![]() ,
,![]() 恒成立的充分必要条件是
恒成立的充分必要条件是![]()
即 ![]() ,
,![]()
于是![]() 的取值范围是
的取值范围是![]()
方法二
由题设知:![]() 对任意
对任意![]() 都成立
都成立
即![]() 对任意
对任意![]() 都成立
都成立
于是![]() 对任意
对任意![]() 都成立,即
都成立,即![]()
![]()
于是![]() 的取值范围是
的取值范围是![]()
2.(北京17)(本小题共13分)
已知函数![]() ,且
,且![]() 是奇函数.
是奇函数.
(Ⅰ)求![]() ,
,![]() 的值;
的值;
(Ⅱ)求函数![]() 的单调区间.
的单调区间.
解:(Ⅰ)因为函数![]() 为奇函数,
为奇函数,
所以,对任意的![]() ,
,![]() ,即
,即![]() .
.
又![]()
所以![]() .
.
所以![]()
解得![]() .
.
(Ⅱ)由(Ⅰ)得![]() .
.
所以![]() .
.
当![]() 时,由
时,由![]() 得
得![]() .
.
![]() 变化时,
变化时,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
| 0 |
| 0 |
|
所以,当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增.
上单调递增.
3.(福建21)(本小题满分12分)
已知函数![]() 的图象过点(-1,-6),且函数
的图象过点(-1,-6),且函数![]() 的图象关于y轴对称.
的图象关于y轴对称.
(Ⅰ)求m、n的值及函数y=f(x)的单调区间;
(Ⅱ)若a>0,求函数y=f(x)在区间(a-1,a+1)内的极值.
解:(1)由函数f(x)图象过点(-1,-6),得m-n=-3, ……①
由f(x)=x3+mx2+nx-2,得f′(x)=3x2+2mx+n,
则g(x)=f′(x)+6x=3x2+(2m+6)x+n;
而g(x)图象关于y轴对称,所以-![]() =0,所以m=-3,
=0,所以m=-3,
代入①得n=0.
于是f′(x)=3x2-6x=3x(x-2).
由f′(x)>得x>2或x<0,
故f(x)的单调递增区间是(-∞,0),(2,+∞);
由f′(x)<0得0<x<2,
故f(x)的单调递减区间是(0,2).
(Ⅱ)由(Ⅰ)得f′(x)=3x(x-2),
令f′(x)=0得x=0或x=2.
当x变化时,f′(x)、f(x)的变化情况如下表:
| X | (-∞.0) | 0 | (0,2) | 2 | (2,+ ∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) |
| 极大值 | 极小值 |
由此可得:
当0<a<1时,f(x)在(a-1,a+1)内有极大值f(O)=-2,无极小值;
当a=1时,f(x)在(a-1,a+1)内无极值;
当1<a<3时,f(x)在(a-1,a+1)内有极小值f(2)=-6,无极大值;
当a≥3时,f(x)在(a-1,a+1)内无极值.
综上得:当0<a<1时,f(x)有极大值-2,无极小值,当1<a<3时,f(x)有极小值-6,无极大值;当a=1或a≥3时,f(x)无极值.
4.(宁夏21)(本小题满分12分)
设函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)证明:曲线![]() 上任一点处的切线与直线
上任一点处的切线与直线![]() 和直线
和直线![]() 所围成的三角形面积为定值,并求此定值.
所围成的三角形面积为定值,并求此定值.
21.解:
(Ⅰ)方程![]() 可化为
可化为![]() .
.
当![]() 时,
时,![]() .···································································································· 2分
.···································································································· 2分
又![]() ,
,
于是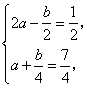 解得
解得![]()
故![]() .········································································································· 6分
.········································································································· 6分
(Ⅱ)设![]() 为曲线上任一点,由
为曲线上任一点,由![]() 知曲线在点
知曲线在点![]() 处的切线方程为
处的切线方程为
 ,
,
即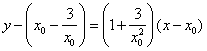 .
.
令![]() 得
得![]() ,从而得切线与直线
,从而得切线与直线![]() 的交点坐标为
的交点坐标为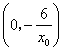 .
.
令![]() 得
得![]() ,从而得切线与直线
,从而得切线与直线![]() 的交点坐标为
的交点坐标为![]() .·············· 10分
.·············· 10分
所以点![]() 处的切线与直线
处的切线与直线![]() ,
,![]() 所围成的三角形面积为
所围成的三角形面积为
![]() .
.
故曲线![]() 上任一点处的切线与直线
上任一点处的切线与直线![]() ,
,![]() 所围成的三角形的面积为定值,此定值为
所围成的三角形的面积为定值,此定值为![]() . 12分
. 12分
5.(江西21)已知函数![]()
(1)求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 的图像与直线
的图像与直线![]() 恰有两个交点,求
恰有两个交点,求![]() 的取值范围.
的取值范围.
解:(1)因为![]()
令![]() 得
得![]()
由![]() 时,
时,![]() 在
在![]() 根的左右的符号如下表所示
根的左右的符号如下表所示
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极小值 |
| 极大值 |
| 极小值 |
|
所以![]() 的递增区间为
的递增区间为![]()
![]() 的递减区间为
的递减区间为![]()
(2)由(1)得到![]() ,
,![]()
![]()
要使![]() 的图像与直线
的图像与直线![]() 恰有两个交点,只要
恰有两个交点,只要![]() 或
或![]() ,
,
即![]() 或
或![]() .
.
6.(湖南21)已知函数![]() 有三个极值点。
有三个极值点。
(I)证明:![]() ;
;
(II)若存在实数c,使函数![]() 在区间
在区间![]() 上单调递减,求
上单调递减,求![]() 的取值范围。
的取值范围。
解:(I)因为函数![]() 有三个极值点,
有三个极值点,
所以![]() 有三个互异的实根.
有三个互异的实根.
设![]() 则
则![]()
当![]() 时,
时,![]()
![]() 在
在![]() 上为增函数;
上为增函数;
当![]() 时,
时,![]()
![]() 在
在![]() 上为减函数;
上为减函数;
当![]() 时,
时,![]()
![]() 在
在![]() 上为增函数;
上为增函数;
所以函数![]() 在
在![]() 时取极大值,在
时取极大值,在![]() 时取极小值.
时取极小值.
当![]() 或
或![]() 时,
时,![]() 最多只有两个不同实根.
最多只有两个不同实根.
因为![]() 有三个不同实根, 所以
有三个不同实根, 所以![]() 且
且![]() .
.
即![]() ,且
,且![]() ,
,
解得![]() 且
且![]() 故
故![]() .
.
(II)由(I)的证明可知,当![]() 时,
时, ![]() 有三个极值点.
有三个极值点.
不妨设为![]() (
(![]() ),则
),则![]()
所以![]() 的单调递减区间是
的单调递减区间是![]() ,
,![]()
若![]() 在区间
在区间![]() 上单调递减,
上单调递减,
则![]()
![]() , 或
, 或![]()
![]() ,
,
若![]()
![]() ,则
,则![]() .由(I)知,
.由(I)知,![]() ,于是
,于是![]()
若![]()
![]() ,则
,则![]() 且
且![]() .由(I)知,
.由(I)知,![]()
又![]() 当
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
因此, 当![]() 时,
时,![]() 所以
所以![]() 且
且![]()
即![]() 故
故![]() 或
或![]() 反之, 当
反之, 当![]() 或
或![]() 时,
时,
总可找到![]() 使函数
使函数![]() 在区间
在区间![]() 上单调递减.
上单调递减.
综上所述, ![]() 的取值范围是
的取值范围是![]() .
.
7.(辽宁22)(本小题满分14分)
设函数![]() 在
在![]() ,
,![]() 处取得极值,且
处取得极值,且![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的值,并求
的值,并求![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() ,求
,求![]() 的取值范围.
的取值范围.
解:![]() .①················································································ 2分
.①················································································ 2分
(Ⅰ)当![]() 时,
时,
![]() ;
;
由题意知![]() 为方程
为方程![]() 的两根,所以
的两根,所以
![]() .
.
由![]() ,得
,得![]() .··························································································· 4分
.··························································································· 4分
从而![]() ,
,![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
故![]() 在
在![]() 单调递减,在
单调递减,在![]() ,
,![]() 单调递增.···································· 6分
单调递增.···································· 6分
(Ⅱ)由①式及题意知![]() 为方程
为方程![]() 的两根,
的两根,
所以![]() .
.
从而![]() ,
,
由上式及题设知![]() .························································································· 8分
.························································································· 8分
考虑![]() ,
,
![]() .········································································ 10分
.········································································ 10分
故![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,从而
单调递减,从而![]() 在
在![]() 的极大值为
的极大值为![]() .
.
又![]() 在
在![]() 上只有一个极值,所以
上只有一个极值,所以![]() 为
为![]() 在
在![]() 上的最大值,且最小值为
上的最大值,且最小值为![]() .
.
所以![]() ,即
,即![]() 的取值范围为
的取值范围为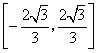 .··············································· 14分
.··············································· 14分
8.(全国Ⅰ21)(本小题满分12分)
已知函数![]() ,
,![]() .
.
(Ⅰ)讨论函数![]() 的单调区间;
的单调区间;
(Ⅱ)设函数![]() 在区间
在区间![]() 内是减函数,求
内是减函数,求![]() 的取值范围.
的取值范围.
解:(1)![]()
求导:![]()
当![]() 时,
时,![]() ,
,![]()
![]() 在
在![]() 上递增
上递增
当![]() ,
,![]() 求得两根为
求得两根为![]()
即![]() 在
在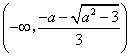 递增,
递增,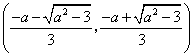 递减,
递减,
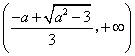 递增
递增
(2)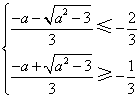 ,且
,且![]()
解得:![]()
9.(全国Ⅱ21)(本小题满分12分)
设![]() ,函数
,函数![]() .
.
(Ⅰ)若![]() 是函数
是函数![]() 的极值点,求
的极值点,求![]() 的值;
的值;
(Ⅱ)若函数![]() ,在
,在![]() 处取得最大值,求
处取得最大值,求![]() 的取值范围.
的取值范围.
解:(Ⅰ)![]() .
.
因为![]() 是函数
是函数![]() 的极值点,所以
的极值点,所以![]() ,即
,即![]() ,因此
,因此![]() .
.
经验证,当![]() 时,
时,![]() 是函数
是函数![]() 的极值点.··············································· 4分
的极值点.··············································· 4分
(Ⅱ)由题设,![]() .
.
当![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() 时,
时,
![]() ,
,
即![]() .
.
故得![]() .··············································································································· 9分
.··············································································································· 9分
反之,当![]() 时,对任意
时,对任意![]() ,
,
![]()
![]()
![]()
![]() ,
,
而![]() ,故
,故![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() .
.
综上,![]() 的取值范围为
的取值范围为![]() . 12分
. 12分
10.(山东21)(本小题满分12分)
设函数![]() ,已知
,已知![]() 和
和![]() 为
为![]() 的极值点.
的极值点.
(Ⅰ)求![]() 和
和![]() 的值;
的值;
(Ⅱ)讨论![]() 的单调性;
的单调性;
(Ⅲ)设![]() ,试比较
,试比较![]() 与
与![]() 的大小.
的大小.
解:(Ⅰ)因为![]()
![]() ,
,
又![]() 和
和![]() 为
为![]() 的极值点,所以
的极值点,所以![]() ,
,
因此![]()
解方程组得![]() ,
,![]() .
.
(Ⅱ)因为![]() ,
,![]() ,
,
所以![]() ,
,
令![]() ,解得
,解得![]() ,
,![]() ,
,![]() .
.
因为当![]()
![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
所以![]() 在
在![]() 和
和![]() 上是单调递增的;
上是单调递增的;
在![]() 和
和![]() 上是单调递减的.
上是单调递减的.
(Ⅲ)由(Ⅰ)可知![]() ,
,
故![]() ,
,
令![]() ,
,
则![]() .
.
令![]() ,得
,得![]() ,
,
因为![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递减.
上单调递减.
故![]() 时,
时,![]() ;
;
因为![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递增.
上单调递增.
故![]() 时,
时,![]() .
.
所以对任意![]() ,恒有
,恒有![]() ,又
,又![]() ,
,
因此![]() ,
,
故对任意![]() ,恒有
,恒有![]() .
.
11.(四川20)(本小题满分12分)
设![]() 和
和![]() 是函数
是函数![]() 的两个极值点。
的两个极值点。
(Ⅰ)求![]() 和
和![]() 的值;
的值;
(Ⅱ)求![]() 的单调区间
的单调区间
【解】:(Ⅰ)因为![]()
由假设知:![]()
![]()
解得![]()
(Ⅱ)由(Ⅰ)知
![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
因此![]() 的单调增区间是
的单调增区间是![]()
![]() 的单调减区间是
的单调减区间是![]()
12.(天津21)(本小题满分14分)
设函数![]() ,其中
,其中![]() .
.
(Ⅰ)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(Ⅱ)若函数![]() 仅在
仅在![]() 处有极值,求
处有极值,求![]() 的取值范围;
的取值范围;
(Ⅲ)若对于任意的![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围.
的取值范围.
(Ⅰ)解:![]() .
.
当![]() 时,
时,
![]() .
.
令![]() ,解得
,解得![]() ,
,![]() ,
,![]() .
.
当![]() 变化时,
变化时,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ↘ | 极小值 | ↗ | 极大值 | ↘ | 极小值 | ↗ |
所以![]() 在
在![]() ,
,![]() 内是增函数,在
内是增函数,在![]() ,
,![]() 内是减函数.
内是减函数.
(Ⅱ)解:![]() ,显然
,显然![]() 不是方程
不是方程![]() 的根.
的根.
为使![]() 仅在
仅在![]() 处有极值,必须
处有极值,必须![]() 恒成立,即有
恒成立,即有![]() .
.
解此不等式,得![]() .这时,
.这时,![]() 是唯一极值.
是唯一极值.
因此满足条件的![]() 的取值范围是
的取值范围是![]() .
.
(Ⅲ)解:由条件![]() 可知
可知![]() ,从而
,从而![]() 恒成立.
恒成立.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
因此函数![]() 在
在![]() 上的最大值是
上的最大值是![]() 与
与![]() 两者中的较大者.
两者中的较大者.
为使对任意的![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,当且仅当
上恒成立,当且仅当
![]() 即
即![]()
在![]() 上恒成立.
上恒成立.
所以![]() ,因此满足条件的
,因此满足条件的![]() 的取值范围是
的取值范围是![]() .
.
13.(浙江21)(本题15分)已知![]() 是实数,函数
是实数,函数![]() 。
。
(Ⅰ)若![]() ,求
,求![]() 的值及曲线
的值及曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)求![]() 在区间
在区间![]() 上的最大值。
上的最大值。
(Ⅰ)解:![]() ,
,
因为![]() ,
,
所以![]() .
.
又当![]() 时,
时,![]() ,
,![]() ,
,
所以曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅱ)解:令![]() ,解得
,解得![]() ,
,![]() .
.
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递增,从而
上单调递增,从而
![]() .
.
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递减,从而
上单调递减,从而
![]() .
.
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,从而
上单调递增,从而![]()
综上所述, ![]()
14.(重庆19)(本小题满分12分,(Ⅰ)小问6分,(Ⅱ)小问6分.)
设函数![]() 若曲线y=f(x)的斜率最小的切线与直线12x+y=6平行,求:
若曲线y=f(x)的斜率最小的切线与直线12x+y=6平行,求:
(Ⅰ)a的值;
(Ⅱ)函数f(x)的单调区间.
解:(Ⅰ)因![]()
所以![]()
![]()
即当![]()
因斜率最小的切线与![]() 平行,即该切线的斜率为-12,
平行,即该切线的斜率为-12,
所以![]()
解得![]()
(Ⅱ)由(Ⅰ)知![]()

15.(湖北17).(本小题满分12分)
已知函数![]() (m为常数,且m>0)有极大值9.
(m为常数,且m>0)有极大值9.
(Ⅰ)求m的值;
(Ⅱ)若斜率为-5的直线是曲线![]() 的切线,求此直线方程.
的切线,求此直线方程.
解:(Ⅰ) f’(x)=3x2+2mx-m2=(x+m)(3x-m)=0,则x=-m或x=![]() m,
m,
当x变化时,f’(x)与f(x)的变化情况如下表:
| x | (-∞,-m) | -m | (-m, |
| ( |
| f’(x) |
| 0 | - | 0 | + |
| f (x) | 极大值 | 极小值 |
从而可知,当x=-m时,函数f(x)取得极大值9,
即f(-m)=-m3+m3+m3+1=9,∴m=2.
(Ⅱ)由(Ⅰ)知,f(x)=x3+2x2-4x+1,
依题意知f’(x)=3x2+4x-4=-5,∴x=-1或x=-![]() .
.
又f(-1)=6,f(-![]() )=
)=![]() ,
,
所以切线方程为y-6=-5(x+1),或y-![]() =-5(x+
=-5(x+![]() ),
),
即5x+y-1=0,或135x+27y-23=0.
16.(陕西22) 本小题满分14分)
设函数![]() 其中实数
其中实数![]() .
.
(Ⅰ)若![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)当函数![]() 与
与![]() 的图象只有一个公共点且
的图象只有一个公共点且![]() 存在最小值时,记
存在最小值时,记![]() 的最小值为
的最小值为![]() ,求
,求![]() 的值域;
的值域;
(Ⅲ)若![]() 与
与![]() 在区间
在区间![]() 内均为增函数,求
内均为增函数,求![]() 的取值范围.
的取值范围.
解:(Ⅰ)![]()
![]() ,又
,又![]() ,
,
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
![]()
![]() 在
在![]() 和
和![]() 内是增函数,在
内是增函数,在![]() 内是减函数.
内是减函数.
(Ⅱ)由题意知
![]() ,
,
即![]() 恰有一根(含重根).
恰有一根(含重根).![]()
![]() ≤
≤![]() ,即
,即![]() ≤
≤![]() ≤
≤![]() ,
,
又![]() ,
,![]()
![]() .
.
当![]() 时,
时,![]() 才存在最小值,
才存在最小值,![]()
![]() .
.![]()
![]() ,
,
![]()
![]() .
. ![]()
![]() 的值域为
的值域为![]() .
.
(Ⅲ)当![]() 时,
时,![]() 在
在![]() 和
和![]() 内是增函数,
内是增函数,![]() 在
在![]() 内是增函数.
内是增函数.
由题意得![]() ,解得
,解得![]() ≥
≥![]() ;
;
当![]() 时,
时,![]() 在
在![]() 和
和![]() 内是增函数,
内是增函数,![]() 在
在![]() 内是增函数.
内是增函数.
由题意得 ,解得
,解得![]() ≤
≤![]() ;
;
综上可知,实数![]() 的取值范围为
的取值范围为![]() .
.