04 三角与向量
一、选择题
1.(安徽2).若![]() ,
,![]() , 则
, 则![]() ( B )
( B )
A. (1,1) B.(-1,-1) C.(3,7) D.(-3,-7)
2.(安徽5).在三角形![]() 中,
中,![]() ,则
,则![]() 的大小为( A )
的大小为( A )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.(安徽8).函数![]() 图像的对称轴方程可能是( D )
图像的对称轴方程可能是( D )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.(北京4)已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,那么角
,那么角![]() 等于( C )
等于( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.(福建7)函数y=cosx(x∈R)的图象向左平移![]() 个单位后,得到函数y=g(x)的图象,则g(x)的解析式为( A )
个单位后,得到函数y=g(x)的图象,则g(x)的解析式为( A )
A.-sinx B.sinx C.-cosx D.cosx
6.(福建8)在△ABC中,角A、B、C的对边分别为a、b、c,若a2+c2-b2![]() ac,则角B的值为( A )
ac,则角B的值为( A )
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
7.(广东3)已知平面向量a=(1,2), b=(-2,m), 且a∥b, 则2a+3b= ( B )
A.(-2,-4) B.(-3,-6) C.(-4,-8) D.(-5,-10)
8.(广东5)已知函数f(x)=(1+cos2x)sin3x,x∈R, 则f(x)是 ( D )
A.最小正周期为![]() 的奇函数 B.最小正周期为
的奇函数 B.最小正周期为![]() 的偶函数
的偶函数
C.最小正周期为![]() 的奇函数 D.最小正周期为
的奇函数 D.最小正周期为![]() 的偶函数
的偶函数
9.(宁夏5)已知平面向量![]() ,
,![]() ,
,![]() 与
与![]() 垂直,
垂直,
则![]() ( A )
( A )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.(宁夏9)平面向量a,b共线的充要条件是( D )
A.a,b方向相同
B.a,b两向量中至少有一个为零向量
C.![]() ,
,![]()
D.存在不全为零的实数![]() ,
,![]() ,
,![]()
11.(宁夏11)函数![]() 的最小值和最大值分别为( C )
的最小值和最大值分别为( C )
A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]()
12.(湖南7)在![]() 中,AB=3,AC=2,BC=
中,AB=3,AC=2,BC=![]() ,则
,则![]() ( D )
( D )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
13.(江西6)函数 是(
A )
是(
A )
A.以![]() 为周期的偶函数
B.以
为周期的偶函数
B.以![]() 为周期的奇函数
为周期的奇函数
C.以![]() 为周期的偶函数
D.以
为周期的偶函数
D.以![]() 为周期的奇函数
为周期的奇函数
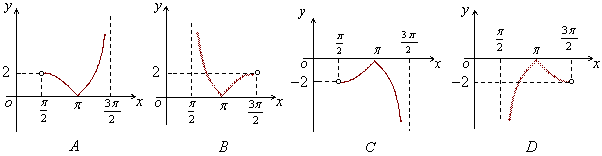
14.(江西10)函数![]() 在区间
在区间![]() 内的图象是( D )
内的图象是( D )
 15.(辽宁5)已知四边形
15.(辽宁5)已知四边形![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() ,且
,且![]() ,则顶点
,则顶点![]() 的坐标为( A )
的坐标为( A )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
16.(辽宁8)将函数![]() 的图象按向量
的图象按向量![]() 平移得到函数
平移得到函数![]() 的图象,则( A )
的图象,则( A )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
17.(全国Ⅰ5) 在![]() 中,
中,![]() ,
,![]() .若点
.若点![]() 满足
满足![]() ,则
,则![]() =( A )
=( A )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
18.(全国Ⅰ6)![]() 是( D )
是( D )
A.最小正周期为![]() 的偶函数 B.最小正周期为
的偶函数 B.最小正周期为![]() 的奇函数
的奇函数
C.最小正周期为![]() 的偶函数 D.最小正周期为
的偶函数 D.最小正周期为![]() 的奇函数
的奇函数
19.(全国Ⅰ9)为得到函数![]() 的图象,只需将函数
的图象,只需将函数![]() 的图像( C )
的图像( C )
A.向左平移![]() 个长度单位 B.向右平移
个长度单位 B.向右平移![]() 个长度单位
个长度单位
C.向左平移![]() 个长度单位 D.向右平移
个长度单位 D.向右平移![]() 个长度单位
个长度单位
20.(全国Ⅱ1)若![]() 且
且![]() 是,则
是,则![]() 是( C )
是( C )
A.第一象限角 B. 第二象限角 C. 第三象限角 D. 第四象限角
21.(全国Ⅱ10)函数![]() 的最大值为( B )
的最大值为( B )
A.1 B. ![]() C.
C.![]() D.2
D.2
22.(山东8) 已知![]() 为
为![]() 的三个内角
的三个内角![]() 的对边,向量
的对边,向量![]() .若
.若![]() ,且
,且![]() ,则角
,则角![]() 的大小分别为( C )
的大小分别为( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
23.(山东10) 已知![]() ,则
,则![]() 的值是( C )
的值是( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
24.(四川3)设平面向量![]() ,则
,则![]() ( A )
( A )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
25.(四川4)![]() ( D )
( D )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
26.(四川7)![]() 的三内角
的三内角![]() 的对边边长分别为
的对边边长分别为![]() ,若
,若![]() ,则
,则![]() ( B )
( B )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
27.(天津6) 把函数![]() 的图象上所有的点向左平行移动
的图象上所有的点向左平行移动![]() 个单位长度,再把所得图象上所有点的横坐标缩短到原来的
个单位长度,再把所得图象上所有点的横坐标缩短到原来的![]() 倍(纵坐标不变),得到的图象所表示的函数是( C
)
倍(纵坐标不变),得到的图象所表示的函数是( C
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
28.(天津9) 设![]() ,
,![]() ,
,![]() ,则( D
)
,则( D
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
29.(浙江2)函数![]() 的最小正周期是 ( B
)
的最小正周期是 ( B
)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
30.(浙江7)在同一平面直角坐标系中,函数![]() 的图象和直线
的图象和直线![]() 的交点个数是 ( C )
的交点个数是 ( C )
(A)0 (B)1 (C)2 (D)4
31.(重庆12)函数f(x)=![]() (0≤x≤2
(0≤x≤2![]() )的值域是 ( C
)
)的值域是 ( C
)
(A)[-![]() ] (B)[-
] (B)[-![]() ]
]
(C)[-![]() ] (D)[-
] (D)[-![]() ]
]
32.(湖北1).设![]() ( C )
( C )
A.![]() B.0
C.-3
D.-11
B.0
C.-3
D.-11
33.(湖北7).将函数![]() 的图象F向右平移
的图象F向右平移![]() 个单位长度得到图象F′,若F′的一条对称轴是直线
个单位长度得到图象F′,若F′的一条对称轴是直线![]() 则
则![]() 的一个可能取值是 ( A
)
的一个可能取值是 ( A
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
34.(陕西1) ![]() 等于( B )
等于( B )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题
1.(北京9)若角![]() 的终边经过点
的终边经过点![]() ,则
,则![]() 的值为______________.
的值为______________.![]()
2.(北京11)已知向量![]() 与
与![]() 的夹角为
的夹角为![]() ,且
,且![]() ,那么
,那么![]() 的值为________.
的值为________.![]()
3.(湖南11)已知向量![]() ,
,![]() ,则
,则![]() =_____________________.2
=_____________________.2
4.(江苏1)![]() 最小正周期为
最小正周期为![]() ,其中
,其中![]() ,则
,则![]() 10
10
5.(江苏5)![]() 的夹角为
的夹角为![]() ,
,![]() ,则
,则![]() 7
7
6.(江苏13)若![]() ,则
,则![]() 的最大值
的最大值 ![]()
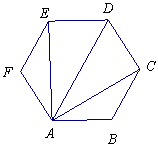
7.(江西16)如图,正六边形![]() 中,有下列四个命题:
中,有下列四个命题:
 A.
A.![]()
B.![]()
C.![]()
D.![]()
其中真命题的代号是
![]() (写出所有真命题的代号).
(写出所有真命题的代号).
8.(辽宁16)设![]() ,则函数
,则函数![]() 的最小值为
.
的最小值为
.![]()
9.(全国Ⅱ13)设向量![]() ,若向量
,若向量![]() 与向量
与向量![]() 共线,则
共线,则![]() .2
.2
10.(上海5)若向量![]() ,
,![]() 满足
满足![]() 且
且![]() 与
与![]() 的夹角为
的夹角为![]() ,则
,则![]() .
.![]()
11.(天津14) 已知平面向量![]() ,
,![]() ,若
,若![]() ,则
,则![]() .
.![]()
12.(浙江12)若![]() ,则
,则![]() _________。
_________。![]()
13.(浙江14)在△ABC中,角A、B、C所对的边分别为![]() 、b、c ,若
、b、c ,若![]() ,则
,则![]() 。
。![]()
14.(浙江16)已知![]() 是平面内的单位向量,若向量
是平面内的单位向量,若向量![]() 满足
满足![]() ,则
,则![]() 的取值范围是
。
的取值范围是
。![]()
15.(湖北12).在△ABC中,a,b,c分别是角A,B,C所对的边,已知![]() 则A=
.
则A=
. ![]()
16.(陕西13) ![]() 的内角
的内角![]() 的对边分别为
的对边分别为![]() ,
,
若![]() ,则
,则![]()
![]() .
.
17.(陕西15) 关于平面向量![]() .有下列三个命题:
.有下列三个命题:
①若![]() ,则
,则![]() .②若
.②若![]() ,
,![]() ,则
,则![]() .
.
③非零向量![]() 和
和![]() 满足
满足![]() ,则
,则![]() 与
与![]() 的夹角为
的夹角为![]() .
.
其中真命题的序号为 ② .(写出所有真命题的序号)
三、解答题
1.(安徽17).(本小题满分12分)
已知函数![]()
(Ⅰ)求函数![]() 的最小正周期和图象的对称轴方程
的最小正周期和图象的对称轴方程
(Ⅱ)求函数![]() 在区间
在区间![]() 上的值域
上的值域
解:(1)![]()
![]()
![]()
![]()
![]()
![]()
(2)![]()
因为![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,
上单调递减,
所以
当![]() 时,
时,![]() 取最大值 1
取最大值 1
又 ![]() ,
,![]() 当
当![]() 时,
时,![]() 取最小值
取最小值![]()
所以 函数 ![]() 在区间
在区间![]() 上的值域为
上的值域为![]()
2.(北京15)(本小题共13分)
已知函数![]() (
(![]() )的最小正周期为
)的最小正周期为![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求函数![]() 在区间
在区间![]() 上的取值范围.
上的取值范围.
解:(Ⅰ)![]()
![]()
![]() .
.
因为函数![]() 的最小正周期为
的最小正周期为![]() ,且
,且![]() ,
,
所以![]() ,解得
,解得![]() .
.
(Ⅱ)由(Ⅰ)得![]() .
.
因为![]() ,
,
所以![]() ,
,
所以![]() .
.
因此![]() ,即
,即![]() 的取值范围为
的取值范围为![]() .
.
3.(福建17)(本小题满分12分)
已知向量![]() ,且
,且![]()
(Ⅰ)求tanA的值;
(Ⅱ)求函数![]() R)的值域.
R)的值域.
解:(Ⅰ)由题意得
m·n=sinA-2cosA=0,
因为cosA≠0,所以tanA=2.
(Ⅱ)由(Ⅰ)知tanA=2得
![]()
因为x![]() R,所以
R,所以![]() .
.
当![]() 时,f(x)有最大值
时,f(x)有最大值![]() ,
,
当sinx=-1时,f(x)有最小值-3,
所以所求函数f(x)的值域是![]()
4.(广东16)(本小题满分13分)
已知函数f(x)=Asin(x+![]() )(A>0,0<
)(A>0,0<![]() <
<![]() ),x
),x![]() R的最大值是1,其图像经过点M
R的最大值是1,其图像经过点M![]() .
.
(1)求f(x)的解析式;
(2)已知α,β![]()
![]() ,且f(α)=
,且f(α)=![]() ,f(β)=
,f(β)=![]() ,求f(α-β)的值.
,求f(α-β)的值.
解:(1)依题意知 A=1
![]() , 又
, 又![]() ;
;
![]()
![]() 即
即
![]()
因此 ![]() ;
;
(2)![]()
![]() ,
,![]()
且 ![]()
![]()
![]() ,
,![]()
![]()
5.(宁夏17)(本小题满分12分)
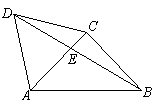 如图,
如图,![]() 是等边三角形,
是等边三角形,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() 交
交![]() 于
于![]() ,
,![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求![]() .
.
解:(Ⅰ)因为![]() ,
,![]() ,
,
所以![]() .
.
所以![]() .···························································· 6分
.···························································· 6分
(Ⅱ)在![]() 中,
中,![]() ,
,
由正弦定理![]() .
.
故![]()
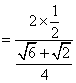
![]() . 12分
. 12分
6.(江苏15)(14分)
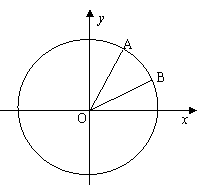 如图,在平面直角坐标系xoy中,以ox轴为始边做两个锐角
如图,在平面直角坐标系xoy中,以ox轴为始边做两个锐角![]() ,它们的终边分别与单位圆相交于A、B两点,已知A、B的横坐标分别为
,它们的终边分别与单位圆相交于A、B两点,已知A、B的横坐标分别为![]()
(1)求![]() 的值; (2)求
的值; (2)求![]() 的值。
的值。
【解析】:本小题考查三角函数的基本概念、三角函数
的基本关系式、两角和的正切、二倍角的正切公式,
考查运算求解能力。
由条件得![]()
![]() 为锐角,
为锐角,![]()
![]()
(1)
(2)

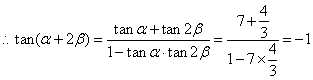
![]() 为锐角,
为锐角,![]()
![]()
7.(江苏17)(14分)
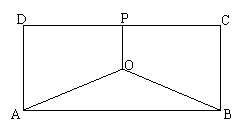
某地有三家工厂,分别位于矩形ABCD的顶点A、B及CD的中点P处,已知AB=20km,BC=10km,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A、B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO、BO、OP,设排污管道的总长为ykm。
(1)按下列要求写出函数关系式:
①设∠BAO=θ(rad),将y表示成θ的函数关系式;
②设OP=x(km),将y表示成x的函数关系式;
 (2)请你选用(1)中的一个函数关系式,确定污水处理厂的位置,使三条排污管道总长度最短。
(2)请你选用(1)中的一个函数关系式,确定污水处理厂的位置,使三条排污管道总长度最短。
【解析】:本小题考查函数的概念、
解三角形、导数等基本知识,考查数学建模能力、
抽象概括能力和解决实际问题的能力。
(1)①由条件知PQ垂直平分AB,若∠BAO=θ(rad),则![]() ,
,
故![]()
又![]() ,所以
,所以![]()
所求函数关系式为![]()
②若OP=x(km),则OQ=10-x,所以![]()
所求函数关系式为![]()
(2)选择函数模型①,![]()
令![]() 得
得![]()
![]()
当![]() 时
时![]() ,y是θ的减函数;当
,y是θ的减函数;当![]() 时
时![]() ,y是θ的增函数;
,y是θ的增函数;
所以当![]() 时,
时,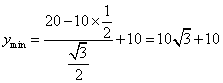
此时点O位于线段AB的中垂线上,且距离AB边![]() km处。
km处。
8.(江西17)已知![]() ,
,![]()
![]()
(1)求![]() 的值;
的值;
(2)求函数![]() 的最大值.
的最大值.
解:(1)由![]()
![]()
得![]() ,
,![]()
于是![]() =
=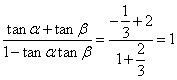 .
.
(2)因为![]()
所以![]()
![]()
![]()
![]() 的最大值为
的最大值为![]() .
.
9.(湖南17)(本小题满分12分)
已知函数f(x)=cox2![]()
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)当x0∈(0,![]() )且f(x0)=
)且f(x0)=![]() 时,求f(x0+
时,求f(x0+![]() )的值.
)的值.
解 由题设有f(x)=cosx+sinx=![]() .
.
(Ⅰ)函数f(x)的最小正周期是T=2x.
(Ⅱ)由f(x0)=![]() 得
得![]() ,即sin
,即sin![]()
因为x0∈(0,![]() ),所以
),所以![]()
从而cos![]() .
.
于是![]()
![]()
![]()
10.(辽宁17)(本小题满分12分)
在![]() 中,内角
中,内角![]() 对边的边长分别是
对边的边长分别是![]() ,已知
,已知![]() ,
,![]() .
.
(Ⅰ)若![]() 的面积等于
的面积等于![]() ,求
,求![]() ;
;
(Ⅱ)若![]() ,求
,求![]() 的面积.
的面积.
解:(Ⅰ)由余弦定理得,![]() ,
,
又因为![]() 的面积等于
的面积等于![]() ,所以
,所以![]() ,得
,得![]() .···························· 4分
.···························· 4分
联立方程组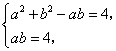 解得
解得![]() ,
,![]() .······················································ 6分
.······················································ 6分
(Ⅱ)由正弦定理,已知条件化为![]() ,·································································· 8分
,·································································· 8分
联立方程组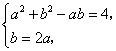 解得
解得![]() ,
,![]() .
.
所以![]() 的面积
的面积![]() .······························································ 12分
.······························································ 12分
11.(全国Ⅰ17)(本小题满分12分)
设![]() 的内角
的内角![]() 所对的边长分别为
所对的边长分别为![]() ,且
,且![]() ,
,![]() .
.
(Ⅰ)求边长![]() ;
;
(Ⅱ)若![]() 的面积
的面积![]() ,求
,求![]() 的周长
的周长![]() .
.
解:(1)由![]() 与
与![]() 两式相除,有:
两式相除,有:
![]()
又通过![]() 知:
知:![]() ,
,
则![]() ,
,![]() ,
,
则![]() .
.
(2)由![]() ,得到
,得到![]() .
.
由![]() ,
,
解得:![]() ,
,
最后![]() .
.
12.(全国Ⅱ17)(本小题满分10分)
在![]() 中,
中,![]() ,
,![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)设![]() ,求
,求![]() 的面积.
的面积.
解:(Ⅰ)由![]() ,得
,得![]() ,
,
由![]() ,得
,得![]() .······················································································· 2分
.······················································································· 2分
所以![]() .··········································· 5分
.··········································· 5分
(Ⅱ)由正弦定理得 .·················································· 8分
.·················································· 8分
所以![]() 的面积
的面积![]()
![]()
![]() .························· 10分
.························· 10分
13.(山东17)(本小题满分12分)
已知函数![]() (
(![]() ,
,![]() )为偶函数,且函数
)为偶函数,且函数![]() 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后,得到函数
个单位后,得到函数![]() 的图象,求
的图象,求![]() 的单调递减区间.
的单调递减区间.
解:(Ⅰ)![]()
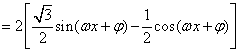
![]() .
.
因为![]() 为偶函数,
为偶函数,
所以对![]() ,
,![]() 恒成立,
恒成立,
因此![]() .
.
即![]() ,
,
整理得![]() .
.
因为![]() ,且
,且![]() ,
,
所以![]() .
.
又因为![]() ,
,
故![]() .
.
所以![]() .
.
由题意得![]() ,所以
,所以![]() .
.
故![]() .
.
因此![]() .
.
(Ⅱ)将![]() 的图象向右平移
的图象向右平移![]() 个单位后,得到
个单位后,得到![]() 的图象,
的图象,
所以![]() .
.
当![]() (
(![]() ),
),
即![]() (
(![]() )时,
)时,![]() 单调递减,
单调递减,
因此![]() 的单调递减区间为
的单调递减区间为![]() (
(![]() ).
).
14.(上海17)(本题满分13分)
如图,某住宅小区的平面图呈扇形AOC.小区的两个出入口设置在点A及点C处,小区里
有两条笔直的小路![]() ,且拐弯处的转角为
,且拐弯处的转角为![]() .已知某人从
.已知某人从![]() 沿
沿![]() 走到
走到![]() 用了10分钟,从
用了10分钟,从![]() 沿
沿![]() 走到
走到![]() 用了6分钟.若此人步行的速度为每分钟50米,求该扇形的半径
用了6分钟.若此人步行的速度为每分钟50米,求该扇形的半径![]() 的长(精确到1米).
的长(精确到1米).
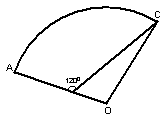 |
【解法一】设该扇形的半径为r米. 由题意,得
CD=500(米),DA=300(米),∠CDO=![]() ……………………………4分
……………………………4分
在![]() 中,
中,![]() ……………6分
……………6分
即![]() …………………….9分
…………………….9分
解得![]() (米). …………………………………………….13分
(米). …………………………………………….13分
【解法二】连接AC,作OH⊥AC,交AC于H…………………..2分
由题意,得CD=500(米),AD=300(米),![]() ………….4分
………….4分

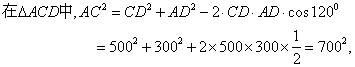
∴ AC=700(米) …………………………..6分
![]() ………….…….9分
………….…….9分
在直角![]()
∴ ![]() (米). ………………………13分
(米). ………………………13分
15.(上海18)(本题满分15分)本题共有2个小题,第1个题满分5分,第2小题满分10分.
已知函数f(x)=sin2x,g(x)=cos![]() ,直线
,直线![]() 与函数
与函数![]() 的图像分别交于M、N两点.
的图像分别交于M、N两点.
(1)当![]() 时,求|MN|的值;
时,求|MN|的值;
(2)求|MN|在![]() 时的最大值.
时的最大值.
【解】(1)![]() …………….2分
…………….2分
![]() ………………………………5分
………………………………5分
(2)![]()
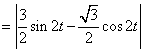 …………...8分
…………...8分
![]() …………………………….11分
…………………………….11分
∵ ![]() …………13分
…………13分
∴ |MN|的最大值为![]() .
……………15分
.
……………15分
16.(四川17)(本小题满分12分)
求函数![]() 的最大值与最小值。
的最大值与最小值。
【解】:![]()
![]()
![]()
![]()
![]()
由于函数![]() 在
在![]() 中的最大值为
中的最大值为
![]()
最小值为
![]()
故当![]() 时
时![]() 取得最大值
取得最大值![]() ,当
,当![]() 时
时![]() 取得最小值
取得最小值![]()
17.(天津17)(本小题满分12分)
已知函数![]() 的最小正周期是
的最小正周期是![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求函数![]() 的最大值,并且求使
的最大值,并且求使![]() 取得最大值的
取得最大值的![]() 的集合.
的集合.
(Ⅰ)解:![]()
![]()
![]()
![]() .
.
由题设,函数![]() 的最小正周期是
的最小正周期是![]() ,可得
,可得![]() ,所以
,所以![]() .
.
(Ⅱ)解:由(Ⅰ)知,![]() .
.
当![]() ,即
,即![]() 时,
时,![]() 取得最大值1,所以函数
取得最大值1,所以函数![]() 的最大值是
的最大值是![]() ,此时
,此时![]() 的集合为
的集合为![]() .
.
18.(重庆17)(本小题满13分,(Ⅰ)小问5分,(Ⅱ)小问8分.)
设△ABC的内角A,B,C的对边分别为a,b,c.已知![]() ,求:
,求:
(Ⅰ)A的大小;
(Ⅱ)![]() 的值.
的值.
解:(Ⅰ)由余弦定理,![]()
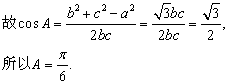
(Ⅱ) ![]()

19.(湖北16).(本小题满12分)
已知函数![]()
(Ⅰ)将函数![]() 化简成
化简成![]() 的形式,并指出
的形式,并指出![]() 的周期;
的周期;
(Ⅱ)求函数![]() 上的最大值和最小值
上的最大值和最小值
解:(Ⅰ)f(x)=![]() sinx+
sinx+![]() .
.
故f(x)的周期为2kπ{k∈Z且k≠0}.
(Ⅱ)由π≤x≤![]() π,得
π,得![]() .因为f(x)=
.因为f(x)=![]() 在[
在[![]() ]上是减函数,在[
]上是减函数,在[![]() ]上是增函数.
]上是增函数.
故当x=![]() 时,f(x)有最小值-
时,f(x)有最小值-![]() ;而f(π)=-2,f(
;而f(π)=-2,f(![]() π)=-
π)=-![]() <-2,
<-2,
所以当x=π时,f(x)有最大值-2.
20.(陕西17)(本小题满分12分)
已知函数![]() .
.
(Ⅰ)求函数![]() 的最小正周期及最值;
的最小正周期及最值;
(Ⅱ)令![]() ,判断函数
,判断函数![]() 的奇偶性,并说明理由.
的奇偶性,并说明理由.
解:(Ⅰ)![]()
![]()
![]() .
.
![]() 的最小正周期
的最小正周期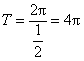 .
.
当![]() 时,
时,![]() 取得最小值
取得最小值![]() ;当
;当![]() 时,
时,![]() 取得最大值2.
取得最大值2.
(Ⅱ)由(Ⅰ)知![]() .又
.又![]() .
.
![]()
![]()
![]()
![]() .
.
![]()
![]() .
.
![]() 函数
函数![]() 是偶函数.
是偶函数.