02 函数
一、选择题
1.(安徽6).函数![]() 的反函数为 ( C )
的反函数为 ( C )
A.![]() B.
B.
![]()
C.![]() D.
D. ![]()
2.(安徽9).设函数![]() 则
则![]() ( A )
( A )
A.有最大值 B.有最小值 C.是增函数 D.是减函数
3.(北京2)若![]() ,则( A )
,则( A )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.(北京5)函数![]() 的反函数为( B )
的反函数为( B )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.(福建4)函数f(x)=x3+sinx+1(x∈R),若f(a)=2, 则f(-a)的值为( B )
A.3 B.0 C.-1 D.-2
6.(湖南4)函数![]() 的反函数是 ( B )
的反函数是 ( B )
![]()
![]()
![]()
![]()
7.(湖南6)下面不等式成立的是 ( A )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.(江西3)若函数![]() 的定义域是
的定义域是![]() ,则函数
,则函数![]() 的定义域是( B )
的定义域是( B )
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
9.(江西4)若![]() ,则( C
)
,则( C
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.(江西12)已知函数![]() ,
,![]() ,若对于任一实数
,若对于任一实数![]() ,
,![]() 与
与![]() 的值至少有一个为正数,则实数
的值至少有一个为正数,则实数![]() 的取值范围是( C )
的取值范围是( C )
A. ![]() B.
B.![]() C.
C.
![]() D.
D.![]()
11.(辽宁2)若函数![]() 为偶函数,则a=( C
)
为偶函数,则a=( C
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.(辽宁4)已知![]() ,
,![]() ,
,
![]() ,
,![]() ,则( C )
,则( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
13.(全国Ⅰ1)函数![]() 的定义域为( D )
的定义域为( D )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
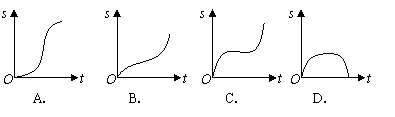
14.(全国Ⅰ2)汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程![]() 看作时间
看作时间![]() 的函数,其图像可能是( A )
的函数,其图像可能是( A )
15.(全国Ⅰ8)若函数![]() 的图象与函数
的图象与函数![]() 的图象关于直线
的图象关于直线![]() 对称,则
对称,则![]() ( A )
( A )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
16.(全国Ⅱ4)函数![]() 的图像关于( C )
的图像关于( C )
A.![]() 轴对称 B. 直线
轴对称 B. 直线![]() 对称
对称
C.
坐标原点对称 D. 直线![]() 对称
对称
17.(全国Ⅱ5)若![]() ,则( C )
,则( C )
A.![]() <
<![]() <
<![]() B.
B.![]() <
<![]() <
<![]() C.
C. ![]() <
<![]() <
<![]() D.
D. ![]() <
<![]() <
<![]()
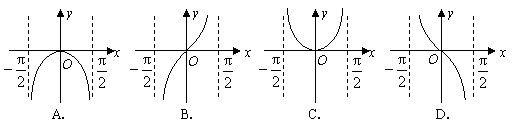
18.(山东3) 函数![]() 的图象是( A )
的图象是( A )
19.(山东5) 设函数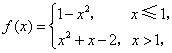 则
则![]() 的值为( A )
的值为( A )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
20.(山东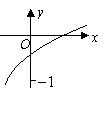 12) 已知函数
12) 已知函数![]() 的图象如图所示,则
的图象如图所示,则![]() 满足的关系是( A )
满足的关系是( A )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
21.(天津3 ) 函数![]() 的反函数是( A
)
的反函数是( A
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
22.(天津10) 设![]() ,若对于任意的
,若对于任意的![]() ,都有
,都有![]() 满足方程
满足方程![]() ,这时
,这时![]() 的取值的集合为( B
)
的取值的集合为( B
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
23.(重庆6)函数y=10x2-1 (0<x≤1=的反函数是 ( D )
(A)![]() (B)
(B)![]() (x>
(x>![]() )
)
(C) ![]() (
(![]() <x≤
<x≤![]() (D)
(D) ![]() (
(![]() <x≤
<x≤![]()
24.(湖北6).已知![]() 在R上是奇函数,
在R上是奇函数,
且![]() ( A )
( A )
A.-2 B.2 C.-98 D.98
25.(湖北8). 函数![]() 的定义域为 ( D )
的定义域为 ( D )
A.![]() B.
B. ![]()
C.![]() D.
D.![]()
26.(陕西7) 已知函数![]() ,
,![]() 是
是![]() 的反函数,若
的反函数,若![]() (
(![]() ),则
),则![]() 的值为( D )
的值为( D )
A.10 B.4 C.1 D.![]()
27.(陕西11) 定义在![]() 上的函数
上的函数![]() 满足
满足![]() (
(![]() ),
),![]() ,则
,则![]() 等于( A )
等于( A )
A.2 B.3 C.6 D.9
二、填空题
1.(安徽13)函数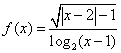 的定义域为
.
的定义域为
.![]()
2.(北京13)如图,函数![]() 的图象是折线段
的图象是折线段![]() ,其中
,其中![]() 的坐标分别为
的坐标分别为![]() ,则
,则![]() _________;2
_________;2
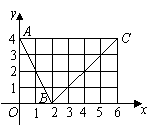 函数
函数![]() 在
在![]() 处的导数
处的导数![]() _________.
_________.![]()
3.(北京14).已知函数![]() ,对于
,对于![]() 上的任意
上的任意![]() ,有如下条件:
,有如下条件:
①![]() ; ②
; ②![]() ; ③
; ③![]() .
.
其中能使![]() 恒成立的条件序号是_________.②
恒成立的条件序号是_________.②
4.(湖南15)设![]() 表示不超x的最大整数,(如
表示不超x的最大整数,(如![]() )。对于给定的
)。对于给定的![]() ,
,
定义![]() 则
则![]() ________;
________;
当![]() 时,函数
时,函数![]() 的值域是_________________________。
的值域是_________________________。
![]()
![]()
 当
当![]() 时,
时,![]() 当
当![]() 时,
时,![]()
所以![]() 故函数
故函数![]() 的值域是
的值域是![]() .
.
5.(辽宁13)函数![]() 的反函数是
.
的反函数是
.![]()
6.(山东15) 已知![]() ,
,
则![]() 的
的
值等于 .2008
7.(上海4)若函数f(x)的反函数为![]() ,则
,则![]() .
.![]()
8.(浙江11)已知函数![]() ,则
,则![]() __________。2
__________。2
9.(重庆14)若![]() 则
则![]() =
.-23
=
.-23
10.(湖北13).方程![]() 的实数解的个数为
.
的实数解的个数为
.![]() 2
2
三、解答题
1.(江苏17)(14分)
某地有三家工厂,分别位于矩形ABCD的顶点A、B及CD的中点P处,已知AB=20km,BC=10km,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A、B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO、BO、OP,设排污管道的总长为ykm。
(1)按下列要求写出函数关系式:
①设∠BAO=θ(rad),将y表示成θ的函数关系式;
②设OP=x(km),将y表示成x的函数关系式;
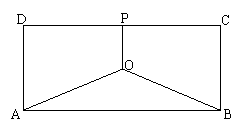 (2)请你选用(1)中的一个函数关系式,确定污水处理厂的位置,使三条排污管道总长度最短。
(2)请你选用(1)中的一个函数关系式,确定污水处理厂的位置,使三条排污管道总长度最短。
【解析】:本小题考查函数的概念、
解三角形、导数等基本知识,考查数学建模能力、
抽象概括能力和解决实际问题的能力。
(1)①由条件知PQ垂直平分AB,若∠BAO=θ(rad),则![]() ,
,
故![]()
又![]() ,所以
,所以![]()
所求函数关系式为![]()
②若OP=x(km),则OQ=10-x,所以![]()
所求函数关系式为![]()
(2)选择函数模型①,![]()
令![]() 得
得![]()
![]()
当![]() 时
时![]() ,y是θ的减函数;当
,y是θ的减函数;当![]() 时
时![]() ,y是θ的增函数;
,y是θ的增函数;
所以当![]() 时,
时,
此时点O位于线段AB的中垂线上,且距离AB边![]() km处。
km处。
2.(江苏20)(16分)
若![]() ,
,![]() ,
,![]() 为常数,且
为常数,且
(1)求![]() 对所有实数
对所有实数![]() 成立的充要条件(用
成立的充要条件(用![]() 表示)
表示)
(2)设![]() 为两实数,
为两实数,![]() 且
且![]() 若
若![]()
求证:![]() 在区间
在区间![]() 上的单调增区间的长度和为
上的单调增区间的长度和为![]() (闭区间
(闭区间![]() 的长度定义为
的长度定义为![]() )
)
【解析】:本小题考查充要条件、指数函数与绝对值函数、不等式的综合运用。
(1)![]() 恒成立
恒成立![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (*)
(*)
若![]() ,则(*)
,则(*)![]()
![]() ,显然成立;若
,显然成立;若![]() ,记
,记![]()
当![]() 时,
时,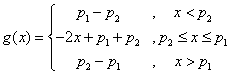
所以![]() ,故只需
,故只需![]() 。
。
当![]() 时,
时,
所以![]() ,故只需
,故只需![]() 。
。
综上所述,![]() 对所有实数
对所有实数![]() 成立的充要条件是
成立的充要条件是![]()
(2)10如果![]() ,则
,则![]() 的图像关于直线
的图像关于直线![]() 对称。(如图1)
对称。(如图1)
因为![]() ,所以区间
,所以区间![]() 关于直线
关于直线![]() 对称。
对称。
因为减区间为![]() ,增区间为
,增区间为![]() ,所以单调增区间的长度和为
,所以单调增区间的长度和为![]() 。
。
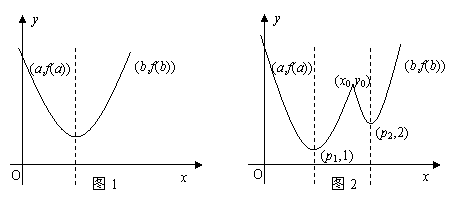
20如果![]() ,不妨设
,不妨设![]() ,则
,则![]() ,
,
于是当![]() 时,
时,![]() ,从而
,从而![]()
当![]() 时,
时,![]() ,从而
,从而![]()
当![]() 时,
时,![]() 及
及![]() ,
,
由方程![]() 得
得![]() ,(1)
,(1)
显然![]() ,表明
,表明![]() 在
在![]() 与
与![]() 之间。
之间。
所以
综上可知,在区间![]() 上,
上, (如图2)
(如图2)
故由函数![]() 及函数
及函数![]() 的单调性可知,
的单调性可知,![]() 在区间
在区间![]() 上的单调增区间的长度之和为
上的单调增区间的长度之和为![]() ,由
,由![]() ,即
,即![]() ,得
,得![]() (2)
(2)
故由(1)(2)得![]()
综合1020可知,![]() 在区间
在区间![]() 上的单调增区间的长度和为
上的单调增区间的长度和为![]() 。
。
 |