07 圆锥曲线
一、选择题
1.(北京3)“双曲线的方程为![]() ”是“双曲线的准线方程为
”是“双曲线的准线方程为![]() ”的( A )
”的( A )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
2.(福建12)双曲线![]() (a>0,b>0)的两个焦点为F1、F2,若P为其上一点,且PF1=2PE2,则双曲线离心率的取值范围为( B )
(a>0,b>0)的两个焦点为F1、F2,若P为其上一点,且PF1=2PE2,则双曲线离心率的取值范围为( B )
A.(1,3) B.(1,3) C.(3,+∞) D. [3,+∞]
3.(宁夏2)双曲线![]() 的焦距为( D )
的焦距为( D )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.(湖南10).双曲线![]() 的右支上存在一点,它到右焦点及左准线的距离相等,则双曲线离心率的取值范围是( C )
的右支上存在一点,它到右焦点及左准线的距离相等,则双曲线离心率的取值范围是( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.(江西7)已知![]() 、
、![]() 是椭圆的两个焦点,满足
是椭圆的两个焦点,满足![]() 的点
的点![]() 总在椭圆内部,则椭圆离心率的取值范围是( C )
总在椭圆内部,则椭圆离心率的取值范围是( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.(辽宁11)已知双曲线![]() 的一个顶点到它的一条渐近线的距离为
的一个顶点到它的一条渐近线的距离为![]() ,则
,则![]() ( D )
( D )
A.1 B.2 C.3 D.4
7.(全国Ⅱ11)设![]() 是等腰三角形,
是等腰三角形,![]() ,则以
,则以![]() 为焦点且过点
为焦点且过点![]() 的双曲线的离心率为( B )
的双曲线的离心率为( B )
A.![]() B.
B. ![]() C.
C. ![]() D.
D.![]()
8.(上海12)设![]() 是椭圆
是椭圆![]() 上的点.若
上的点.若![]() 是椭圆的两个焦点,则
是椭圆的两个焦点,则![]() 等于( D )
等于( D )
A.4 B.5 C.8 D.10
9.(四川11)已知双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() 为
为![]() 的右支上一点,且
的右支上一点,且![]() ,则
,则![]() 的面积等于( C )
的面积等于( C )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
10.(天津7) 设椭圆![]() 的右焦点与抛物线
的右焦点与抛物线![]() 的焦点相同,离心率为
的焦点相同,离心率为![]() ,则此椭圆的方程为( B
)
,则此椭圆的方程为( B
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.(浙江8)若双曲线![]() 的两个焦点到一条准线的距离之比为3:2,则双曲线的离心率是( D )
的两个焦点到一条准线的距离之比为3:2,则双曲线的离心率是( D )
(A)3 (B)5
(C)![]() (D)
(D)![]()
12.(重庆8)若双曲线![]() 的左焦点在抛物线y2=2px的准线上,则p的值为( C
)
的左焦点在抛物线y2=2px的准线上,则p的值为( C
)
(A)2 (B)3 (C)4 (D)4![]()
13.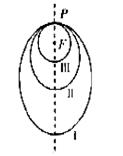 (湖北10).如图所示,“嫦娥一号”探月卫星沿地月转移轨道飞向月球,在月球附近一点P变轨进入以月球球心F为一个焦点的椭圆轨道I绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行,最终卫星在P点第三次变轨进入以F为圆形轨道Ⅲ绕月飞行,若用
(湖北10).如图所示,“嫦娥一号”探月卫星沿地月转移轨道飞向月球,在月球附近一点P变轨进入以月球球心F为一个焦点的椭圆轨道I绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行,最终卫星在P点第三次变轨进入以F为圆形轨道Ⅲ绕月飞行,若用![]() 和
和![]() 分别表示椭圆轨道I和Ⅱ的焦距,用
分别表示椭圆轨道I和Ⅱ的焦距,用![]() 和
和![]() 分别表示椭圆轨道I和Ⅱ的长轴的长,给出下列式子:
分别表示椭圆轨道I和Ⅱ的长轴的长,给出下列式子:
①![]() ②
②![]() ③
③![]() ④
④![]()
其中正确式子的序号是 ( B )
A.①③ B.②③
C.①④ D.②④
14.(陕西9) 双曲线![]() (
(![]() ,
,![]() )的左、右焦点分别是
)的左、右焦点分别是![]() ,过
,过![]() 作倾斜角为
作倾斜角为![]() 的直线交双曲线右支于
的直线交双曲线右支于![]() 点,若
点,若![]() 垂直于
垂直于![]() 轴,则双曲线的离心率为( B )
轴,则双曲线的离心率为( B )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题
1.(安徽14).已知双曲线![]() 的离心率是
的离心率是![]() 。则
。则![]() =
4
=
4
2.(宁夏15)过椭圆![]() 的右焦点作一条斜率为2的直线与椭圆交于
的右焦点作一条斜率为2的直线与椭圆交于![]() 两点,
两点,![]() 为坐标原点,则
为坐标原点,则![]() 的面积为
.
的面积为
.![]()
3.(江苏12)在平面直角坐标系中,椭圆![]() 的焦距为2,以O为圆心,
的焦距为2,以O为圆心,![]() 为半径的圆,过点
为半径的圆,过点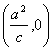 作圆的两切线互相垂直,则离心率
作圆的两切线互相垂直,则离心率![]() =
=
![]()
4.(江西14)已知双曲线![]() 的两条渐近线方程为
的两条渐近线方程为![]() ,若顶点到渐近线的距离为1,则双曲线方程为
.
,若顶点到渐近线的距离为1,则双曲线方程为
.![]()
5.(全国Ⅰ14)已知抛物线![]() 的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为
.
的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为
.![]()
6.(全国Ⅰ15)在![]() 中,
中,![]() ,
,![]() .若以
.若以![]() 为焦点的椭圆经过点
为焦点的椭圆经过点![]() ,则该椭圆的离心率
,则该椭圆的离心率![]() .
.![]()
7.(全国Ⅱ15)已知![]() 是抛物线
是抛物线![]() 的焦点,
的焦点,![]() 是
是![]() 上的两个点,线段AB的中点为
上的两个点,线段AB的中点为![]() ,则
,则![]() 的面积等于 .2
的面积等于 .2
8.(山东13) 已知圆![]() .以圆
.以圆![]() 与坐标轴的交点分别作为双曲线的一个焦点和顶点,则适合上述条件的双曲线的标准方程为
.
与坐标轴的交点分别作为双曲线的一个焦点和顶点,则适合上述条件的双曲线的标准方程为
.![]()
9.(上海6)若直线![]() 经过抛物线
经过抛物线![]() 的焦点,则实数
的焦点,则实数![]() .-1
.-1
10.(浙江13)已知![]() 为椭圆
为椭圆![]() 的两个焦点,过
的两个焦点,过![]() 的直线交椭圆于A、B两点
的直线交椭圆于A、B两点
若![]() ,则
,则![]() = 。8
= 。8
三、解答题
1.(安徽22).(本小题满分14分)
设椭圆![]() 其相应于焦点
其相应于焦点![]() 的准线方程为
的准线方程为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知过点![]() 倾斜角为
倾斜角为![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 两点,求证:
两点,求证:
![]() ;
;
(Ⅲ)过点![]() 作两条互相垂直的直线分别交椭圆
作两条互相垂直的直线分别交椭圆![]() 于
于![]() 和
和![]() ,求
,求![]() 的最小值
的最小值
解 :(1)由题意得:
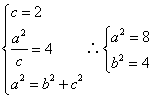
![]() 椭圆
椭圆![]() 的方程为
的方程为![]()
(2)方法一:由(1)知![]() 是椭圆
是椭圆![]() 的左焦点,离心率
的左焦点,离心率![]()
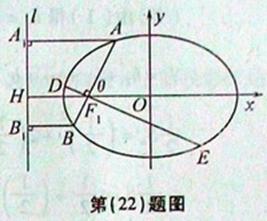
设![]() 为椭圆的左准线。则
为椭圆的左准线。则![]()
作![]() ,
,![]() 与
与![]() 轴交于点H(如图)
轴交于点H(如图)
![]() 点A在椭圆上
点A在椭圆上
![]()
![]()
![]()
![]()
同理 ![]()
![]() 。
。
方法二:
当![]() 时,记
时,记![]() ,则
,则![]()
将其代入方程 ![]() 得
得 ![]()
设 ![]() ,则
,则![]() 是此二次方程的两个根.
是此二次方程的两个根.
![]()
![]()
![]() ................(1)
................(1)
![]() 代入(1)式得
代入(1)式得
![]() ........................(2)
........................(2)
当![]() 时,
时,![]() 仍满足(2)式。
仍满足(2)式。
![]()
(3)设直线![]() 的倾斜角为
的倾斜角为![]() ,由于
,由于![]() 由(2)可得
由(2)可得
![]() ,
,![]()
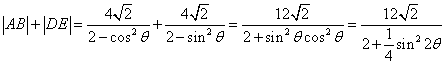
当![]() 时,
时,![]() 取得最小值
取得最小值![]()
2.(北京19)(本小题共14分)
已知![]() 的顶点
的顶点![]() 在椭圆
在椭圆![]() 上,
上,![]() 在直线
在直线![]() 上,且
上,且![]() .
.
(Ⅰ)当![]() 边通过坐标原点
边通过坐标原点![]() 时,求
时,求![]() 的长及
的长及![]() 的面积;
的面积;
(Ⅱ)当![]() ,且斜边
,且斜边![]() 的长最大时,求
的长最大时,求![]() 所在直线的方程.
所在直线的方程.
解:(Ⅰ)因为![]() ,且
,且![]() 边通过点
边通过点![]() ,所以
,所以![]() 所在直线的方程为
所在直线的方程为![]() .
.
设![]() 两点坐标分别为
两点坐标分别为![]() .
.
由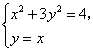 得
得![]() .
.
所以![]() .
.
又因为![]() 边上的高
边上的高![]() 等于原点到直线
等于原点到直线![]() 的距离.
的距离.
所以![]() ,
,![]() .
.
(Ⅱ)设![]() 所在直线的方程为
所在直线的方程为![]() ,
,
由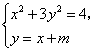 得
得![]() .
.
因为![]() 在椭圆上,
在椭圆上,
所以![]() .
.
设![]() 两点坐标分别为
两点坐标分别为![]() ,
,
则![]() ,
,![]() ,
,
所以![]() .
.
又因为![]() 的长等于点
的长等于点![]() 到直线
到直线![]() 的距离,即
的距离,即![]() .
.
所以![]() .
.
所以当![]() 时,
时,![]() 边最长,(这时
边最长,(这时![]() )
)
此时![]() 所在直线的方程为
所在直线的方程为![]() .
.
3. (福建22)(本小题满分14分)
(福建22)(本小题满分14分)
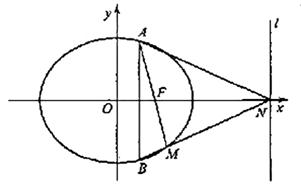
如图,椭圆![]() (a>b>0)的一个焦点为F(1,0),且过点(2,0).
(a>b>0)的一个焦点为F(1,0),且过点(2,0).
(Ⅰ)求椭圆C的方程;
(Ⅱ)若AB为垂直于x轴的动弦,直线l:x=4与x轴交于点N,直线AF与BN交于点M.
(ⅰ)求证:点M恒在椭圆C上;
(ⅱ)求△AMN面积的最大值.
解法一:
(Ⅰ)由题设a=2,c=1,从而b2=a2-c2=3,
所以椭圆C前方程为![]() .
.
(Ⅱ)(i)由题意得F(1,0),N(4,0).
设A(m,n),则B(m,-n)(n≠0),![]() =1. ……①
=1. ……①
AF与BN的方程分别为:n(x-1)-(m-1)y=0,
n(x-4)-(m-4)y=0.
![]() 设M(x0,y0),则有 n(x0-1)-(m-1)y0=0, ……②
设M(x0,y0),则有 n(x0-1)-(m-1)y0=0, ……②
n(x0-4)+(m-4)y0=0, ……③
由②,③得
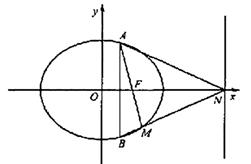 x0=
x0=![]() .
.
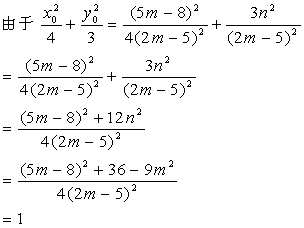
所以点M恒在椭圆G上.
(ⅱ)设AM的方程为x=xy+1,代入![]() =1得(3t2+4)y2+6ty-9=0.
=1得(3t2+4)y2+6ty-9=0.
设A(x1,y1),M(x2,y2),则有:y1+y2=![]()
y1-y2=![]()
令3t2+4=λ(λ≥4),则
y1-y2=![]()
因为λ≥4,0<![]()
y1-y2有最大值3,此时AM过点F.
△AMN的面积S△AMN=![]()
解法二:
(Ⅰ)问解法一:
(Ⅱ)(ⅰ)由题意得F(1,0),N(4,0).
设A(m,n),则B(m,-n)(n≠0), ![]() ……①
……①
AF与BN的方程分别为:n(x-1)-(m-1)y=0, ……②
n(x-4)-(m-4)y=0, ……③
由②,③得:当≠![]() .
……④
.
……④
由④代入①,得![]() =1(y≠0).
=1(y≠0).
当x=![]() 时,由②,③得:
时,由②,③得: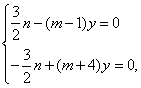
解得![]() 与a≠0矛盾.
与a≠0矛盾.
所以点M的轨迹方程为![]() 即点M恒在锥圆C上.
即点M恒在锥圆C上.
(Ⅱ)同解法一.
4.(广东20)(本小题满分14分)
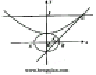 设b
设b![]() 0,椭圆方程为
0,椭圆方程为![]() =1,抛物线方程为x2=8(y-b).如图6所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G.已知抛物线在点G的切线经过椭圆的右焦点F1.
=1,抛物线方程为x2=8(y-b).如图6所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G.已知抛物线在点G的切线经过椭圆的右焦点F1.
(1)求满足条件的椭圆方程和抛物线方程;
(2)设A1B分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点P,使得![]() 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
解:(1)由![]() 得
得 ![]()
当![]() 时,
时,![]() ,
,![]() G点的坐标为(4,b+2)
G点的坐标为(4,b+2)
![]() ,
, ![]()
过点G的切线方程为![]() ,即
,即![]() ,
,
令y=0得 ![]() ,
,![]()
![]() 点的坐标为 (2-b,0);
点的坐标为 (2-b,0);
由椭圆方程得![]() 点的坐标为(b,0),
点的坐标为(b,0),
![]()
![]() 即 b=1,
即 b=1,
因此所求的椭圆方程及抛物线方程分别为![]() 和
和![]() .
.
(2)![]() 过A作x轴的垂线与抛物线只有一个交点P,
过A作x轴的垂线与抛物线只有一个交点P,
![]() 以
以![]() 为直角的
为直角的![]() 只有一个;
只有一个;
同理以![]() 为直角的
为直角的![]() 只有一个;
只有一个;
若以![]() 为直角, 设P点的坐标为
为直角, 设P点的坐标为![]() ,则A、B坐标分别
,则A、B坐标分别
为![]() 、
、![]()
由![]() 得
得![]() ,
,
关于![]() 的一元二次方程有一解,
的一元二次方程有一解,![]() x有二解,即以
x有二解,即以![]() 为直角的
为直角的![]() 有二个;
有二个;
因此抛物线上共存在4个点使![]() 为直角三角形.
为直角三角形.
5.(宁夏23)(本小题满分10分)(选修4-4;坐标系与参数方程)
已知曲线C1:![]() (
(![]() 为参数),曲线C2:
为参数),曲线C2: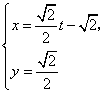 (t为参数).
(t为参数).
(Ⅰ)指出C1,C2各是什么曲线,并说明C1与C2公共点的个数;
(Ⅱ)若把C1,C2上各点的纵坐标都压缩为原来的一半,分别得到曲线![]() .写出
.写出![]() 的参数方程.
的参数方程.![]() 与
与![]() 公共点的个数和C
公共点的个数和C![]() 公共点的个数是否相同?说明你的理由.
公共点的个数是否相同?说明你的理由.
解:(Ⅰ)![]() 是圆,
是圆,![]() 是直线. 2分
是直线. 2分
![]() 的普通方程为
的普通方程为![]() ,圆心
,圆心![]() ,半径
,半径![]() .
.
![]() 的普通方程为
的普通方程为![]() .
.
因为圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
所以![]() 与
与![]() 只有一个公共点.····················································································· 4分
只有一个公共点.····················································································· 4分
(Ⅱ)压缩后的参数方程分别为
![]() :
: (
(![]() 为参数)
为参数) ![]() :
: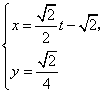 (t为参数)························· 8分
(t为参数)························· 8分
化为普通方程为:![]() :
:![]() ,
,![]() :
:![]() ,
,
联立消元得![]() ,
,
其判别式![]() ,
,
所以压缩后的直线![]() 与椭圆
与椭圆![]() 仍然只有一个公共点,和
仍然只有一个公共点,和![]() 与
与![]() 公共点个数相同.10分
公共点个数相同.10分
6.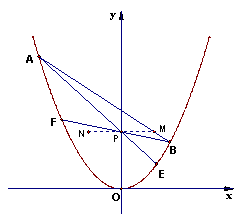 (江西22)已知抛物线
(江西22)已知抛物线![]() 和三个点
和三个点
![]()
![]() ,过点
,过点![]() 的一条直线交抛物线于
的一条直线交抛物线于![]() 、
、![]() 两点,
两点,![]() 的延长线分别交曲线
的延长线分别交曲线![]() 于
于![]() .
.
(1)证明![]() 三点共线;
三点共线;
(2)如果![]() 、
、![]() 、
、![]() 、
、![]() 四点共线,问:是否存在
四点共线,问:是否存在![]() ,使以线段
,使以线段![]() 为直径的圆与抛物线有异于
为直径的圆与抛物线有异于![]() 、
、![]() 的交点?如果存在,求出
的交点?如果存在,求出![]() 的取值范围,并求出该交点到直线
的取值范围,并求出该交点到直线![]() 的距离;若不存在,请说明理由.
的距离;若不存在,请说明理由.
(1)证明:设![]() ,
,![]()
则直线![]() 的方程:
的方程:![]()
即:![]()
因![]() 在
在![]() 上,所以
上,所以![]() ①
①
又直线![]() 方程:
方程:![]()
由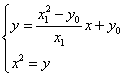 得:
得:![]()
所以![]()
同理,![]()
所以直线![]() 的方程:
的方程:![]()
令![]() 得
得![]()
将①代入上式得![]() ,即
,即![]() 点在直线
点在直线![]() 上
上
所以![]() 三点共线
三点共线
(2)解:由已知![]() 共线,所以
共线,所以![]()
以![]() 为直径的圆的方程:
为直径的圆的方程:![]()
由 得
得![]()
所以![]() (舍去),
(舍去),![]()
要使圆与抛物线有异于![]() 的交点,则
的交点,则![]()
所以存在![]() ,使以
,使以![]() 为直径的圆与抛物线有异于
为直径的圆与抛物线有异于![]() 的交点
的交点![]()
则![]() ,所以交点
,所以交点![]() 到
到![]() 的距离为
的距离为![]()
7.(江苏选修) 在平面直角坐标系![]() 中,点
中,点![]() 是椭圆
是椭圆![]() 上的一个动点,求
上的一个动点,求![]() 的最大值.
的最大值.
解: 因椭圆![]() 的参数方程为
的参数方程为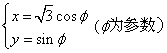
故可设动点![]() 的坐标为
的坐标为![]() ,其中
,其中![]() .
.
因此![]()
所以。当![]() 是,
是,![]() 取最大值2
取最大值2
8.(湖南19)(本小题满分13分)
已知椭圆的中心在原点,一个焦点是F(2,0),且两条准线间的距离为λ(λ>4).
(Ⅰ)求椭圆的方程;
(Ⅱ)若存在过点A(1,0)的直线l,使点F关于直线l的对称点在椭圆上,求λ的取值范围.
解 (Ⅰ)设椭圆的方程为![]() (a>b>0).
(a>b>0).
由条件知c=2,且![]() =λ,所以a2=λ,
=λ,所以a2=λ,
b2=a2-c2=λ-4.故椭圆的方程是![]()
![]()
(Ⅱ)依题意,直线l的斜率存在且不为0,记为k,则直线l的方程是y=k(x-1).设点F(2,0)关于直线l的对称点为F2(x0,y0),则
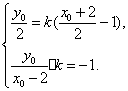 解得
解得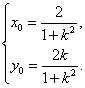
因为点F′(x0,y0)在椭圆上,所以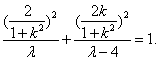 即
即
λ(λ-4)k4+2λ(λ-6)k2+(λ-4)2=0.
设k2=t,则λ(λ-4)t2+2λ(λ-6)t+(λ-4)2=0.
因为λ>4,所以![]() >0.
>0.
9.(辽宁21).(本小题满分12分)
在平面直角坐标系![]() 中,点P到两点
中,点P到两点![]() ,
,![]() 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为![]() .
.
(Ⅰ)写出C的方程;
(Ⅱ)设直线![]() 与C交于A,B两点.k为何值时
与C交于A,B两点.k为何值时![]()
![]()
![]() ?此时
?此时![]() 的值是多少?
的值是多少?
解:(Ⅰ)设P(x,y),由椭圆定义可知,点P的轨迹C是以![]() 为焦点,长半轴为2的椭圆.它的短半轴
为焦点,长半轴为2的椭圆.它的短半轴![]() ,
,
故曲线C的方程为![]() .··················································································· 4分
.··················································································· 4分
(Ⅱ)设![]() ,其坐标满足
,其坐标满足
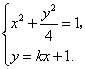
消去y并整理得![]() ,
,
故![]() .······································································· 6分
.······································································· 6分
![]() ,即
,即![]() .
.
而![]() ,
,
于是![]() .
.
所以![]() 时,
时,![]() ,故
,故![]() .························································ 8分
.························································ 8分
当![]() 时,
时,![]() ,
,![]() .
.
![]() ,
,
而![]()
![]() ,
,
所以![]() . 12分
. 12分
10.(全国Ⅰ22)(本小题满分12分)
双曲线的中心为原点![]() ,焦点在
,焦点在![]() 轴上,两条渐近线分别为
轴上,两条渐近线分别为![]() ,经过右焦点
,经过右焦点![]() 垂直于
垂直于![]() 的直线分别交
的直线分别交![]() 于
于![]() 两点.已知
两点.已知![]() 成等差数列,且
成等差数列,且![]() 与
与![]() 同向.
同向.
(Ⅰ)求双曲线的离心率;
(Ⅱ)设![]() 被双曲线所截得的线段的长为4,求双曲线的方程.
被双曲线所截得的线段的长为4,求双曲线的方程.
解:(1)设![]() ,
,![]() ,
,![]()
由勾股定理可得:![]()
得:![]() ,
,![]() ,
,![]()
由倍角公式![]()
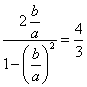 ,解得
,解得![]()
则离心率![]() .
.
(2)过![]() 直线方程为
直线方程为![]()
与双曲线方程![]() 联立
联立
将![]() ,
,![]() 代入,化简有
代入,化简有![]()
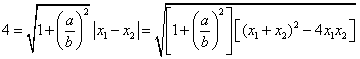
将数值代入,有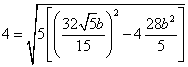
解得![]()
最后求得双曲线方程为:![]() .
.
11.(全国Ⅱ22)(本小题满分12分)
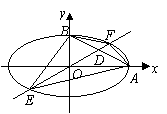
设椭圆中心在坐标原点,![]() 是它的两个顶点,直线
是它的两个顶点,直线![]() 与AB相交于点D,与椭圆相交于E、F两点.
与AB相交于点D,与椭圆相交于E、F两点.
(Ⅰ)若![]() ,求
,求![]() 的值;
的值;
(Ⅱ)求四边形![]() 面积的最大值.
面积的最大值.
(Ⅰ)解:依题设得椭圆的方程为![]() ,
,
直线![]() 的方程分别为
的方程分别为![]() ,
,![]() .············································ 2分
.············································ 2分
如图,设![]() ,其中
,其中![]() ,
,
 且
且![]() 满足方程
满足方程![]() ,
,
故![]() .①
.①
由![]() 知
知![]() ,得
,得![]() ;
;
由![]() 在
在![]() 上知
上知![]() ,得
,得![]() .
.
所以![]() ,
,
化简得![]() ,
,
解得![]() 或
或![]() .··································································································· 6分
.··································································································· 6分
(Ⅱ)解法一:根据点到直线的距离公式和①式知,点![]() 到
到![]() 的距离分别为
的距离分别为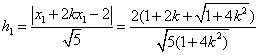 ,
,
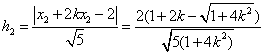 .································································ 9分
.································································ 9分
又![]() ,所以四边形
,所以四边形![]() 的面积为
的面积为
![]()
![]()
![]()
![]()
![]() ,
,
当![]() ,即当
,即当![]() 时,上式取等号.所以
时,上式取等号.所以![]() 的最大值为
的最大值为![]() .····························· 12分
.····························· 12分
解法二:由题设,![]() ,
,![]() .
.
设![]() ,
,![]() ,由①得
,由①得![]() ,
,![]() ,
,
故四边形![]() 的面积为
的面积为
![]()
![]() ···················································································································· 9分
···················································································································· 9分
![]()
![]()
![]()
![]() ,
,
当![]() 时,上式取等号.所以
时,上式取等号.所以![]() 的最大值为
的最大值为![]() . 12分
. 12分
12.(山东22.(本小题满分14分)
已知曲线![]() 所围成的封闭图形的面积为
所围成的封闭图形的面积为![]() ,曲线
,曲线![]() 的内切圆半径为
的内切圆半径为![]() .记
.记![]() 为以曲线
为以曲线![]() 与坐标轴的交点为顶点的椭圆.
与坐标轴的交点为顶点的椭圆.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设![]() 是过椭圆
是过椭圆![]() 中心的任意弦,
中心的任意弦,![]() 是线段
是线段![]() 的垂直平分线.
的垂直平分线.![]() 是
是![]() 上异于椭圆中心的点.
上异于椭圆中心的点.
(1)若![]() (
(![]() 为坐标原点),当点
为坐标原点),当点![]() 在椭圆
在椭圆![]() 上运动时,求点
上运动时,求点![]() 的轨迹方程;
的轨迹方程;
(2)若![]() 是
是![]() 与椭圆
与椭圆![]() 的交点,求
的交点,求![]() 的面积的最小值.
的面积的最小值.
解:(Ⅰ)由题意得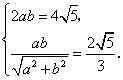
又![]() ,
,
解得![]() ,
,![]() .
.
因此所求椭圆的标准方程为![]() .
.
(Ⅱ)(1)假设![]() 所在的直线斜率存在且不为零,设
所在的直线斜率存在且不为零,设![]() 所在直线方程为
所在直线方程为![]() ,
,
![]() .
.
解方程组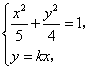 得
得![]() ,
,![]() ,
,
所以![]() .
.
设![]() ,由题意知
,由题意知![]() ,
,
所以![]() ,即
,即![]() ,
,
因为![]() 是
是![]() 的垂直平分线,
的垂直平分线,
所以直线![]() 的方程为
的方程为![]() ,
,
即![]() ,
,
因此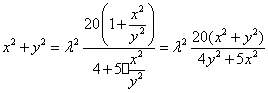 ,
,
又![]() ,
,
所以![]() ,
,
故![]() .
.
又当![]() 或不存在时,上式仍然成立.
或不存在时,上式仍然成立.
综上所述,![]() 的轨迹方程为
的轨迹方程为![]() .
.
(2)当![]() 存在且
存在且![]() 时,由(1)得
时,由(1)得![]() ,
,![]() ,
,
由 解得
解得![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
解法一:由于![]()
![]()
![]()
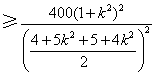
![]() ,
,
当且仅当![]() 时等号成立,即
时等号成立,即![]() 时等号成立,此时
时等号成立,此时![]() 面积的最小值是
面积的最小值是![]() .
.
当![]() ,
,![]() .
.
当![]() 不存在时,
不存在时,![]() .
.
综上所述,![]() 的面积的最小值为
的面积的最小值为![]() .
.
解法二:因为
![]() ,
,
又![]() ,
,![]() ,
,
当且仅当![]() 时等号成立,即
时等号成立,即![]() 时等号成立,
时等号成立,
此时![]() 面积的最小值是
面积的最小值是![]() .
.
当![]() ,
,![]() .
.
当![]() 不存在时,
不存在时,![]() .
.
综上所述,![]() 的面积的最小值为
的面积的最小值为![]() .
.
13.(上海20)(本题满分16分)本题共有3个小题,第1小题满分3分,第2小题满分6分,第3小题满分7分.
已知双曲线![]() .
.
(1)求双曲线![]() 的渐近线方程;
的渐近线方程;
(2)已知点![]() 的坐标为
的坐标为![]() .设
.设![]() 是双曲线
是双曲线![]() 上的点,
上的点,![]() 是点
是点![]() 关于原点的对称点.
关于原点的对称点.
记![]() .求
.求![]() 的取值范围;
的取值范围;
(3)已知点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() 为双曲线
为双曲线![]() 上在第一象限内的点.记
上在第一象限内的点.记![]() 为经过原点与点
为经过原点与点![]() 的直线,
的直线,![]() 为
为![]() 截直线
截直线![]() 所得线段的长.试将
所得线段的长.试将![]() 表示为直线
表示为直线![]() 的斜率
的斜率![]() 的函数.
的函数.
【解】(1)所求渐近线方程为![]() ……………...3分
……………...3分
(2)设P的坐标为![]() ,则Q的坐标为
,则Q的坐标为![]() , …………….4分
, …………….4分
![]()
![]() ……………7分
……………7分
![]()
![]() 的取值范围是
的取值范围是![]() ……………9分
……………9分
(3)若P为双曲线C上第一象限内的点,
则直线![]() 的斜率
的斜率![]() ……………11分
……………11分
由计算可得,当![]()
当![]() ……………15分
……………15分
∴ s表示为直线![]() 的斜率k的函数是
的斜率k的函数是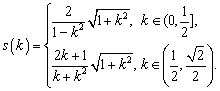 ….16分
….16分
14.(四川22)(本小题满分14分)
设椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,离心率
,离心率![]() ,点
,点![]() 到右准线为
到右准线为![]() 的距离为
的距离为![]()
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)设![]() 是
是![]() 上的两个动点,
上的两个动点,![]() ,
,
证明:当![]() 取最小值时,
取最小值时,![]()
【解】:因为![]() ,
,![]() 到
到![]() 的距离
的距离![]() ,所以由题设得
,所以由题设得
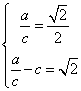 解得
解得![]()
由![]() ,得
,得![]()
(Ⅱ)由![]() 得
得![]() ,
,![]() 的方程为
的方程为![]()
故可设![]()
由知![]() 知
知 ![]()
得![]() ,所以
,所以![]()
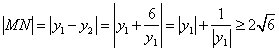
当且仅当![]() 时,上式取等号,此时
时,上式取等号,此时![]()
所以,![]()
![]()
![]()
15.(天津22)(本小题满分14分)
已知中心在原点的双曲线![]() 的一个焦点是
的一个焦点是![]() ,一条渐近线的方程是
,一条渐近线的方程是![]() .
.
(Ⅰ)求双曲线![]() 的方程;
的方程;
(Ⅱ)若以![]() 为斜率的直线
为斜率的直线![]() 与双曲线
与双曲线![]() 相交于两个不同的点
相交于两个不同的点![]() ,且线段
,且线段![]() 的垂直平分线与两坐标轴围成的三角形的面积为
的垂直平分线与两坐标轴围成的三角形的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
(Ⅰ)解:设双曲线![]() 的方程为
的方程为![]() ,由题设得
,由题设得
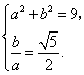 解得
解得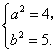
所以双曲线![]() 的方程为
的方程为![]() .
.
(Ⅱ)解:设直线![]() 的方程为
的方程为![]() ,点
,点![]() ,
,![]() 的坐标满足方程组
的坐标满足方程组
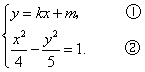
将①式代入②式,得![]() ,整理得
,整理得
![]() .
.
此方程有两个不等实根,于是![]() ,且
,且
![]() .整理得
.整理得
![]() . ③
. ③
由根与系数的关系可知线段![]() 的中点坐标
的中点坐标![]() 满足
满足
![]() ,
,![]() .
.
从而线段![]() 的垂直平分线的方程为
的垂直平分线的方程为
![]() .
.
此直线与![]() 轴,
轴,![]() 轴的交点坐标分别为
轴的交点坐标分别为![]() ,
,![]() .由题设可得
.由题设可得
![]() .
.
整理得
![]() ,
,![]() .
.
将上式代入③式得![]() ,
,
整理得
![]() ,
,![]() .
.
解得![]() 或
或![]() .
.
所以![]() 的取值范围是
的取值范围是 .
.
16.(浙江22)(本题15分)已知曲线C是到点P(![]() )和到直线
)和到直线![]() 距离相等的点的轨迹。
距离相等的点的轨迹。![]() 是过点Q(-1,0)的直线,M是C上(不在
是过点Q(-1,0)的直线,M是C上(不在![]() 上)的动点;A、B在
上)的动点;A、B在![]() 上,
上,![]() 轴(如图)。
轴(如图)。
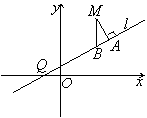 (Ⅰ)求曲线C的方程;
(Ⅰ)求曲线C的方程;
(Ⅱ)求出直线![]() 的方程,使得
的方程,使得![]() 为常数。
为常数。
(Ⅰ)解:设![]() 为
为![]() 上的点,则
上的点,则
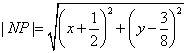 ,
,
![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
由题设得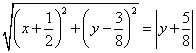 .
.
化简,得曲线![]() 的方程为
的方程为![]() .
.
(Ⅱ)解法一:
设 ,直线
,直线![]() ,则
,则

![]() ,从而
,从而
![]() .
.
在![]() 中,因为
中,因为
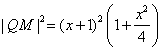 ,
,
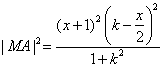 .
.
所以![]() .
.
![]() ,
,
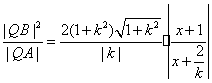 .
.
当![]() 时,
时,![]() ,
,
从而所求直线![]() 方程为
方程为![]() .
.
解法二:设 ,直线
,直线![]() ,则
,则![]() ,从而
,从而
![]() .
.
过![]() 垂直于
垂直于![]() 的直线
的直线![]() .
.
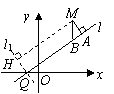 因为
因为![]() ,所以
,所以![]() ,
,
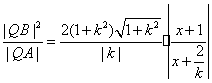 .
.
当![]() 时,
时,![]() ,
,
从而所求直线![]() 方程为
方程为![]() .
.
17.(重庆21)(本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分.)
如题(21)图,M(-2,0)和N(2,0)是平面上的两点,动点P满足: ![]()
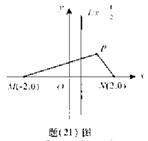
(Ⅰ)求点P的轨迹方程;
(Ⅱ)设d为点P到直线l:
![]() 的距离,若
的距离,若![]() ,求
,求![]() 的值.
的值.
解:(I)由双曲线的定义,点P的轨迹是以M、N为焦点,实轴长2a=2的双曲线.
因此半焦距c=2,实半轴a=1,从而虚半轴b=![]() ,
,
所以双曲线的方程为x2-![]() =1.
=1.
(II)解法一:
由(I)由双曲线的定义,点P的轨迹是以M、N为焦点,实轴长2a=2的双曲线.
因此半焦距e=2,实半轴a=1,从而虚半轴b=![]() .
.
R所以双曲线的方程为x2-![]() =1.
=1.
(II)解法一:
由(I)及答(21)图,易知PN![]() 1,因PM=2PN2, ①
1,因PM=2PN2, ①
知PM>PN,故P为双曲线右支上的点,所以PM=PN+2. ②
将②代入①,得2PN2-PN-2=0,解得PN=![]() ,所以
,所以
PN=![]() .
.
因为双曲线的离心率e=![]() =2,直线l:x=
=2,直线l:x=![]() 是双曲线的右准线,故
是双曲线的右准线,故![]() =e=2,
=e=2,
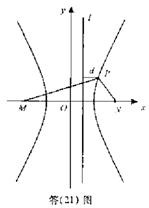
所以d=![]() PN,因此
PN,因此
![]()
 解法:
解法:
设P(x,y),因PN![]() 1知
1知
PM=2PN2![]() 2PN>PN,
2PN>PN,
故P在双曲线右支上,所以x![]() 1.
1.
由双曲线方程有y2=3x2-3.
因此![]()
![]()
从而由PM=2PN2得
2x+1=2(4x2-4x+1),即8x2-10x+1=0.
所以x=![]() (舍去x=
(舍去x=![]() ).
).
有PM=2x+1=![]()
d=x-![]() =
=![]() .
.
故![]()
18.(湖北20)(本小题满分13分)
已知双同线![]() 的两个焦点为
的两个焦点为![]()
的曲线C上.
(Ⅰ)求双曲线C的方程;
(Ⅱ)记O为坐标原点,过点Q (0,2)的直线l与双曲线C相交于不同的两点E、F,若△OEF的面积为![]() 求直线l的方程
求直线l的方程
(Ⅰ)解法1:依题意,由a2+b2=4,得双曲线方程为![]() (0<a2<4=,
(0<a2<4=,
将点(3,![]() )代入上式,得
)代入上式,得![]() .解得a2=18(舍去)或a2=2,
.解得a2=18(舍去)或a2=2,
故所求双曲线方程为![]()
解法2:依题意得,双曲线的半焦距c=2.
2a=PF1-PF2=![]()
∴a2=2,b2=c2-a2=2.
∴双曲线C的方程为![]()
(Ⅱ)解法1:依题意,可设直线l的方程为y=kx+2,代入双曲线C的方程并整理,
得(1-k2)x2-4kx-6=0.
∵直线I与双曲线C相交于不同的两点E、F,
∴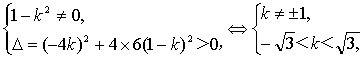
∴k∈(-![]() )∪(1,
)∪(1,![]() ).
).
设E(x1,y1),F(x2,y2),则由①式得x1+x2=![]() 于是
于是
EF=![]()
=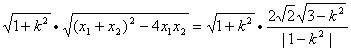
而原点O到直线l的距离d=![]() ,
,
∴SΔOEF=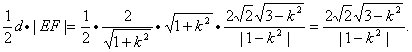
若SΔOEF=![]() ,即
,即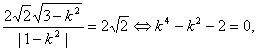 解得k=±
解得k=±![]() ,
,
满足②.故满足条件的直线l有两条,其方程分别为y=![]() 和
和![]()
解法2:依题意,可设直线l的方程为y=kx+2,代入双曲线C的方程并整理,
得(1-k2)x2-4kx-6=0. ①
∵直线l与比曲线C相交于不同的两点E、F,
∴
∴k∈(-![]() )∪(1,
)∪(1,![]() ). ②
). ②
设E(x1,y1),F(x2,y2),则由①式得
x1-x2=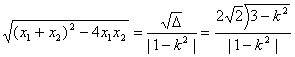 . ③
. ③
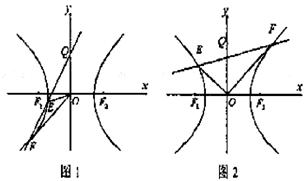
当E、F在同一支上时(如图1所示),
SΔOEF=SΔOQF-SΔOQE=![]() ;
;
当E、F在不同支上时(如图2所示),
SΔOEF=SΔOQF+SΔOQE=![]()
综上得SΔOEF=![]() ,于是
,于是
由OQ=2及③式,得SΔOEF=![]() .
.
若SΔOEF=2![]() ,即
,即![]() ,解得k=±
,解得k=±![]() ,满足②.
,满足②.
故满足条件的直线l有两条,基方程分别为y=![]() 和y=
和y=![]()
18.(陕西21)(本小题满分12分)
已知抛物线![]() :
:![]() ,直线
,直线![]() 交
交![]() 于
于![]() 两点,
两点,![]() 是线段
是线段![]() 的中点,过
的中点,过![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 于点
于点![]() .
.
(Ⅰ)证明:抛物线![]() 在点
在点![]() 处的切线与
处的切线与![]() 平行;
平行;
(Ⅱ)是否存在实数![]() 使
使![]() ,若存在,求
,若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
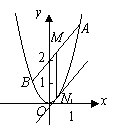
解法一:(Ⅰ)如图,设![]() ,
,![]() ,把
,把![]() 代入
代入![]() 得
得![]() ,
,
 由韦达定理得
由韦达定理得![]() ,
,![]() ,
,
![]()
![]() ,
,![]()
![]() 点的坐标为
点的坐标为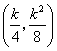 .
.
设抛物线在点![]() 处的切线
处的切线![]() 的方程为
的方程为![]() ,
,
将![]() 代入上式得
代入上式得![]() ,
,
![]() 直线
直线![]() 与抛物线
与抛物线![]() 相切,
相切,
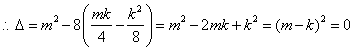 ,
,![]() .
.
即![]() .
.
(Ⅱ)假设存在实数![]() ,使
,使![]() ,则
,则![]() ,又
,又![]() 是
是![]() 的中点,
的中点,
![]() .
.
由(Ⅰ)知![]()
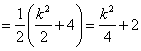 .
.
![]()
![]() 轴,
轴,![]() .
.
又![]()
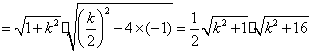 .
.
![]() ,解得
,解得![]() .
.
即存在![]() ,使
,使![]() .
.
解法二:(Ⅰ)如图,设![]() ,把
,把![]() 代入
代入![]() 得
得
![]() .由韦达定理得
.由韦达定理得![]() .
.
![]()
![]() ,
,![]()
![]() 点的坐标为
点的坐标为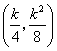 .
.![]() ,
,![]() ,
,
![]() 抛物线在点
抛物线在点![]() 处的切线
处的切线![]() 的斜率为
的斜率为![]() ,
,![]() .
.
(Ⅱ)假设存在实数![]() ,使
,使![]() .
.
由(Ⅰ)知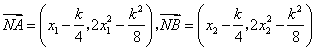 ,则
,则
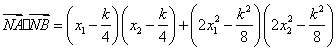
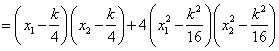
![]()
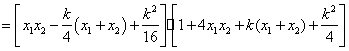

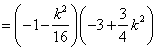
![]() ,
,
![]() ,
,![]() ,解得
,解得![]() .
.
即存在![]() ,使
,使![]() .
.