高一数学月考
一.填空题
1.函数![]() ,则
,则![]() =
=
2.函数![]() 的定义域是
的定义域是
3.函数![]() ,
,![]() ,则函数
,则函数![]()
4.已知函数g(x)=1-2x, ,![]() ,则
,则![]() =
=
5.设f(x)是定义在R上的奇函数,且其图象关于直线![]() 对称,则f (1) =________.
对称,则f (1) =________.
6.函数![]() 在
在![]() 上的零点是_____________________(精确到
上的零点是_____________________(精确到![]() )
)
7.若函数f(x)是定义在R上的偶函数,在![]() 上是减函数,且f(2)=0,则使得
上是减函数,且f(2)=0,则使得![]() 成立的x的取值范围是___________________
成立的x的取值范围是___________________
8.函数![]() 的图像的最高点的坐标是
的图像的最高点的坐标是
9. 对于函数f(x)定义域中任意的x1,x2(x1≠x2),有如下结论:①f(x1+x2)=f(x1)·f(x2)
② f(x1·x2)=f(x1)+f(x2) ③![]() >0 ④
>0 ④![]() .
.
当f(x)=![]() 时,上述结论中正确结论的序号是
______ .
时,上述结论中正确结论的序号是
______ .
10.已知函数![]() (x)=
(x)=![]() .
.![]() ,给出三个命题:①
,给出三个命题:①![]() (x)的值域是
(x)的值域是![]() ;②若
;②若![]() (-2)=
(-2)= ![]() (2),则
(2),则![]() (x)的图象关于y轴对称;③
(x)的图象关于y轴对称;③![]() 至多有两个零点,其中一定正确命题的序号是_______;
至多有两个零点,其中一定正确命题的序号是_______;
二.选择题
11.![]() 和
和![]() 是奇函数,且
是奇函数,且![]() 在
在![]() 上有最大值8,则在
上有最大值8,则在![]() 上
上![]() ( )
( )
A.最小值-8 B.最大值-8 C.最小值-6 D.最小值-4
12.若函数![]() 且
且![]() ,则
,则![]() 的值是
( )
的值是
( )
A. 1 B. -1 C. 2 D. -2
13.已知函数![]() 对任意实数
对任意实数![]() 都有
都有![]() 成立,若当
成立,若当![]() 时,
时,![]() 恒成立,则
恒成立,则![]() 的取值范围是
(
)
的取值范围是
(
)
A.![]() B.
B.![]() C.
C.![]() D.不能确定
D.不能确定
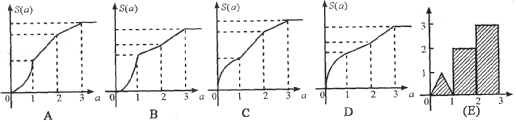
14.图形E(如图)是由底为1,高为1的等腰三角形及高为2和3的二矩形所构成,函数S=S(a)(![]() )是图形E介于平行线y=0及y=a之间的那一部分面积,则函数S(a)的图形大致为
( )
)是图形E介于平行线y=0及y=a之间的那一部分面积,则函数S(a)的图形大致为
( )
 |
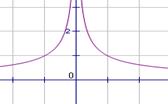
15. 如图,幂函数
 |
16. 当![]() 时,求函数
时,求函数![]() 的最小值并求出取得最小值时
的最小值并求出取得最小值时![]() 的值。
的值。
17.已知定义在![]() 上的函数
上的函数![]() 满足
满足![]() 。且对任意
。且对任意![]() 且
且![]() 都有
都有![]() 成立,解关于
成立,解关于![]() 的不等式:
的不等式: ![]()
18.设函数![]() (x)是定义在
(x)是定义在![]() 上的偶函数,当
上的偶函数,当![]() 时,
时,![]() (x)=
(x)= ![]() ,
,![]()
(1)求![]() (x)的表达式(2)是否存在
(x)的表达式(2)是否存在![]() ,使得当
,使得当![]() 时,
时,![]() (x)有最小值4。若存在求出
(x)有最小值4。若存在求出![]() ;若不存在说明理由
;若不存在说明理由
19. 某商品在30天内每件售价P元与时间x天之间的函数关系式是![]() ,该商品的日销售量Q件与时间x(天)之间的函数关系式是Q=
,该商品的日销售量Q件与时间x(天)之间的函数关系式是Q=![]() (
(![]() ,已知每件商品进价为8元,同时销售该商品每天的劳务费为60元,问30天中哪天利润最大?
,已知每件商品进价为8元,同时销售该商品每天的劳务费为60元,问30天中哪天利润最大?
20.(1)求函数![]()
![]() 的最值以及此时
的最值以及此时![]() 的值。
的值。
(2)求函数![]()
![]() 的最值以及此时
的最值以及此时![]() 的值。
的值。
(3)当![]() 时,研究函数
时,研究函数![]() 的最值,你能得到怎样类似的结论(不必证明)。
的最值,你能得到怎样类似的结论(不必证明)。