高一数学第一学期第二次月考试卷
时间：120分钟 满分：150分 命题：许广铫 校对：张尚
一.选择题：（5×12=60）
1. 设AA1是正方体的一条棱，这个正方体中与AA1平行的棱共有（ ）
A.1 B.2 C.3 D.4
2．下列叙述中正确的是（ ）
A．
B．
C．
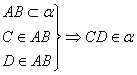D．
3．若一个角的两边分别和另一个角的两边平行，那么这两个角（ ）
A． 相等 B． 互补 C． 相等或互补 D．无法确定
4．在正方体ABCD—A′B′C′D′中，直线AC与直线BC′所成的角为 ( )
A．30° B．60° C． 90° D．45°
5．设有不同的直线a, b和不同的平面
，给出下列四个命题：
①
若
2若
3若
②
④若a⊥b, a⊥
, b⊥
, 则
⊥
. 其中正确的个数是（ ）
A．0； B．1； C．2； D．3；
6．下图所示的是一个立体图形的三视图，请说出立体图形的名称为（ ）
 |
A．圆柱； B．棱锥； C．长方体； D．棱台；
7. 下列说法 不正确 的是 （ ）
A 空间中，一组对边平行且相等的四边形是一定是平行四边形；
B．同一平面的两条垂线一定共面；
C.过直线上一点可以作无数条直线与这条直线垂直，且这些直线都在同一个平面内；
D. 过一条直线有且只有一个平面与已知平面垂直.
8．设
表示直线，
表示平面，则下列命题中 不正确 的是（ ）．
A．
，则
//
B．m // α，α∩β=n 则m // n
C．
,
, 则
D．
,, 则 
9．已知在四面体ABCD中，E、F分别是AC、BD的中点，若CD=2AB=4，
EF
AB，则EF与CD所成的角为（ ）．
A．
B．
C． 
D．
10．正六棱锥的侧棱长为2，底面边长为1，则侧棱与底面所成的角是
A．30° B．45° C．60° D．120°
11．设正四棱锥的高为a,则该四棱锥相邻两侧面组成的二面角大小的取值范围是 ( )
A . （900,1800） B.（600 , 1800 ） C.（600，900 ） D.（450，1800〕
12、正方体的全面积为a,它的顶点都在球面上，则这个球的表面积是：（ ）
A. Πa/3 B. Πa/2 C. 2Πa D. 3Πa .
二．填空（4×6=24）
13．线段AB两端点到平面
的距离都等于2，那么线段AB所在直线与平面的位置关系是
。
14、等体积的球和正方体,它们的表面积的大小关系是
_____
(填”大于、小于或等于”).
15. 已知正方形ABCD的边长为1，AP⊥平面ABCD，且AP=2,
则点P到对角线BD距离＝ ；
16．圆锥的轴截面是边长为a的等边三角形，该圆锥的体积是 ；
17． 以等腰直角三角形ABC斜边BC上的高AD为折痕，
将
ABC折成二面角C—AD—B等于
时，在折成的图形中，ABC为等边三角形。
18. 在侧棱和底面垂直的四棱柱ABCD-A1B1C1D1中，当底面ABCD满足条件
_________时，有
（写出你认为正确的一种条件即可）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
三．解答题。（要求写出必要的证明、计算过程）
19．（12分） 已知：
⊥， //.
求证： ⊥.
20.（12分）如图：已知PA⊥α，PB⊥β，垂足分别为A，B，且α∩β=L。
求证：L⊥平面APB
21．（14分）.求证：如果三个平面两两相交于三条直线，并且其中两条直线平行，那么第三条直线也和它们平行。
22．（14分）将一个边长为a的正方形纸片（如图）剪拼成一个有盖的长方体模型，使长方体的全面积等于原正方形的面积。请你设计一种剪拼方法，用虚线标示在图中，并作简要说明，同时计算出你剪拼的长方体体积。
23、（本题满分14分）
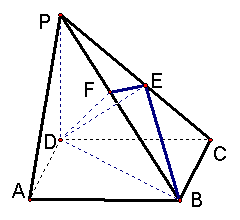
如图，在四棱锥
中，底面ABCD是正方形，侧棱
底面ABCD，
，E是PC的中点，作
交PB于点F。
求证：① 
平面
；
②证明
平面EFD；
③求二面角
的大小。
