普陀区高一第一学期数学期终调研测试卷 2006-1
试卷说明:
1. 本套试卷分两个部分. A卷试题为必做题,B卷试题为选做题.
2. A卷满分100分,B卷满分20分.
3. 本套试卷总测试时间为100分钟.
4. 本卷中的部分试题有新老教材之分,请考生解答相应的试题,否则该题不给分.
A卷
| 题号 | 一 | 二 | 三 | A卷总分 | ||||
| 1—10 | 11—16 | 17 | 18 | 19 | 20 | 21 | | |
| 得分 | | | | | | | | |
![]()
一、填空题(![]() )本大题共有10小题,只要求直接填写结果,每个空格填对得4分,否则一律不给分.
)本大题共有10小题,只要求直接填写结果,每个空格填对得4分,否则一律不给分.
1.命题:“若![]() ,则
,则![]() ”是________命题(填“真”或“假”).
”是________命题(填“真”或“假”).
2.设![]() ,
,![]() ,则
,则![]() .
.
3.函数![]() 的定义域是____
____.
的定义域是____
____.
4.(老教材)计算:![]() =________.
=________.
(新教材)设![]() ,且
,且![]() ,则函数
,则函数![]() 的图像必过的定点坐标是
.
的图像必过的定点坐标是
.
5.设函数![]() ,则
,则![]() .
.
6.设奇函数![]() ,
,![]() ,满足
,满足![]() ,则
,则![]() _______.
_______.
7.函数![]() 的值域为
.
的值域为
.
8. 已知集合![]() ,则
,则![]() .(
.(![]() 表示整数集)
表示整数集)
9.给出下列命题:① 3.14![]() ; ②
; ② ![]() ; ③
; ③ ![]() ;
;
④ ![]() ;⑤
;⑤ ![]() .
.
其中所有正确命题的序号是 .
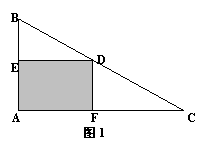 10.
10.![]() 如图1所示,直角边
如图1所示,直角边![]() ,
,![]() .
.![]() 点
点
是斜边BC上的动点,![]() 交于点
交于点![]() ,
,![]() 交于点
交于点![]() .设
.设![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数
的函数![]() .
.
![]() 二、选择题(
二、选择题(![]() )本大题共有6小题,每小题有且仅有一个正确的选项,每题选对得4分,选错或不选均不得分.
)本大题共有6小题,每小题有且仅有一个正确的选项,每题选对得4分,选错或不选均不得分.
11.“![]() ”是“
”是“![]() ”的_________条件
( )
”的_________条件
( )
A.充分非必要; B.必要非充分; C.充要; D.既非充分又非必要.
12.下列关于集合的说法中,正确的是 ( )
A. 绝对值很小的数的全体形成一个集合;
B. 方程![]() 的解集是
的解集是![]() ;
;
C. 集合![]() 和集合
和集合![]() 相等;
相等;
D. 空集是任何集合的真子集.
13.下列函数中,奇函数是 ( )
A.![]() ; B.
; B. ![]() ; C.
; C. ![]() ; D.
; D.![]() .
.
14.(老教材)下面四种说法中,正确的是 ( )
A. 实数![]() ,则
,则![]() 是纯虚数; B. 模相等的复数为共轭复数;
是纯虚数; B. 模相等的复数为共轭复数;
C. 如果z是纯虚数,则![]() ;
D. 任何数的偶次幂不小于零.
;
D. 任何数的偶次幂不小于零.
(新教材)若函数![]() 存在反函数,则方程
存在反函数,则方程![]() (
(![]() 为常数) ( )
为常数) ( )
A. 有且只有一个实根; B. 至少有一个实根; C. 至多有一个实根; D. 没有实数根.
15.函数![]() 在区间
在区间![]() 上是减函数,则
上是减函数,则![]() 的取值范围是 ( )
的取值范围是 ( )
A.![]() ; B.
; B.![]() ; C.
; C.![]() ; D.
; D.![]() .
.
16.已知![]() ,下列给出四个命题,其中假命题是
( )
,下列给出四个命题,其中假命题是
( )
A.若![]() ,则
,则![]() ; B.
若
; B.
若![]() ,则
,则![]() ;
;
C.若![]() ,则
,则![]() ;
D.若
;
D.若![]() ,则
,则![]() .
.
三、简答题(![]() )本大题共有3题,解答下列各题必须写出必要的步骤.
)本大题共有3题,解答下列各题必须写出必要的步骤.
![]() 17.(本题满分6分) 用函数单调性的定义证明:函数
17.(本题满分6分) 用函数单调性的定义证明:函数![]() 在区间
在区间![]() 上为减函数.
上为减函数.
![]() 18.(本题满分6分)
18.(本题满分6分)
求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
![]() 19.(本题满分6分)
19.(本题满分6分)
解不等式:![]() .
.
![]() 四、解答题(
四、解答题(![]() )本大题共有2题,解答下列各题必须写出必要的步骤.
)本大题共有2题,解答下列各题必须写出必要的步骤.
20.(本题满分8分. 老教材试题第1小题4分,第2小题4分;新教材试题第1小题3分,第2小题5分.)
| (老教材) 设 (1)求 (2)在复数范围内求方程的解. | (新教材) 设函数 (1)若 (2)在满足(1)的条件下,解方程: |
21.(本题满分10分,其中第1小题3分,第2小题3分,第3小题4分)
![]()
某商场在促销期间规定:商场内所有商品按标价的80%出售;同时,当顾客在该商场内消费满一定金额后,按如下方案获得相应金额的奖券:
| 消费金额(元)的范围 |
|
|
|
| …… |
| 获得奖券的金额(元) | 28 | 58 | 88 | 128 | …… |
根据上述促销方法,顾客在该商场购物可以获得双重优惠.例如:购买标价为400元的商品,则消费金额为320元,然后还能获得对应的奖券金额为28元. 于是,该顾客获得的优惠额为:![]() 元. 设购买商品得到的优惠率=
元. 设购买商品得到的优惠率=![]() .试问:
.试问:
(1) 购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)
当商品的标价为![]() 元时,试写出顾客得到的优惠率
元时,试写出顾客得到的优惠率![]() 关于标价
关于标价![]() 元之间的函数关系式;
元之间的函数关系式;
(3)
当顾客购买标价不超过600元的商品时,该顾客是否可以得到超过![]() 的优惠率?若可以,请举一例;若不可以,试说明你的理由.
的优惠率?若可以,请举一例;若不可以,试说明你的理由.
B卷
| 题号 | 一 | 三 | 总分 |
| 1~3 | 4 | ||
| 得分 | | | |
![]()
一、填空题(![]() )本大题共有2小题,只要求直接填写结果,每个空格填对得3分,否则一律不给分.
)本大题共有2小题,只要求直接填写结果,每个空格填对得3分,否则一律不给分.
1.已知函数![]() ,函数
,函数![]() ,则方程
,则方程![]() 在实数范围内解的个数为 个.
在实数范围内解的个数为 个.
2.已知函数![]() ,给出以下三个条件:
,给出以下三个条件:
(1) 存在![]() ,使得
,使得![]() ;
;
(2) ![]() 成立;
成立;
(3) ![]() 在区间
在区间![]() 上是增函数.
上是增函数.
若![]() 同时满足条件 和
(填入两个条件的编号),则
同时满足条件 和
(填入两个条件的编号),则![]() 的一个可能的解析式为
的一个可能的解析式为![]() .
.
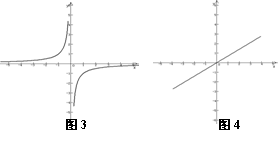
![]() 二、选择题(
二、选择题(![]() )本大题共有1小题,每小题有且仅有一个正确的选项,选对得3分,选错或不选均不得分.
)本大题共有1小题,每小题有且仅有一个正确的选项,选对得3分,选错或不选均不得分.
3.函数![]() 的图像分别如右图3、4所示.函数
的图像分别如右图3、4所示.函数![]() . 则以下有关函数
. 则以下有关函数![]() 的性质中,错误的是( )
的性质中,错误的是( )
A.函数在![]() 处没有意义;
B.函数在定义域内单调递增;
处没有意义;
B.函数在定义域内单调递增;
C.函数![]() 是奇函数;
D.函数没有最大值也没有最小值.
是奇函数;
D.函数没有最大值也没有最小值.
![]() 三、解答题(
三、解答题(![]() )本大题共有1题,解答下列各题必须写出必要的步骤.
)本大题共有1题,解答下列各题必须写出必要的步骤.
4.(本题满分11分,其中第1小题5分,第2小题6分)
设定义域为R的函数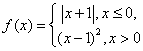 .
.
 (1) 在平面直角坐标系内作出该函数的图像;
(1) 在平面直角坐标系内作出该函数的图像;
(2) 试找出一组![]() 和
和![]() 的值,使得关于
的值,使得关于![]() 的方程
的方程![]() 有7个不同的实根.请说明你的理由.
有7个不同的实根.请说明你的理由.
高一第一学期数学期终调研测试卷参考答案及评分标准 2006-01pt
A卷
一、填空题:
1.假命题 2.![]() 3.
3. ![]() 4. 老教材:
4. 老教材:![]() ;新教材:
;新教材:![]() ; 5. 1 6. -11 7.
; 5. 1 6. -11 7.![]() 8.
8. ![]() 9. ①③⑤ 10.
9. ①③⑤ 10.![]() (注:定义域取闭区间不扣分)
(注:定义域取闭区间不扣分)
二、选择题:
11.A 12.C 13.B 14. 老教材C ; 新教材C 15.C 16.B
三、简答题:
17.证:对任意的![]() ,有
,有
![]()
![]()
所以,函数![]() 在
在![]() 上为减函数.
上为减函数.
18. 解:因为![]()
![]()
因为![]() ,所以当
,所以当![]() 时,函数取得最小值
时,函数取得最小值![]() ;
;
而![]()
![]() ,故由对称性可知当
,故由对称性可知当![]() 时,取到函数的最大值
时,取到函数的最大值![]() .
.
19. 解法一:由不等式![]() ,可知
,可知
(1)
当![]() 时,原不等式即为
时,原不等式即为![]() ;
;
(2)
当![]() 时,原不等式即为
时,原不等式即为![]() 不等式无解.
不等式无解.
综上所述:不等式的解为![]() .
.
解法二:设![]()
![]()
即![]() ,亦即
,亦即![]() ,故不等式的解为
,故不等式的解为![]() .
.
四、解答题:
20. (老教材)解:(1)设方程![]() 的两个虚根为
的两个虚根为![]()
由于该方程为实系数方程,所以方程两根必为共轭虚根,即![]()
又![]()
![]()
![]() .
.
(2)由(1)得方程![]() ,即
,即![]()
解得![]() .
.
20. (新教材)解:(1)据题意![]() 代入
代入![]() ,得
,得
![]() ,所以
,所以![]() .
.
(2)由![]() ,得
,得![]()
所以![]() ,
,![]() .
.
故方程即为![]() ,
,
![]()
![]()
![]() ,解得
,解得![]()
由于, 经检验![]() 都为原方程的根.
都为原方程的根.
21. 解:(1)由题意,标价为1000元的商品消费金额为![]() 元,
元,
故优惠额为![]() 元,则优惠率为
元,则优惠率为![]() .
.
(2)由题意,当消费金额为188元时,其标价为235元;
当消费金额为388元时,其标价为485元;
当消费金额为588元时,其标价为735元.
由此可得,当商品的标价为![]() 元时,顾客得到的优惠率
元时,顾客得到的优惠率![]() 关于标价
关于标价![]() 元之间的函数关系式为
元之间的函数关系式为
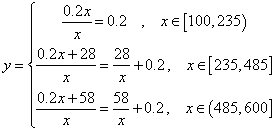
(3)当![]() 时,优惠率即为
时,优惠率即为![]() ;
;
当![]() 时,优惠率为:
时,优惠率为:![]() ,
,
此时的最大优惠率为![]() ;
;
当![]() 时,优惠率为:
时,优惠率为:![]() ,
,
此时的优惠率![]() ;
;
综上, 当顾客购买不超过600元商品时,可得到的优惠率不会超过35%.
B卷
一、填空题
1. 4个; 2. (开放题) 满足条件(1)(2),![]() 等;满足条件(1)(3),
等;满足条件(1)(3),![]() 等;满足条件(2)(3),
等;满足条件(2)(3),![]() 等.
等.
二、选择题
3. B
三、解答题
4. 解:(1)见下图.
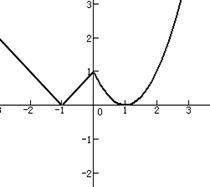 (2)(开放题)如
(2)(开放题)如![]() 等.
等.
设![]() ,由图像可得以上有关于t的方程必须有一解为1,另一解在区间
,由图像可得以上有关于t的方程必须有一解为1,另一解在区间![]() 中,才会使得关于
中,才会使得关于![]() 的方程
的方程![]() 有7个解. 其中,
有7个解. 其中,![]() 有3个解,
有3个解,![]() 有四个解.
有四个解.
所以可令![]() ,即可得方程
,即可得方程![]() .
.