2005－2006学年度上学期
高中学生学科素质训练
高一数学同步测试（4）—映射与函数
说明：本试卷分第I卷和第II卷两部分，第I卷60分，第II卷90分，共150分；答题时间150分钟．
第Ⅰ卷（共60分）
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．
1．函数y=f（x）的图像与直线x=2的公共点共有 （ ）
A．0个 B．1个 C．0个或1个 D．不能确定
2．下表是某小卖部一周卖出热茶的杯数与当天气温的对比表：
| 气温/℃ | 18 | 13 | 10 | 4 | －1 |
| 杯数 | 24 | 34 | 39 | 51 | 63 |
若热茶杯数y与气温x近似地满足线性关系，则其关系式最接近的是 （ ）
A．
B．
C．
D．
3．如果f(a+b)=f(a)•f(b)且f(1)=2，则
+
+
+…+
等于 （ ）
A．1002 B．1003 C．2004 D．2006
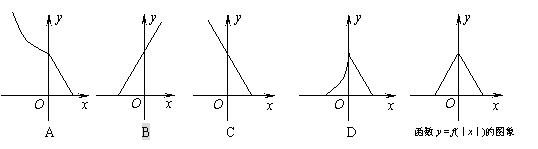4．已知函数y = f(x)的图象如右图所示，则函数y = f(x)的图象不可能 是 （ ）
5．已知映射f:AàB，其中集合A＝{－3，－2，－1，1，2，3，4}，集合B中的元素都是A
中的元素在映射f下的象，且对任意的a∈A，在B中和它对应的元素是a，则集合B中
的元素的个数是 （ ）
A．4 B．5 C．6 D．7
6．设集合A和B都是自然数集合N，映射f：A→B把集合A中的元素n映射到集合B中
的元素2n＋n，则在映射f下，象20的原象是 ( )
A．2 B．3 C．4 D．5
7．已知
的解析式可取为 （ ）
A．
B．
C．
D．
8．在股票买卖过程中，经常用到两种曲线，一种是即时价格曲线y =
(
)，另一种是平均
价格曲线y
=
(如3 =(2)是指开始买卖后2个小时的即时价格为3元 ；3 = g(2)表示
2个小时内的平均价格为3元)．下图给出的四个图像，其中实线表示y=
，虚线表示
y = ，其中可能正确的是
（ ）
9．设函数
，则使得f(x)
1的自变量x的取值范围为 （ ）
A．(-∞,-2)
[0,10] B．(-∞,-2)[0,1] C．(-∞,-2)[1,10] D．[-2,0][1,10]
10．若和g(x)都是定义在实数集R上的函数，且方程
有实数解，则
不可能是 （ ）
A．
B．
C．
D．
11．已知函数f(
＋1)=x＋1，则函数f(x)的解析式为 （ ）
A．f(x)=x2 B．f(x)=x2＋1(x≥1)
C．f(x)=x2－2x＋2(x≥1) D．f(x)=x2－2x(x≥1)
12．某商场宣传在“五一黄金周”期间对顾客购物实行一定的优惠，商场规定：
①如一次性购物不超过200元，不予以折扣；
②如一次性购物超过200元但不超过500元的，按标价给予九折优惠；
③如一次性购物超过500元的，其中500元给予9折优惠，超过500元的部分给予八五折优惠．
某人两次去购物，分别付款176元和432元，如果他只去一次购买同样的商品，则应付
款 （ ）
A．608元 B．574.1元 C．582.6元 D．456.8元
第Ⅱ卷（共90分）
二、填空题：本题共4小题，每小题4分，共16分．把答案填在题中的横线上．
13．已知
则不等式
的解集是
14．设函数
其中
是
的小数点后的第
位数字。例如
则
（共2005个）=___________.
15.不等式
的解集是 . 其中
16. 设函数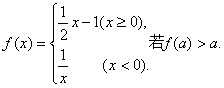
则实数a的取值范围是 .
三、解答题:本大题共6小题，共74分．解答应写出必要的文字说明、证明过程及演算步骤．
17．求下列函数的定义域：（12分）
（1）
;
（2）
.
18．已知
在映射的作用下的像是
，求
在作用下的像和
在作用下的原像. （12分）
19．已知函数
(x)=f(x)＋g(x)，其中f(x)是x的正比例函数，g(x)是x的反比例函数，
且(
)=16，(1)=8.（12分）
（1）求(x)的解析式，并指出定义域； （2）求(x)的值域.
20．已知xy＜0，并且4x
-9y=36．由此能否确定一个函数关系y=f(x)？如果能，求出其解析式、定义域和值域；如果不能，请说明理由．（12分）
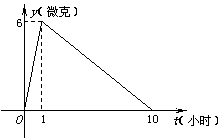
21．某医药研究所开发一种新药，如果成人按规定的剂量服用，据监测：服药后每毫升血液中的含药量
与时间
之间近似满足如图所示的曲线. （12分）
（1）写出服药后与之间的函数关系式；
（2）据测定：每毫升血液中含药量不少于4微克时治疗疾病有效，假若某病人一天中第一次服药时间为早晨
，问一天中怎样安排服药的时间（共4次）效果最佳？
22．如图，两铁路线垂直相交于站A，若已知AB=100公里，甲火车从A站出发，沿AC方向以50公里/小时的速度行驶，同时乙火车以v公里/小时的速度从B站沿BA方向行驶至A站即停止前行（甲车仍继续行驶）. （14分）
（1）用v表示甲、乙两车的最近距离（两车的车长忽略不计）；
|
|
2005－2006学年度上学期
高中学生学科素质训练
高一数学同步测试（4）—映射与函数答案
一、选择题
1．C 2．C. 3．D. 4．B 5．A. 6．C 7．C 8．C 9．C 10．B 11.C 12.C
二、填空题
13.
. 14. 1. 15. （
）∪（0，+∞）. 16. 
.
三、解答题
17.（1）
（2）
18. 在作用下的像是
；在作用下的原像是
19. (1)设f(x)=ax，g(x)=
，a、b为比例常数，则(x)=f(x)＋g(x)=ax＋
由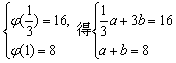
，解得
∴(x)=3x＋
，其定义域为(－∞，0)∪(0，＋∞)
(2)由y =3x＋，得3x2－yx＋5=0(x≠0)
∵x∈R且x≠0，∴Δ=y2－60≥0，∴y≥2
或y≤－2
∴(x) 的值域为(－∞，－2
∪［2，＋∞
20．解：
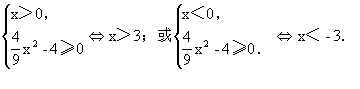
所以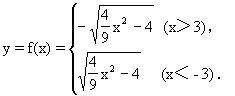
因此能确定一个函数关系y=f(x)．其定义域为(-∞，-3)∪(3，+∞)．且不难得到其值域为(-∞，0)∪(0，＋∞)．
21．(1)依题得，
(2)设第二次服药时在第一次服药后t1小时，则
,因而第二次服药应在11:00；
设第三次服药在第一次服药后t2小时，则此时血液中含药量应为两次服药量的和，即有
解得t2=9小时，故第三次服药应在16:00；
设第四次服药在第一次后t3小时（t3>10），则此时第一次服进的药已吸收完，此时血液中含药量应为第二、三次的和，
解得t3=13.5小时，故第四次服药应在20:30.
22．（1）设乙车行驶t小时到D，甲车行驶t小时到E，1°若0≤tV≤100，
则DE2=AE2+AD2=(100－tV)2+(50t)2=(2500+V2)t2－200Vt+10000
当t=
时，DE2取最小值，DE也取最小值，其最小值为
2°若tV>100时，乙车停止，甲车继续前行DE越来越大，无最大值.
由1°、2°知，甲、乙两车的最近距离为公里
（2）t0==
当且仅当V=
即V=50公里/小时时，t0最大.
答：v=50/小时时，t0最大.