高一数学同步测试（9）—对数与对数函数（附答案）江苏教育版

2004－2005学年度上学期

高一数学同步测试（9）—对数与对数函数

一、选择题：

1．的值是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

A．　　　　　　　　　　　 B．1　　　　　　　　　　　 C．　　　　　　　　　　 D．2

2．若log₂=0，则x、y、z的大小关系是　　　　　　　　　　 　（　　）

A．z＜x＜y　　　　　　　 B．x＜y＜z　　　　　　　 C．y＜z＜x　　　　　　　 D．z＜y＜x

3．已知x=+1,则log₄(x³－x－6)等于　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

A.　　　　　　　　　　　　B.　　　　　　　　　　　　C.0　　　　　　　　　　　　　　D.

　　　 4．已知lg2=a，lg3=b，则等于　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

A．　　　　　 B．　　　　 C．　　　　　 D．

5．已知2 lg(x－2y)=lgx＋lgy，则的值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　A．1　　　 　　　　　　B．4　　　　 　　　　 C．1或4　　　　 　D．4 或　

6.函数y=的定义域为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

A．(，＋∞)　　　　 B．［1，＋∞　　　　C．( ，1　　　　　 D．(－∞，1)

7．已知函数y=log (ax²＋2x＋1)的值域为R，则实数a的取值范围是　　　　　　　　　 （　　）

　　 A．a ＞ 1　　　　　 B．0≤a＜ 1　　 　 C．0＜a＜1　　　　　 D．0≤a≤1　　

8.已知f(e^x)=x，则f(5)等于　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　A．e⁵B．5^e C．ln5　　　　　　D．log₅e

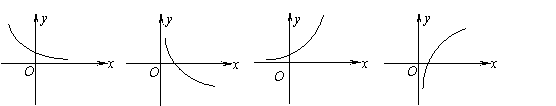9．若的图像是　 　　　　　　　　　　 （　　）

A　　　　　　　　 B　　　　　　　　 C　　　　　　　　 D

10．若在区间上是增函数，则的取值范围是（　　）

A． 　　 B．　　 C．　　　 D．

11．设集合等于　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　　　　　　　　　　　　　B．

　　　 C．　　　　　　　　　　　　　　　　　　　　　D．

12．函数的反函数为　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　 B．

C．　　　　　　　　　　 D．

二、填空题：

13．计算：log_2.56.25＋lg＋ln＋= 　　　　　　　　　　　　 ．

14．函数y=log₄(x－1)²(x＜1＝的反函数为___　　 　　　　　　　　　_______．

15．已知m＞1，试比较(lgm)^0.9与(lgm)^0.8的大小　　　　　　　　　　　　  ．

16．函数y =(logx)²－logx²＋5 在 2≤x≤4时的值域为_____　　　　 _　　　　  ．

三、解答题：

17．已知y=log_a(2－ax)在区间{0，1}上是x的减函数，求a的取值范围．

 

18．已知函数f(x)=lg[(a²－1)x²＋(a＋1)x＋1]，若f(x)的定义域为R，求实数a的取值范围．

 

19．已知f(x)=x²＋(lga＋2)x＋lgb，f(－1)=－2，当x∈R时f(x)≥2x恒成立，求实数a的值，并求此时f(x)的最小值？

 

20．设0＜x＜1，a＞0且a≠1，试比较log_a(1－x)与log_a(1＋x)的大小．

 

21．已知函数f(x)=log_a(a－a^x)且a＞1，

（1）求函数的定义域和值域；

（2）讨论f(x)在其定义域上的单调性；

（3）证明函数图象关于y=x对称．

 

22．在对数函数y=log₂x的图象上(如图)，有A、B、C三点，它们的横坐标依次为a、a＋1、a＋2，其中a≥1，求△ABC面积的最大值．

　　　　　　　　　　　　　　　　　　　　　　　　　　 

 

参考答案

一、选择题： ADBCB　CDCBA　AB

二、填空题：13.，14.y=1－2^x(x∈R)， 15. (lgm)^0.9≤(lgm)^0.8，16.

三、解答题：

17.解析：先求函数定义域：由2－ax＞0，得ax＜2

又a是对数的底数，

∴a＞0且a≠1，∴x＜

由递减区间[0，1]应在定义域内可得＞1，∴a＜2

又2－ax在x∈[0，1]是减函数

∴y=log_a(2－ax)在区间[0，1]也是减函数，由复合函数单调性可知：a＞1

∴1＜a＜2

18、解：依题意(a²－1)x²＋(a＋1)x＋1＞0对一切x∈R恒成立．

当a²－1≠0时，其充要条件是：

解得a＜－1或a＞

又a=－1，f(x)=0满足题意，a=1，不合题意．

所以a的取值范围是：(－∞，－1]∪(，＋∞)

19、解析：由f(－1)=－2 ，得：f(－1)=1－(lga＋2)＋lgb=－2，解之lga－lgb=1，

∴=10，a=10b．

又由x∈R，f(x)≥2x恒成立．知：x²＋(lga＋2)x＋lgb≥2x，即x²＋xlga＋lgb≥0，对x∈R恒成立，

由Δ=lg²a－4lgb≤0，整理得(1＋lgb)²－4lgb≤0

即(lgb－1)²≤0，只有lgb=1，不等式成立．

即b=10，∴a=100．

∴f(x)=x²＋4x＋1=(2＋x)²－3

当x=－2时，f(x) _min=－3．

20.解法一：作差法

log_a(1－x)－log_a(1＋x)= －=(lg(1－x)－lg(1＋x))

∵0＜x＜1，∴0＜1－x＜1＜1＋x

∴上式=－[(lg(1－x)＋lg(1＋x)]=－·lg(1－x²)

由0＜x＜1，得，lg(1－x²)＜0，∴－·lg(1－x²)＞0，

∴log_a(1－x)＞log_a(1＋x)

解法二：作商法

=log_(1－x)(1＋x)

∵0＜x＜1，∴0＜1－x＜1＋x，∴log_(1－x)(1＋x)=－log_(1－x)(1＋x)=log_(1－x)

由0＜x＜1，∴1＋x＞1，0＜1－x²＜1

∴0＜(1－x)(1＋x)＜1，∴＞1－x＞0

∴0＜log_(1－x) ＜log_(1－x)(1－x)=1

∴log_a(1－x)＞log_a(1＋x)

解法三：平方后比较大小

∵log_a²(1－x)－log_a²(1＋x)=[log_a(1－x)＋log_a(1＋x)][log_a(1－x)－log_a(1＋x)]

=log_a(1－x²)·log_a=·lg(1－x²)·lg

∵0＜x＜1，∴0＜1－x²＜1，0＜＜1

∴lg(1－x²)＜0，lg＜0

∴log_a²(1－x)＞log_a²(1＋x)，即log_a(1－x)＞log_a(1＋x)

解法四：分类讨论去掉绝对值

当a＞1时，log_a(1－x)－log_a(1＋x)=－log_a(1－x)－log_a(1＋x)=－log_a(1－x²)

∵0＜1－x＜1＜1＋x，∴0＜1－x²＜1

∴log_a(1－x²)＜0，∴－log_a(1－x²)＞0

当0＜a＜1时，由0＜x＜1，则有log_a(1－x)＞0，log_a(1＋x)＜0

∴log_a(1－x)－log_a(1＋x)=log_a(1－x)＋log_a(1＋x)=log_a(1－x²)＞0

∴当a＞0且a≠1时，总有log_a(1－x)＞log_a(1＋x)

21.解析：(1)定义域为(－∞，1)，值域为(－∞，1)

(2)设1＞x₂＞x₁

∵a＞1，∴，于是a－＜a－

则log_a(a－a)＜log_a(a－)

即f(x₂)＜f(x₁)

∴f(x)在定义域(－∞，1)上是减函数

(3)证明：令y=log_a(a－a^x)(x＜1)，则a－a^x=a^y，x=log_a(a－a^y)

∴f^－1(x)=log_a(a－a^x)(x＜1)

故f(x)的反函数是其自身，得函数f(x)=log_a(a－a^x)(x＜1＝图象关于y=x对称．

22.

解析：根据已知条件，A、B、C三点坐标分别为(a，log₂a)，(a＋1，log₂(a＋1))，(a＋2，log₂(a＋2))，则△ABC的面积

S=

因为,所以