|
高一数学期考试卷【Ⅰ】 2002,1,27
班级____座号____姓名_________
〖试卷说明〗:本试卷满分共100分,有22个小题,考试时间120分钟;
本试卷共3张(6面),试卷(Ⅰ)是问卷,试卷(Ⅱ)(Ⅲ)是答卷,考试结束只要交试卷(Ⅱ)(Ⅲ),试卷分三个大题,请将一、二大题的解答填在答卷上;
一、选择题:本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
设集合![]() ,则
,则
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.
下列四组函数中,表示同一个函数的是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.
下列函数中,在![]() 上为减函数的是
上为减函数的是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.
在正项等比数列![]() 中,
中,![]() ,那么数列
,那么数列![]() 的通项公式为
的通项公式为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.
已知角![]() 的终边经过点
的终边经过点![]() ,则
,则![]() 的正弦值为
的正弦值为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.
若![]() ,则
,则![]() 是
是
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
7.
在等差数列![]() 中,已知
中,已知![]() 设
设![]() 则
则![]() 等于
等于
A.8 B.9
C.10 D.11
8.
![]() 成等比数列的充分而不必要条件是
成等比数列的充分而不必要条件是
A.![]() 成等差数列 B.
成等差数列 B.![]()
C.![]() 成等比数列 D.
成等比数列 D.![]()
9.

 |
已知函数
A.①②④③ B.①②③④
C.④③②① D.④③①②
10.
计算机是将信息转换成二进制进行处理的,二进制即“逢2进1”,如(1101)2表示二进制数,将它转换成十进制形式是1×23+1×22+0×21+1×20=13,那么将二进制数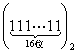 转换成十进制形式是
转换成十进制形式是
A.217-2 B.216-2 C.216-1 D.215-1
二、填空题:本大题共6小题,每小题3分,共18分,把答案填在题中横线上.
11.
不等式![]() 的解集为_________________________________________;
的解集为_________________________________________;
12.
数列![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…的一个通项公式为
,…的一个通项公式为![]() _________________;
_________________;
13.
函数![]() 的单调递增区间为___________________________;
的单调递增区间为___________________________;
14.
已知![]() ,则
,则![]() 的值为_________________;
的值为_________________;
15.
已知函数![]() ,如果
,如果![]() 的等差中项为
的等差中项为![]() ,那么常数
,那么常数![]() 的值为__________________________;
的值为__________________________;
16.
老师在黑板上按顺序写了4个数构成一个数列,四个学生各指出这个数列的一个特征:
张三说:前3项成等差数列;
李四说:后3项成等比数列;
王五说:4个数的和为24;
马六说:4个数的积为24;
如果其中恰有三人说得正确,请写出一个这样的数列__________________________;
|
高一数学期考试卷【Ⅱ】 2002,1,27
班级____座号____姓名_________
本试卷满分共100分,有22个小题,考试时间120分钟.
| 题号 | 一 | 二 | 17 | 18 | 19 | 20 | 21 | 22 | 总分 |
| 得分 |
一. 选择题:本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的,将您认为正确选项填在表格的相应位置;
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
二. 填空题:本大题共6小题,每小题3分,共18分,将答案填在表格的相应位置;
| 11 | 14 | ||
| 12 | 15 | ||
| 13 | 16 |
三. 解答题:本大题共6小题,共52分,解答应写出文字说明、证明过程或演算步骤.
17.
(6分)化简:![]()
18.
(8分)已知点![]() 即在函数
即在函数![]() 的图象上,又在其反函数图象上;
的图象上,又在其反函数图象上;
(1)求![]() ;
;
(2)判断![]() 在其定义域上的单调性,并用定义法证明;
在其定义域上的单调性,并用定义法证明;
19.
(8分)数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() 对任意
对任意![]() 成立;
成立;
(1)求![]() ;
;
(2)求数列![]() 的通项公式;
的通项公式;
高一数学期考试卷【Ⅲ】
班级____座号____姓名_________
20.
(12分)已知函数![]() ,
,![]() 且
且![]()
(1)求函数![]() 的定义域;
的定义域;
(2)判断![]() 的奇偶性,并予以证明;
的奇偶性,并予以证明;
(3)当![]() 时,求使
时,求使![]() 的x取值范围。
的x取值范围。
21.
(10分)在公差不为零的等差数列![]() 和等比数列
和等比数列![]() 中,已知
中,已知![]() ,
,![]() ;
;
(1)求![]() 的公差
的公差![]() 和
和![]() 的公比
的公比![]() ;
;
(2)设![]() +2,求数列
+2,求数列![]() 的通项公式及前
的通项公式及前![]() 项和
项和![]() ;
;
22.
 (8分)根据信息产业部、国家计委、财政部《关于电信资费结构性调整的通知》和福建省邮电管理局、福建省物价局相关文件通知,福州市因特网业务资费(以下称上网资费)自2001年1月21日起执行新标准。
(8分)根据信息产业部、国家计委、财政部《关于电信资费结构性调整的通知》和福建省邮电管理局、福建省物价局相关文件通知,福州市因特网业务资费(以下称上网资费)自2001年1月21日起执行新标准。
某用户在家使用163专线上网,每月上网资费用![]() (元)表示,在单位使用宽带IP上网,每月上网资费用
(元)表示,在单位使用宽带IP上网,每月上网资费用![]() (元)表示,根据新标准,得到上网资费和使用时间
(元)表示,根据新标准,得到上网资费和使用时间![]() (小时)之间的函数关系图;(如右图,每月以30天,即720小时计算)
(小时)之间的函数关系图;(如右图,每月以30天,即720小时计算)
(1)写出![]() 的函数表达式;
的函数表达式;
(2)该用户用哪种方式上网,上网资费更少?