高一(上)数学单元同步练习及期末试题(四)
(第四单元 指数与指数函数)
[重点难点]
1. 理解分数指数的概念;掌握有理指数幂的运算性质;
2. 掌握指数函数的概念:了解指数函数中的自变量x为什么可以取任意实数,能解释为什么。指数函数y=ax中,必须规定底数a要满足a![]() 0且a
0且a![]() 1两个条件,并能熟记这两个条件。
1两个条件,并能熟记这两个条件。
3. 掌握指数函数的图象:能用描点法画出指出函数y=ax在a>1和0<a<1两种情况下的图像;能根据图像说明指数函数的值域为(0,+![]() )。
)。
4.掌握指数函数的性质:在指数函数的底数0<a<1或a>1两种情况下,归纳出指数函数的一些重要性质;能利用指数函数的单调性,比较某些函数值的大小。
一、选择题
1.化简(1+2![]() )(1+2
)(1+2![]() )(1+2
)(1+2![]() )(1+2-
)(1+2-![]() )(1+2
)(1+2![]() ),结果是( )
),结果是( )
(A)![]() (1-2
(1-2![]() )-1 (B)(1-2
)-1 (B)(1-2![]() )-1
)-1
(C)1-2![]() (D)
(D)![]() (1-2
(1-2![]() )
)
2.(![]() )4(
)4(![]() )4等于( )
)4等于( )
(A)a16 (B)a8 (C)a4 (D)a2
3.若a>1,b<0,且ab+a-b=2![]() ,则ab-a-b的值等于( )
,则ab-a-b的值等于( )
(A)![]()
![]() (B)
(B)![]() 2 (C)-2 (D)2
2 (C)-2 (D)2
4.函数f(x)=(a2-1)x在R上是减函数,则a的取值范围是( )
(A)![]() (B)
(B)![]() (C)a<
(C)a<![]() (D)1<
(D)1<![]()
5.下列函数式中,满足f(x+1)=![]() f(x)的是( )
f(x)的是( )
(A) ![]() (x+1) (B)x+
(x+1) (B)x+![]() (C)2x
(D)2-x
(C)2x
(D)2-x
6.下列f(x)=(1+ax)2![]() 是( )
是( )
(A)奇函数 (B)偶函数
(C)非奇非偶函数 (D)既奇且偶函数
7.已知a>b,ab![]() 下列不等式(1)a2>b2,(2)2a>2b,(3)
下列不等式(1)a2>b2,(2)2a>2b,(3)![]() ,(4)a
,(4)a![]() >b
>b![]() ,(5)(
,(5)(![]() )a<(
)a<(![]() )b
)b
中恒成立的有( )
(A)1个 (B)2个 (C)3个 (D)4个
8.函数y=![]() 是( )
是( )
(A)奇函数 (B)偶函数
(C)既奇又偶函数 (D)非奇非偶函数
9.函数y=![]() 的值域是( )
的值域是( )
(A)(-![]() ) (B)(-
) (B)(-![]() 0)
0)![]() (0,+
(0,+![]() )
)
(C)(-1,+![]() )
(D)(-
)
(D)(-![]() ,-1)
,-1)![]() (0,+
(0,+![]() )
)
10.下列函数中,值域为R+的是( )
(A)y=5![]() (B)y=(
(B)y=(![]() )1-x
)1-x
(C)y=![]() (D)y=
(D)y=![]()
11.函数y=![]() 的反函数是( )
的反函数是( )
(A)奇函数且在R+上是减函数 (B)偶函数且在R+上是减函数
(C)奇函数且在R+上是增函数 (D)偶函数且在R+上是增函数
12.下列关系中正确的是( )
(A)(![]() )
)![]() <(
<(![]() )
)![]() <(
<(![]() )
)![]() (B)(
(B)(![]() )
)![]() <(
<(![]() )
)![]() <(
<(![]() )
)![]()
(C)(![]() )
)![]() <(
<(![]() )
)![]() <(
<(![]() )
)![]() (D)(
(D)(![]() )
)![]() <(
<(![]() )
)![]() <(
<(![]() )
)![]()
13.若函数y=3+2x-1的反函数的图像经过P点,则P点坐标是( )
(A)(2,5) (B)(1,3) (C)(5,2) (D)(3,1)
14.函数f(x)=3x+5,则f-1(x)的定义域是( )
(A)(0,+![]() ) (B)(5,+
) (B)(5,+![]() )
)
(C)(6,+![]() ) (D)(-
) (D)(-![]() ,+
,+![]() )
)
15.若方程ax-x-a=0有两个根,则a的取值范围是( )
(A)(1,+![]() ) (B)(0,1)
(C)(0,+
) (B)(0,1)
(C)(0,+![]() ) (D)
) (D)![]()
16.已知函数f(x)=ax+k,它的图像经过点(1,7),又知其反函数的图像经过点(4,0),则函数f(x)的表达式是( )
(A)f(x)=2x+5 (B)f(x)=5x+3 (C)f(x)=3x+4 (D)f(x)=4x+3
17.已知三个实数a,b=aa,c=a![]() ,其中0.9<a<1,则这三个数之间的大小关系是( )
,其中0.9<a<1,则这三个数之间的大小关系是( )
(A)a<c<b (B)a<b<c (C)b<a<c (D)c<a<b
18.已知0<a<1,b<-1,则函数y=ax+b的图像必定不经过( )
(A)第一象限 (B)第二象限
(C)第三象限 (D)第四象限
19.F(x)=(1+![]() 是偶函数,且f(x)不恒等于零,则f(x)( )
是偶函数,且f(x)不恒等于零,则f(x)( )
(A)是奇函数 (B)可能是奇函数,也可能是偶函数
(C)是偶函数 (D)不是奇函数,也不是偶函数
20.一批设备价值a万元,由于使用磨损,每年比上一年价值降低b%,则n年后这批设备的价值为( )
(A)na(1-b%) (B)a(1-nb%) (C)a[(1-(b%))n (D)a(1-b%)n
二、填空题
1.若a![]() <a
<a![]() ,则a的取值范围是
。
,则a的取值范围是
。
2.若10x=3,10y=4,则10x-y= 。
3.化简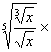
![]() ×
×![]() =
。
=
。
4.函数y=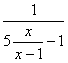 的定义域是
。
的定义域是
。
5.函数y=(![]() )
)![]() (-3
(-3![]() )的值域是 。
)的值域是 。
6.直线x=a(a>0)与函数y=(![]() )x,y=(
)x,y=(![]() )x,y=2x,y=10x的图像依次交于A、B、C、D四点,则这四点从上到下的排列次序是
。
)x,y=2x,y=10x的图像依次交于A、B、C、D四点,则这四点从上到下的排列次序是
。
7.函数y=3![]() 的单调递减区间是
。
的单调递减区间是
。
8.若f(52x-1)=x-2,则f(125)= .
9.函数y=m2x+2mx-1(m>0且m![]() 1),在区间[-1,1]上的最大值是14,则m的值是 .
1),在区间[-1,1]上的最大值是14,则m的值是 .
10.已知f(x)=2x,g(x)是一次函数,记F(x)=f[g(x)],并且点(2,![]() )既在函数F(x)的图像上,又在F-1(x)的图像上,则F(x)的解析式为 .
)既在函数F(x)的图像上,又在F-1(x)的图像上,则F(x)的解析式为 .
三、解答题
1. 设0<a<1,解关于x的不等式a![]() >a
>a![]() 。
。
2. 设f(x)=2x,g(x)=4x,g[g(x)]>g[f(x)]>f[g(x)],求x的取值范围。
3. 已知x![]() [-3,2],求f(x)=
[-3,2],求f(x)=![]() 的最小值与最大值。
的最小值与最大值。
4. 设a![]() R,f(x)=
R,f(x)= ![]() ,试确定a的值,使f(x)为奇函数。
,试确定a的值,使f(x)为奇函数。
5. 已知函数y=(![]() )
)![]() ,求其单调区间及值域。
,求其单调区间及值域。
6. 若函数y=4x-3·2x+3的值域为[1,7],试确定x的取值范围。
7. 若关于x的方程4x+2x·a+a+a=0有实数根,求实数a的取值范围。
8. 已知函数f(x)=![]() ,
,
(1)判断函数的奇偶性;
(2)求该函数的值域;
(3)证明f(x)是R上的增函数。
第四单元 指数与指数函数
一、 选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | C | D | D | D | B | C | A | D | B |
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 答案 | C | D | C | B | A | D | A | A | A | D |
二、填空题
1.0<a<1 2.![]() 3.1
3.1
4.(-![]() ,0)
,0)![]() (0,1)
(0,1) ![]() (1,+
(1,+ ![]() )
) 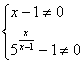 ,联立解得x
,联立解得x![]() 0,且x
0,且x![]() 1。
1。
5.[(![]() )9,39] 令U=-2x2-8x+1=-2(x+2)2+9,∵ -3
)9,39] 令U=-2x2-8x+1=-2(x+2)2+9,∵ -3![]() ,又∵y=(
,又∵y=(![]() )U为减函数,∴(
)U为减函数,∴(![]() )9
)9![]() y
y![]() 39。 6。D、C、B、A。
39。 6。D、C、B、A。
7.(0,+![]() )
)
令y=3U,U=2-3x2,
∵y=3U为增函数,∴y=3![]() 的单调递减区间为[0,+
的单调递减区间为[0,+![]() )。
)。
8.0 f(125)=f(53)=f(52×2-1)=2-2=0。
9.![]() 或3。
或3。
Y=m2x+2mx-1=(mx+1)2-2,
∵它在区间[-1,1]上的最大值是14,∴(m-1+1)2-2=14或(m+1)2-2=14,解得m=![]() 或3。
或3。
10.2![]()
11.∵ g(x)是一次函数,∴可设g(x)=kx+b(k![]() 0), ∵F(x)=f[g(x)]=2kx+b。由已知有F(2)=
0), ∵F(x)=f[g(x)]=2kx+b。由已知有F(2)=![]() ,F(
,F(![]() )=2,∴
)=2,∴  ,∴ k=-
,∴ k=-![]() ,b=
,b=![]() ,∴f(x)=2-
,∴f(x)=2-![]()
三、解答题
1.∵0<a<2,∴
y=ax在(-![]() ,+
,+![]() )上为减函数,∵ a
)上为减函数,∵ a![]() >a
>a![]() , ∴2x2-3x+1<x2+2x-5,解得2<x<3,
, ∴2x2-3x+1<x2+2x-5,解得2<x<3,
2.g[g(x)]=4![]() =4
=4![]() =2
=2![]() ,f[g(x)]=4
,f[g(x)]=4![]() =2
=2![]() ,∵g[g(x)]>g[f(x)]>f[g(x)],
∴2
,∵g[g(x)]>g[f(x)]>f[g(x)],
∴2![]() >2
>2![]() >2
>2![]() ,∴22x+1>2x+1>22x,
∴2x+1>x+1>2x,解得0<x<1
,∴22x+1>2x+1>22x,
∴2x+1>x+1>2x,解得0<x<1
3.f(x)=![]() , ∵x
, ∵x![]() [-3,2], ∴
[-3,2], ∴![]() .则当2-x=
.则当2-x=![]() ,即x=1时,f(x)有最小值
,即x=1时,f(x)有最小值![]() ;当2-x=8,即x=-3时,f(x)有最大值57。
;当2-x=8,即x=-3时,f(x)有最大值57。
4.要使f(x)为奇函数,∵ x![]() R,∴需f(x)+f(-x)=0, ∴f(x)=a-
R,∴需f(x)+f(-x)=0, ∴f(x)=a-![]() =a-
=a-![]() ,由a-
,由a-![]() =0,得2a-
=0,得2a-![]() =0,得2a-
=0,得2a-![]() 。
。
5.令y=(![]() )U,U=x2+2x+5,则y是关于U的减函数,而U是(-
)U,U=x2+2x+5,则y是关于U的减函数,而U是(-![]() ,-1)上的减函数,[-1,+
,-1)上的减函数,[-1,+![]() ]上的增函数,∴ y=(
]上的增函数,∴ y=(![]() )
)![]() 在(-
在(-![]() ,-1)上是增函数,而在[-1,+
,-1)上是增函数,而在[-1,+![]() ]上是减函数,又∵U=x2+2x+5=(x+1)2+4
]上是减函数,又∵U=x2+2x+5=(x+1)2+4![]() 4, ∴y=(
4, ∴y=(![]() )
)![]() 的值域为(0,(
的值域为(0,(![]() )4)]。
)4)]。
6.Y=4x-3![]() ,依题意有
,依题意有
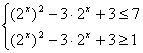 即
即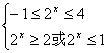 ,∴ 2
,∴ 2![]()
由函数y=2x的单调性可得x![]() 。
。
7.(2x)2+a(2x)+a+1=0有实根,∵ 2x>0,∴相当于t2+at+a+1=0有正根,
则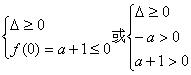
8.(1)∵定义域为x![]() ,且f(-x)=
,且f(-x)=![]() 是奇函数;
是奇函数;
(2)f(x)=![]() 即f(x)的值域为(-1,1);
即f(x)的值域为(-1,1);
(3)设x1,x2![]() ,且x1<x2,f(x1)-f(x2)=
,且x1<x2,f(x1)-f(x2)=![]() (∵分母大于零,且a
(∵分母大于零,且a![]() <a
<a![]() ) ∴f(x)是R上的增函数。
) ∴f(x)是R上的增函数。
9. 已知函数y=(![]() )x2+2x+5,求其单调区间及值域。幕式试确定x的取值范围。
)x2+2x+5,求其单调区间及值域。幕式试确定x的取值范围。![]()