惠州一中高一数学必修2立体几何测试题
试卷满分：150分 考试时间：120分钟
班级___________ 姓名__________ 学号_________ 分数___________
第Ⅰ卷
一、选择题（每小题5分，共60分）
1、线段
在平面
内，则直线与平面的位置关系是
A、
B、
C、由线段的长短而定 D、以上都不对
2、下列说法正确的是
A、三点确定一个平面 B、四边形一定是平面图形
C、梯形一定是平面图形
D、平面和平面
有不同在一条直线上的三个交点
3、垂直于同一条直线的两条直线一定
A、平行 B、相交 C、异面 D、以上都有可能
4、在正方体
中，下列几种说法正确的是
A、
B、
C、
与
成
角 D、
与
成
角
5、若直线
平面，直线
，则
与
的位置关系是
A、
B、与异面 C、与相交
D、与没有公共点
6、下列命题中：（1）、平行于同一直线的两个平面平行；（2）、平行于同一平面的两个平面平行；（3）、垂直于同一直线的两直线平行；（4）、垂直于同一平面的两直线平行.其中正确的个数有
A、1 B、2 C、3 D、4
7、在空间四边形
各边
上分别取
四点，如果与
能相交于点
，那么
A、点必在直线
上 B、点必在直线BD上
C、点必在平面
内
D、点必在平面外
8、a，b，c表示直线，M表示平面，给出下列四个命题：①若a∥M，b∥M，则a∥b；②若b
M，
a∥b，则a∥M；③若a⊥c，b⊥c，则a∥b；④若a⊥M，b⊥M，则a∥b.其中正确命题的个数有
A、0个 B、1个 C、2个 D、3个
9、一个棱柱是正四棱柱的条件是
A、底面是正方形，有两个侧面是矩形 B、底面是正方形，有两个侧面垂直于底面
C、底面是菱形，且有一个顶点处的三条棱两两垂直 D、每个侧面都是全等矩形的四棱柱
10、在棱长为1的正方体上，分别用过共顶点的三条棱中点的平面截该正方体,则截去8个三棱锥后,剩下的凸多面体的体积是
A、
B、
C、
D、
11、已知二面角
的平面角是锐角
，内一点
到的距离为3，点C到棱的距离为4，那么
的值等于
A、
B、
C、
D、
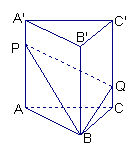
12、如图:直三棱柱ABC—A1B1C1的体积为V，点P、Q分别在侧棱AA1和
CC1上，AP=C1Q，则四棱锥B—APQC的体积为
A、
B、
C、
D、
二、填空题（每小题4分，共16分）
13、等体积的球和正方体,它们的表面积的大小关系是
_____
(填”大于、小于或等于”).
14、正方体中，平面
和平面
的位置关系为
15、已知
垂直平行四边形所在平面，若
，平行则四边形一定是
.
16、如图，在直四棱柱A1B1C1 D1－ABCD中，当底面四边形ABCD满足条件_________时，有A1 B⊥B1 D1．(注：填上你认为正确的一种条件即可，不必考虑所有可能的情形.)
第Ⅱ卷
一、选择题（每小题5分，共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题（每小题4分，共16分）
13、 14、 15、 16、
三、解答题(共74分,要求写出主要的证明、解答过程)
17、已知圆台的上下底面半径分别是2、5,且侧面面积等于两底面面积之和,求该圆台的母线长.
(10分)
18、已知E、F、G、H为空间四边形ABCD的边AB、BC、CD、DA上的点，且ＥＨ∥ＦＧ．
求证：EH∥BD. (12分)
19、已知
中
，
面，
，求证：
面
．(12分)
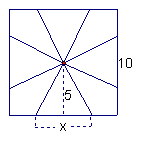
20、一块边长为10
的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,试建立容器的容积
与
的函数关系式,并求出函数的定义域. (12分)
21、已知正方体，
是底对角线的交点.
求证：（１）
面；
（2
）
面．
(14分)
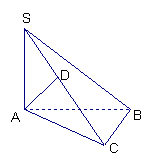
22、已知△BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，
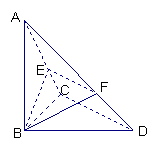∠ADB=60°，E、F分别是AC、AD上的动点，且
（Ⅰ）求证：不论λ为何值，总有平面BEF⊥平面ABC；
（Ⅱ）当λ为何值时，平面BEF⊥平面ACD？ (14分)
高一数学必修2立体几何测试题参考答案
一、选择题（每小题5分，共60分）
ACDDD BCBDD DB
二、填空题（每小题4分，共16分）
13、
14、
15、
16、
三、解答题（共74分,要求写出主要的证明、解答过程）
17、解:设圆台的母线长为
,则
1分
圆台的上底面面积为
3分
圆台的上底面面积为
5分
所以圆台的底面面积为
6分
又圆台的侧面积
8分
于是
9分
即
为所求.
10分
18、证明：
面
，
面
面
6分
又
面，面
面
，
12分
19、证明：
1分
又
面
4分
面
7分
10分
又
面
12分
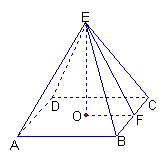
20、解:如图,设所截等腰三角形的底边边长为
.
在
中,
,
3分
所以
, 6分
于是
10分
依题意函数的定义域为
12分
21、证明：（1）连结
，设
连结
，
是正方体 
是平行四边形
且 
2分
又
分别是
的中点，
且
是平行四边形
4分
面
，
面
面
6分
（2）
面
7分
又
， 
9分
11分
同理可证
，
12分
又
面
14分
22、证明：（Ⅰ）∵AB⊥平面BCD， ∴AB⊥CD，
∵CD⊥BC且AB∩BC=B， ∴CD⊥平面ABC. 3分
又
∴不论λ为何值，恒有EF∥CD，∴EF⊥平面ABC，EF平面BEF,
∴不论λ为何值恒有平面BEF⊥平面ABC. 6分
（Ⅱ）由（Ⅰ）知，BE⊥EF，又平面BEF⊥平面ACD，
∴BE⊥平面ACD，∴BE⊥AC. 9分
∵BC=CD=1，∠BCD=90°，∠ADB=60°，
∴
11分
由AB2=AE·AC 得
13分
故当
时，平面BEF⊥平面ACD.
14分