必修5试题江苏教育版

高一数学试卷（必修5第1、3章）

一、选择题(每题5分，合计50分)

1、已知a、b∈（0，1）且ab，则下列各式中最大的是　 （　）

A、a²+b ² 　 B、2　　  C、2ab　　D、a+b

2、在锐角三角形中，下面答案对的是　 （　）

A、sinA ＞ cosB　　 B、sinA＜ cosB　　　C、sinA = cosB　　 D、以上都有可能

3、在△ABC中，sinA: sinB: sinC=(+1): (-1) :则最大角为　（　）

A、90⁰　　 B、120⁰　　　C、135⁰　　 D、150⁰

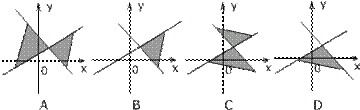
4.不等式 表示的平面区域是（　）

5、设x+3y –2 =0，则函数z=3^x+27^y +3的最小值是　（　 ）

A、3　　 B、3+2　　  C、6　　 D、9

6、已知x＞1，y＞1且lgx+lgy=4，则lgx·lgy的最大值是　 （　）

A、4　　 B、2　　　C、1　　 D、

7、设x＞0，y＞0且+=1，则xy有　　 (　　 )

A、最大值64　　 B、最小值　　  C、最小值　　 D、最小值64

8、.若则目标函数取值范围是（　）。

A [2,6]　　 B[2,5]　　C[3,6]　　　D[3,5]

9、不等式表示的平面区域包含点(0,0)和点(-1,-1)，则m的取值范围是(　 )。

A –3<m<3　 B 0<m<6　C –3<m<6　　 D 0<m<3

10、下列条件能判断△ABC一定为钝角三角形的是　（　 ）

①sinA + cosA= ②·＞0 ③ b=3, c=3, B=30⁰  ④tanA+ tanB+ tanC＞0

A、①④　　 B、①②　　　C、②③　　 D、③④

二、填空题(每题5分，合计20分)

11、若一个数不小于它的倒数，则这个数的取值范围是_{-----------------------}。

12、周长为L的矩形面积的最大值为_{-------- ---}，对角线长的最小值为_------------。

13已知函数z=x＋y，则z在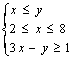的约束条件下的最大值是_________。

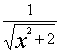
14、给出下列四个命题①x+2,（x＞0）　②+2,

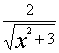③函数f(x)=sin+　∈(0, )时的最小值为2；④函数f(x)= +的最小值为2。其中正确的有_{--------------------}。

答题卡

1	2	3	4	5	6	7	8	9	10

11_{-------------------------------------------------------------}。　12_{------------------------------------------------------------}。　　　

13_{-------------------------------------------------------------}。　14_{-------------------------------------------------------------}。

三、解答题

15、已知f(x)=mx²-n且- 4f(1)-1, -1f(2)5,求f(3)的取值范围。

16、解不等式 ①（x²-9）（x²-3x-4）＞0　②1 ③<3请任选两题做。

17、在△ABC中，角A、B、C所对的边a、b、c，b =a cosC，又△ABC的最大边长为12，最小角的正弦为，（1）判断△ABC的形状；（2）求△ABC的面积。

18、江岸边有一炮台高30米，江中有两条船，由炮台顶部测得俯角分别是45⁰和30⁰，而且两条船与炮台底部连线成30⁰角，求两条船相距多少米？

19、m取何范围时，关于x的方程x²-2（m+2）x+m² –1=0 ①有两个正根②有一个正根，一个负根。

20、k为何值时，不等式0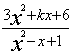＜6对任意实数x恒成立?

答案：

1	2	3	4	5	6	7	8	9	10
D	A	B	C	D	A	D	A	D	B

11-1a <0或a1　 12、，_（/4）L　 13、31　 14、①　　 15、[-1，20]

16、①x <-3或-1<x <3或x.>4　　 ②-2x<或x<　　　③x <-1或x.>

17、①直角三角形　 ② 18　　　　 18、10　

19① -m<-1或m>1　②-1<a <1　　　 20、k= - 6