《正弦定理、余弦定理、解斜三角形》第二课时
一、复习要求：
1、 掌握利用正弦定理及余弦定理解任意三角形的方法；
2、 会利用数学建模思想，解决生产实际中的问题；
3、 灵活用正、余弦定理及三角形面积公式解决有关问题。
二、典型例题分析；
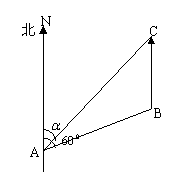例1：甲船在A处观测到乙船在它的北偏东600的方向，两船相距S海里，乙船正向北行驶，若甲船的速度是乙船的
倍，问甲船应取什么方向前进才能在最短的时间内追上乙船？此时乙船已行驶了多少海里？
解析：如图，设乙船的速度为V，则甲船的速度为
，
又设甲船以北偏东
角的方向行驶t时间后追上乙船，则
，
，
，
，于是在
中，应用余弦定理，
可得：
故 =600 -
300 =300 ，所以甲船应取北偏东300的方向行驶才能在最短的时间内追上乙船，此时乙船行驶了S海里。
练习1。灯塔A在灯塔B东偏南1500的方向，这两个灯塔相距20海里，从轮船K看见灯塔B在它的正南方，求轮船离这两个灯塔的距离。
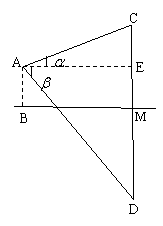
例2；在湖面上高h m处，测得云的仰角为a，而湖中云之影（即云在湖中的像）的俯角为
试证：云高为： 
解：画出图，设湖面上高h m处为A，测得云C的仰角为a，而云C在湖中的像D的俯角为，CD与湖面交于M，过A的水平线交CD于E，设云高CM=x，则CE=x-h,DE=x+h,AE=(x-h)cota, 又AE=（x+h）cot,
所以,(x-h)cota=(x+h)cot,
解得 
练习2：海岛0上有一座海拔1000米的山，山顶设有一个观测A，上午11时测得一轮船在岛600东的C处，俯角为300，11时10分又测得船在岛北600西的B处，俯角为600，（1）该船的速度为每小时多少千米？（2）若船以匀速继续航行，则它何时到达岛的正西方向？此时所在的点D离开海岛多少千米？
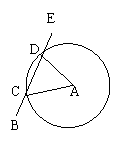例3：在气象台A正西方向300Km处有一台风中心，它以每小时40Km的速度向东北方向移动，距离台风中心250Km以内的地方都受其影响，问从现在起，大约多长时间后，气象台A所在地将遭受台风影响，持续多长时间？
解：如图，设台风从A的正西方向300Km处沿BE方向移动，
， 以A为圆心，250Km为半径画圆，交BE于C、D两点，设BC=x1,BD=x2
,由余弦定理可知，x1,
x2都满足方程
整理得 
解之得 
答：大约1.9小时后,A将遭受到台风影响,持续时间约为6.6小时.
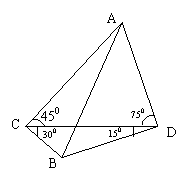
练习3：我炮兵阵地位于地面点A处，两观测所分别位于地面点C处和点D处，
已知CD=6000m 
目标出现于地面点B处时，测得
，如图，求炮兵阵地到目标的距离（结果保留根号）