江口中学2004—2005年高一数学复习题(附答案)
说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题),满分150分,考试时间100分钟.
姓名_______________班别___________座号_________得分_______
(收集设计:卓益声)
第Ⅰ卷(选择题,共60分)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将所选答案写在答题卡上)
1、设集合M = {x x2 < 4 }, N = {x![]() },则集合M ∩ N 等于( )。
},则集合M ∩ N 等于( )。
A.{![]() } B.{x x > 3} C. {
} B.{x x > 3} C. {![]() }
D.{
}
D.{![]() }
}
2、下列四个图像中,是函数图像的是( )。
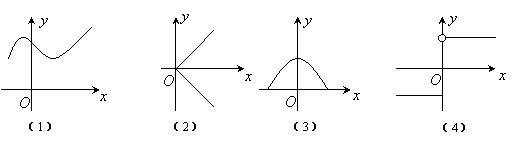 A.(1) B.(1)、(3)、(4)
C.(1)、(2)、(3) D.(3)、(4)
A.(1) B.(1)、(3)、(4)
C.(1)、(2)、(3) D.(3)、(4)
3、下列函数中,在![]() 上为减函数的是 ( )。
上为减函数的是 ( )。
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
![]()
 4、下面是属于正六棱锥的侧视图的是 ( )。
4、下面是属于正六棱锥的侧视图的是 ( )。
5、已知两个球的体积之比为1:8 ,则大球与小球的表面积之比为( )。
A.1:2 B.2 : 1 C.1:4 D.4:1
6、已知a = ![]() , b =
, b = ![]() , c =
, c = ![]() , 则a、b、c的大小关系是( )。
, 则a、b、c的大小关系是( )。
A.c>a>b B.c>b>a C.a>b>c D.b>a>c
7、已知a = ![]() ,那么
,那么![]() 用a表示是( )。
用a表示是( )。
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8、下列说法正确的是( )。
A.一条直线与一个平面平行,它就和这个平面内的所有直线平行;
B.如果一个平面内的无数条直线平行于另一个平面,那么这两个平面平行;
C.过空间一点有且只有一条直线和已知平面垂直;
D.若平面![]() 上有一条直线垂直于平面
上有一条直线垂直于平面![]() 的两条平行直线,则
的两条平行直线,则![]() 。
。
9、直线l过原点(0,0),且不过第三象限,那么l的倾斜角![]() 的范围是(
)。
的范围是(
)。
A.[0 o,90 o] B.[90 o,180 o]
C.[90 o,180 o )或![]() = 0 o
D.[90 o,135 o]
= 0 o
D.[90 o,135 o]
10、一条直线经过点P(1,2),且与两点A(2,3),B(4,-5)的距离相等,则直线l的方程是( )。
A.![]() B.
B. ![]() 或
或 ![]()
C.![]() D.
D.
![]() 或
或 ![]()
11、圆![]() 的圆心到直线
的圆心到直线![]() 的距离是( )。
的距离是( )。
A.1 B.![]() C.
C. ![]() D.2
D.2
12、点(1,-1,2)是空间直角坐标系中的一个点,则此点关于z轴的对称点的坐标为( )。
A.(-1,-1,-2) B.(1,1,2)
C.(1,-1,-2) D.(-1,1,2)
第Ⅱ卷(非选择题,共90分)
二、填空题(本大题共4小题,每小题4分,共16分;把答案填在答题卷中相应的横线上)
13、函数![]() 的单调递增区间是_______________________;
的单调递增区间是_______________________;
14、![]() 则
则![]() _________________________________;
_________________________________;
15、经过点(2,3),并且在两轴上的截距相等的直线方程是_____________________________________________________;
16、有以下说法:①
若直线![]() 与
与![]() 的斜率相等,则
的斜率相等,则![]() ∥
∥![]() ;②若直线
;②若直线![]() 与
与![]() 的斜率均不存在,则
的斜率均不存在,则![]() ∥
∥![]() ; ③ 两条直线的斜率互为负倒数,则两直线互相垂直; ④ 若直线
; ③ 两条直线的斜率互为负倒数,则两直线互相垂直; ④ 若直线![]() ⊥
⊥![]() ,则两直线的斜率互为负倒数;⑤ 斜率均不存在的两条直线不可能垂直,也不可能平行。其中说法错误的有____________________________________。
,则两直线的斜率互为负倒数;⑤ 斜率均不存在的两条直线不可能垂直,也不可能平行。其中说法错误的有____________________________________。
姓名_______________班别___________座号_________得分_______
一、 选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将所选答案写在下面的表格内)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题(本大题共4小题,每小题4分,共16分;把答案填在答题卷中相应的横线上)
13、________________________________________ 14、_____________________
15、_______________________________________ 16、____________________
三、解答题(本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.):
17、(本小题满分12分)求(I)中函数的定义域,计算(II)的值。
(I)![]() (II)
(II)![]()
18.(本小题满分12分)证明函数![]() 是奇函数,并且在
是奇函数,并且在![]() 上单调递增;
上单调递增;
19、(本小题满分12分) 直线![]() 与直线
与直线![]() 没有公共点,求实数m的值。
没有公共点,求实数m的值。
 20、(本小题满分12分)如图,棱锥V—ABC中,VO⊥平面ABC, O∈CD , VA=VB,AD=BD;证明:CD⊥AB且AC=BC 。
20、(本小题满分12分)如图,棱锥V—ABC中,VO⊥平面ABC, O∈CD , VA=VB,AD=BD;证明:CD⊥AB且AC=BC 。
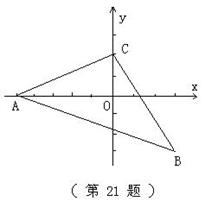 21、(本小题满分12分)如图,已知三角形的三个顶点A(-5,0),B(3,-3),C(0,2);求三角形ABC的面积。
21、(本小题满分12分)如图,已知三角形的三个顶点A(-5,0),B(3,-3),C(0,2);求三角形ABC的面积。
22、(本小题满分14分)22.(本小题满分14分)设函数![]() 是定义在
是定义在![]() 上的减函数,并且满足下面三个条件:(1)对任意正数
上的减函数,并且满足下面三个条件:(1)对任意正数![]() ,都有
,都有![]() ;(2)当
;(2)当![]() 时,
时,![]() ;(3)
;(3)![]() ,
,
(I)求![]() 、
、![]() 的值;
的值;
(II)如果不等式![]() 成立,求x的取值范围.
成立,求x的取值范围.
(III)如果存在正数k,使不等式![]() 有解,求正数
有解,求正数![]() 的取值范围.
的取值范围.
江口中学2004—2005年高一数学复习题(参考答案)
一、
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | B | C | A | C | A | A | C | C | B | B | D |
二、
13、( 1 , 2
] 14、 ![]()
15、![]() 16、 ①、 ④、 ⑤
16、 ①、 ④、 ⑤
三、
17、(本小题满分12分)求(I)中函数的定义域,计算(II)的值。
|
|
18.(本小题满分12分)证明函数![]() 是奇函数,并且在
是奇函数,并且在![]() 上单调递增;
上单调递增;
证明:
 19、(本小题满分12分) 直线
19、(本小题满分12分) 直线![]() 与直线
与直线![]() 没有公共点,求实数m的值。
没有公共点,求实数m的值。
解:①当m=0时,直线方程分别化成![]()
![]()
②当![]() 直线方程化成斜截式方程分别为
直线方程化成斜截式方程分别为![]() 和
和![]() ,两直线没有公共点,则
,两直线没有公共点,则![]() 并且
并且![]() ,解得,
,解得,![]()
综合①②得 m=0 或者 ![]() 。
。
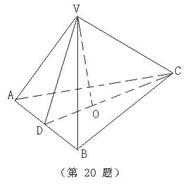 20、(本小题满分12分)如图,棱锥V—ABC中,VO⊥平面ABC, O∈CD , VA=VB,AD=BD;证明:CD⊥AB且AC=BC 。
20、(本小题满分12分)如图,棱锥V—ABC中,VO⊥平面ABC, O∈CD , VA=VB,AD=BD;证明:CD⊥AB且AC=BC 。
证:
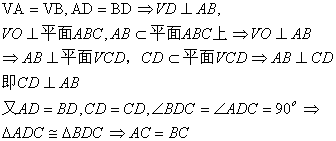
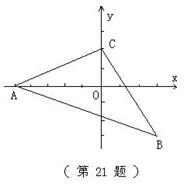 21、(本小题满分12分)如图,已知三角形的三个顶点A(-5,0),B(3,-3),C(0,2);求三角形ABC的面积。
21、(本小题满分12分)如图,已知三角形的三个顶点A(-5,0),B(3,-3),C(0,2);求三角形ABC的面积。
解:

22、(本小题满分14分)22.(本小题满分14分)设函数![]() 是定义在
是定义在![]() 上的函数,并且满足下面三个条件:(1)对任意正数
上的函数,并且满足下面三个条件:(1)对任意正数![]() ,都有
,都有![]() ;(2)当
;(2)当![]() 时,
时,![]() ;(3)
;(3)![]() ,
,
(I)求![]() 、
、![]() 的值; (II)如果不等式
的值; (II)如果不等式![]() 成立,求x的取值范围.
成立,求x的取值范围.
(III)如果存在正数k,使不等式![]() 有解,求正数
有解,求正数![]() 的取值范围.
的取值范围.
解:(I)令![]() 易得
易得![]() .而
.而![]()
且![]() ,得
,得![]() .
.
(II)由条件(1)及(I)的结果得:![]() 其中
其中![]() ,由函数
,由函数![]() 在
在![]() 上的递减性,可得:
上的递减性,可得: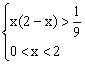 ,由此解得x的范围是
,由此解得x的范围是![]() .
.
(III)同上理,不等式![]() 可化为
可化为![]() 且
且![]() ,
,
|
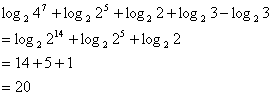 .
.