高一数学下末综合练习（二）
姓名 班级 得分
一、选择题 (本大题共12个小题，每小题5分，共60分)
1、满足条件
1的范围是 (以下
)
( C )
A．
B．
C．
D． 
2、已知α、β都是钝角，且
，
，那么
的值是
A．
B．
C．
D．或
3、函数
的值域是
A．
B．
C．
D．
4、若
，
,则x等于
A．
B．
C．
D． 
5、若
,则函数
的最小值是
A．
B．
C．0 D．1
6、已知
,则
的值是
A．
B．
C．
D． 
7、若a=(1,3)，b=(-2,-1),则(3a+2b)(2a+5b)等于
A．
B．55 C．15 D．205
8、若a=(λ,2)，b=(-3,5),则a与b的夹角为钝角，则λ的取值范围是
A．
B．
C．
D． 
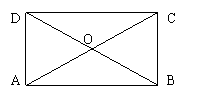9、在矩形ABCD中，
，
则
等于（ ）
A．
B．
C．
D．—
10、根据下列条件，确定ΔABC有两解的是 （ ）
A．a=18,b=20,A=120°; B．a=60,c=48,B=60°
C．a=3,b=6,A=30° D．a=14,b=16,A=45°
11、已知
，
，a与b的夹角为60°，又c=ma+3b,d=2a-mb，且c⊥d，则m的值是 ( )
A．0 B．1或—6 C．—1或6 D．—6或6
12、在ΔABC中，
，
，
，下列推导不正确的是（ ）
A．若a·b<0，则ΔABC为锐角三角形 B．a·b=0, 则ΔABC为直角三角形 C．a·b= b·c, 则ΔABC为等腰三角形 D．c·（a+b+c）=0, 则ΔABC为正三角形
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题 (本大题共四个小题，每小题5分，共20分)
13、已知，，a与b的夹角为
，则向量2a+3b与3a-b的夹角（可用反三角函数表示）____________
14、函数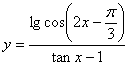
的定义域是____________
15、
+
—
=____________
16、平面内三点A、B、C在一条直线上，
，
，
且
⊥
，（m,n∈N）则m+n=____________
三、解答题 (本大题共6个小题，共70分)
17、已知函数
，
，那么
（1） 函数的最小正周期是什么？
（2） 函数在什么区间上是增函数？
（3） 函数的图象可以由函数
，的图象经过怎样的变换得到？
18、已知向量a、b、c两两所成的角相等，并且，
，
，
（1） 求向量a+b+c的长度；（2）向量a+b+c与a、b、c的夹角
19、已知
，
，
成等差数列，，
，成等比数列，求
的值
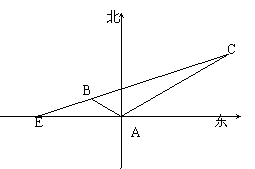20、如图,某海岛上一观察哨所A上午11时测得以轮船在海岛北偏东
的C处,12时20分时测得船在海岛北偏西的B处,12时40分轮船到达位于海岛正西方且距海岛5km的E港口，如果轮船始终保持匀速直线运动，问船速是多少？
21、平面内有向量
，
，
，点X为直线OP上一动点.
(1)
当
取最小值时，求的
坐标；
(2) 当点X满足（1）的条件和结论时，求cos∠AXB的值
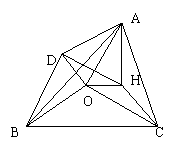
22、如图，设ΔABC的外心为O，以线段OA，OB为邻边作平行四边形，第四个顶点为D，再以OC与OD为邻边作平行四边形，它的第四个顶点为H，
（1）
若
，
，
，
，用a、b、c表示h；
（2） 证明AH⊥BC；
（3） 设ΔABC的中，∠A=60°，∠B=45°，外接圆半径为R，用R表示h
 |
高一数学综合练习（二）(答案)
一选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | A | D | C | C | D | C | A | A | D | B | D |
二、填空题
13、
；14、
；15、0；16、9；
17、解：函数=
,函数的最小正周期是π，
18、分两种情况：当向量a、b、c两两所成的角为
时,
, a+b+c与a、b、c的夹角为;当向量a、b、c两两所成的角为
时，
=
=
=12, 
=
,
,同理
=0，
，
，
19、解：由条件得2=+ 
=
故
=1+2
,
解得
，由于
，所以
，故，
，
，
20、［解］轮船从C处到点B耗时80分钟，从点B处到点E耗20分钟, 轮船保持匀速直线运动∴BC=4EB,设BE＝x,BC=4x,由已知得只要求出
的值即可在△AEC中
sinC=
在△ABC中AB=
=
在△ABE中,由余弦定理
=
,∴BE=
∴轮船船速是
(km/t)
21、解：（1）设=（x,y）,∵点X为直线OP上,∴与
共线，又
∴x×1—y×2=0
即 x=2y, =（2y,y）, 又
,,∴
,同理
=
，于是=
=
，当y=2,时，有最小值-8，此时=（4，2）；（2）当=（4，2），即y=2,时，有
，
，
，= —8，∴cos∠AXB=
22、（1）由向量加法的平行四边形法则，得
，
=a+b+c，∴h= a+b+c；（2）
，∴
=
，∵O为ΔABC的外心，∴
即
，∴
⊥
，AH⊥BC；（3）在ΔABC的中，∠A=60°，
∠B=45°，则∠BOC=2∠A=120°，∠AOC=2∠B=90°，∠AOB=150°，外接圆半径为R，
==
=
++—
+0—=
，
=