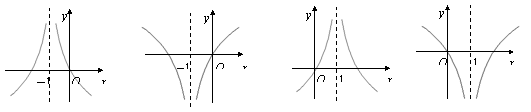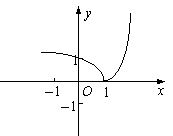试卷类型：A
襄樊市高中调研测试题(2004.12)
高 一 数 学
一．选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1. 满足{2}ÍMÜ{1，2，3}的集合M有
A．2个 B．3个 C．4个 D．5个
2. 
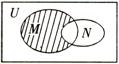如图，U为全集，M，N是集合U的子集，则阴影部分所表示的集合是
A．M∩N B．∁U (M∩N)
C．(∁U M)∩N D．(∁U N)∩M
3.
函数y＝5x＋1 (x∈R)的反函数是
A．
B．
C．
D．
4.
若x，a，2x，b成等比数列，则
的值为
A．
B．
C．2 D．
5.
函数
的单调递减区间为
A．[3，4) B．(2，3] C．[3，＋∞) D．[2，3]
6.
b2＝ac是a，b，c成等比数列的
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分又不必要条件
7.
若p是真命题，q是假命题，则①p且q；②p或q；③非p；④非q．四个命题中假命题的个数是
A．1 B．2 C．3 D．4
8.
已知等比数列{an}的公比为
，则
A．
B．16 C． D．2
9.
等差数列{an}的前n项和为Sn，已知a1＜0，公差d＞0，S6＝S11，下述结论中正确的是
A．S10最小 B．S9最大 C．S8，S9最小 D．S8，S9最大
10. 某公司今年初向银行贷款a万元，年利率为q（复利计息），从今年末开始每年末偿还相同的金额，预计五年内还清，则每年末应偿还的金额是
A．
万元 B．
万元
C．
万元 D．
万元
11. 已知函数y＝f (x)的图象关于直线x＝－1对称，当x∈(0，＋∞)时，
，则当x∈(－∞，－2)时，f (x)的解析式是
A．
B．
C．
D．
|
|
12. 函数
的图象大致是
A B C D
二．填空题：本大题共4小题，每小题4分，共16分。将正确答案填在题中横线上．
13.
数列{an}中，a1＝1，a2＝2，
(n≥2，n∈N*)，则这个数列的前10项和为
．
14.
已知函数
，若
，则x＝ ．
15. 数列{an}中，a1＝2，an＋1－an＝3n (n∈N*)，则数列{an}的通项为an＝ ．
16.
老师给出一个函数
，四个学生各指出这个函数的一个性质：
甲：对于x∈R，都有
；
乙：在(－∞，0]上函数递减；
丙：在[0，＋∞)上函数递增；
丁：f (0)不是函数的最小值。
如果其中恰有三人说的正确，请写出这样的一个函数
．
三．解答题：本大题共6小题，满分74分．
|
|
17. (本大题满分12分) 已知函数
(1)作出其图像；
(2)由图像指出函数的单调区间；
(3)由图像指出当x取何值时，函数有最值，并求出最值．
18.
(本大题满分12分) 已知集合A＝{x êx2＋(a－1)x－a＞0}，B＝{x ê(x＋a)(x＋b)＞0}，其中a≠b，M＝{x êx2－2x－3≤0}，全集U＝R．
(1)若∁UB＝M，求a、b的值；
(2)若a＞b＞－1，求A∩B；
(3)若a2＋
∈∁UA，求a的取值范围．
19、(本大题满分12分) 某工厂生产的一种产品，原计划今年第一季度的产量逐月增加相同的件数，但实际生产中，2月份比原计划多生产了10件，3月份比原计划多生产了25件，这样三个月的产量恰成等比数列，并且第三个月的产量只比原计划第一季度总产量的一半少10件．问这个厂第一季度共生产了多少件这种产品？
20、(本大题满分12分) 已知等差数列{an}中，a1＝2，a1＋a2＋a3＝12．
(1)求数列{an}的通项公式；
(2)令bn＝anxn (x∈R)，求数列{bn}的前n项和．
襄樊市高中调研测试题(2004．12)
高一数学参考答案及评分标准
说明：
1．本解答指出了每道题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．
2．对计算题当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定给分，但不得超过该部分正确解答应得分数的一半；如果后续部分的解答有较严重的错误，就不再给分．
3．解答右端所注分数，表示考生正确做到这一步应得的累加分数．
4．只给整数分数，选择题和填空题不给中间分数．
一．选择题：BDDAB BBBCC CD
二．填空题：13．210－1 14． 15．
16．f (x)＝(x－1)2
三．解答题
|
|
17．(1)解：函数可化为
4分
图象如图． 6分
(2)解：由图象可以看出，函数的单调递减区间是
(－∞，1]，单调递增区间是[1，＋∞)． 10分
(3)解：由图象可以看出，当x＝1时函数有最小值，且最小值为0． 12分
18．(1)解：A＝{x ê(x－1)(x＋a)＞0}，M＝{x ê－1≤x≤3}
∁UB＝{x｜(x＋a)(x＋b)≤0}
若∁UB＝M，则a＝1，b＝－3或a＝－3，b＝1． 4分
(2)解：∵a＞b＞－1 ，∴－a＜－b＜1
故A＝{x êx＜－a或x＞1}，B＝{x êx＜－a或x＞－b}
因此A∩B＝{x êx＜－a或x＞1}． 6分
(3)∁UA＝{x ê(x－1)(x＋a)≤0}，
由a2＋
∈∁UA 得：(a2－
)( a2＋＋a)≤0， 8分
解得：
或
，
∴a的取值范围是{x｜或}． 12分
19．解：依题意，原计划每月的产量成等差数列，设为a－d，a，a＋d (d＞0) 4分
由已知得：a－d， a＋10，a＋d＋25成等比数列 6分
∴
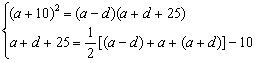8分
解得：a＝90，d＝10 10分
∴第一季度共生产了(90－10)＋(90＋10)＋(90＋10＋25)＝305件这种产品． 12分
20．(1)解：设公差为d，由a1＋a2＋a3＝12 得 3a1＋3d＝12，解得d＝2
∴数列的通项公式为 an＝2n (n∈N*)． 4分
(2)解：∵bn＝anxn
∴Sn＝2x＋4x2＋6x3＋…＋(2n－2)xn－1＋2nxn 6分
＝2x[1＋2x＋3x2＋4x3＋…＋(n－1) xn－2＋nxn－1
] ①
xSn＝2x[x＋2x2＋3x3＋4x4＋…＋(n－1) xn－1＋nxn ] ②
①－②得：(1－x)Sn＝2x[1＋x＋x2＋x3＋…＋xn－1 －nxn ] 8分
当x≠1时，
10分
当x＝1时，Sn＝2＋4＋6＋…＋2n＝n(n＋1) 12分
21．(1)由(an＋1－an)(4an－4)＋(an－1)2＝0得 (an－1)(4an＋1－3 an－1)＝0
∵a1＝2，∴an－1＝0不可能对一切n∈N*成立
∴4an＋1－3 an－1＝0，得 
4分
(2)证：∵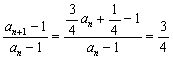
∴数列{ an－1}是等比数列． 6分
(3)解：由(2)知，
∴
8分
于是
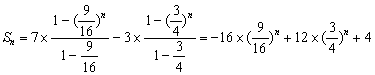
10分
由于
对n∈N*不成立，故考虑使
接近于
的正整数n
当n＝1时，
，n＝2时，
，n＝3时，
，n＝4时，
，由于
，∴当n＝3时，(Sn)max＝
即数列{Sn}的最大值为
． 12分
22．(1)解：由已知得：
∴
(2)证：设
，则
∵
≤0，
＜0
两式相加得：
＜0，即
＜0
∴f (x1)－f (x2)＜0，即f (x1)＜f (x2)
∴f (x)在[
]上的是增函数．
(3)解：由(2)知，f (x)在[]上的最小值、最大值分别为
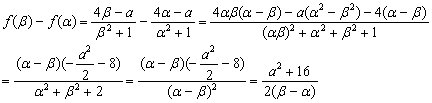
又
∴
≥4，此时a＝0
∴当a＝0时，f (x)在区间[]上的最大值与最小值之差最小．
21、(本大题满分12分) 已知f (x)＝(x－1)2，g (x)＝4x－4，数列{an}满足a1＝2，(an＋1－an)g(an)＋f (an)＝0
(n∈N*)．
(1)用an表示an＋1；
(2)证明数列{ an－1}是等比数列；
(3)设bn＝7f (an)－g (an＋1)，Sn是数列{bn}的前n项和，试求数列{Sn}中的最大项．
22、(本大题满分14分)设关于x的一元二次函数2x2－ax－2＝0的两个根为
(
)，函数
．
(1)求
；
(2)证明f (x)是[]上的增函数；
(3)当a取何值时，f (x)在区间[]上的最大值与最小值之差最小．