平面向量的坐标表示
【基础知识精讲】
1.平面向量的坐标表示：在平面直角坐标系内，分别取与x轴、y轴正方向相同的两个单位向量
、
作为基底，对任一向量
，由平面向量基本定理知，有且只有一对实数(x,y)，使得=x+y,则实数对(x,y)叫做向量的直角坐标(简称坐标)，记作=(x,y)，其中x和y分别称为向量的x轴上的坐标与y轴上的坐标，而=(x,y)称为向量的坐标表示.
相等的向量其坐标相同.同样，坐标相同的向量是相等的向量.
显然=(1,0), =(0,1), 
=(0,0)
2.平面向量的坐标运算：
(1)两个向量和与差的坐标分别等于这两个向量相应坐标的和与差：
±
=(x1±x2,y1±y2)(其中=(x1,y2)、=(x2,y2)).
(2)一个向量的坐标等于表示此向量的有向线段的终点的坐标减去始点的坐标.
如果A(x1，y1)、(x2,y2)，则
=(x1-x2,y1-y2)
(3)实数与向量的积的坐标等于用这个实数乘以原来向量的相应坐标.
若=(x,y),则λ=(λx,λy)
3.向量平行的坐标表示
已知向量、(≠)，则∥的充要条件为存在实数λ，使=λ.
如果=(x1,y1), =(x2,y2)( ≠)则∥的充要条件为：x1y2-x2y1=0.
平面向量的坐标表示，实际是向量的代数表示，此入向量的坐标表示以后，可以使向量运算完全代数化，将数与形紧密地结合起来，这样很多的几何问题的证明，就可以转化为学生熟悉的数量的运算.
两个向量相加减，是这两个向量的对应坐标相加减，这个结论可以推广到有限个向量相加减.
【重点难点解析】
1.向量的坐标与表示该向量的有向线段的起始点的具体位置没有关系，只与其相对位置有关系，即两个向量不论它们的起始点坐标是否相同，只要这两个向量的坐标相同，那么它们就是相等向量.
两个向量如果是相等的，那么它们的坐标也应该是相同的.
2.向量的坐标是终点的坐标减去始点的对应坐标，而不是始点的坐标减去终点的坐标.
3.实数λ与向量的积的运算时，λ应与的相应坐标相乘，以下的结论都是错误的.
设λ∈R，=(x,y)
λ=λ(x,y)=(λx,y)
或λ=λ(x,y)=(x,λy)
例1
若向量=(x+3,x2-3x-4)与相等，其中A(1，2)，B(3，2)，则x=
例2
已知=(3x+4y,-2x-y), =(2x-3y+1,-3x+
y+3)，若2=3,试求x与y的值.
例3 已知平行四边形三个顶点是(3，-2)，(5，2)，(-1，4)，求第四个顶点的坐标.
解：如图，设
=(3,-2), 
=(5,-2), 
=(-1,4), 
=(x,y)
依题意，=
或
=
或=
由=，可得：-=-
即(5,2)-(3,2)=(-1,4)-(x,y) 
(2,4)=(-1-x,4-y)
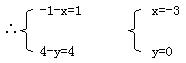
∴D(-3，0)
同理，若=可得：(-4，6)=(5-x,2-y).
∴x=9,y=-4, ∴D(9,-4)
若=可得：(2，4)=(x+1,y-4)
∴x=1,y=8. ∴D(1,8)
∴点D的坐标为(-3，0)或(9，-4)或(1，8)
例4
已知｜｜=10, =(3,-4),且∥,求.
例5
已知=(3,2), =(-2,1), 
=(7,-4),用，表示.
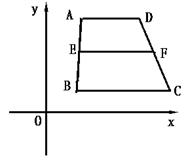
例6
如图，已知凸四边形ABCD中，E、F分别是AB与CD的中点，试证：2
=
+
【难题巧解点拔】
例1 已知：点A(2，3)、B(5，4)，C(7，10)
若
=+λ· (λ∈R),试求λ为何值时，点P在一、三象限角平分线上?点P在第三象限内?
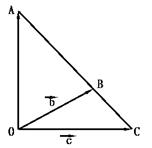
例2
如图已知=,=, =,求证A、B、C三点在一条直线上的充要条件是：有不全为0的实数m,n,l，使得l+m+n=0且l+m+n=0
【典型热点考题】
例1
若向量=(1,2), =(x,1), 
=+2,
=2-,且∥，则x= .
解：=(1,2)+2(x,1)=(1,2)+(2x,2)=(2x+1,4)
=2(1,2)-(x,1)=(2,4)-(x,1)=(2-x,3)
由∥,一定存在λ∈R，使=λ
则有(2x+1,4)=((2-x)λ,3λ)
解得：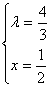
∴应填
.
例2
若点A(-1，2)，B(2，3)，C(3，-1)，且=2-3，则点D的坐标为 .
例3
若A、B、C三点的坐标分别为(2，-4)，(0，6)，(-8，10)，则+2，-的坐标分别为 、 .
例4
已知≠，≠, 不平行于,求证：+不平行于-.