三角单元测试·练习题
一、选择题((1)题~(10)题每小题4分,(11)题~(15)题每小题5分,共65分)
![]()
[ ]
A.第一象限 B.第二象限
C.第三象限 D.第四象限
![]()
[ ]
A.-2 B.-1
C.1 D.2
(3)如果sinxsiny=1,那么2cos(x+y)的值等于 [ ]
A.-2 B.0
C.2 D.±2
![]()
[ ]

(5)函数f(x)=sin2x-cos2x的最小正周期是 [ ]
![]()
C.2π D.4π
![]()
[ ]
A.[0,2] B.[0,2)
C.(0, 2] D.(0,2)
![]()
[ ]
A.奇函数非偶函数
B.偶函数非奇函数
C.非奇非偶函数
D.既是奇函数又是偶函数
![]()
[ ]
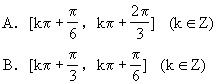
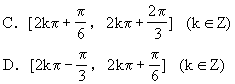
(9)下列函数中,周期为π的函数是 [ ]
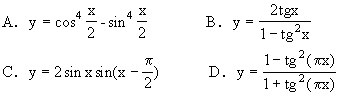
![]()
![]()
[ ]

(11)已知点M(sinθ-cosθ,tgθ)在第一象限,则在[0,2π)内θ的取值范围是 [ ]


![]()
[ ]

(13)在斜三角形ABC中,若sinA=cosBcosC,那么下列四式的值必为常数的是 [ ]
A.sinB+sinC B.cosB+cosC
C.tgB+tgC D.ctgB+ctgC
(14)一个直角三角形三内角的正弦值成等比数列,其最小内角为
[ ]

(15)将函数y=f(x)图象上每一点的纵坐标保持不变,横坐标扩大到原
![]()
y=3sinx的图象相同,则函数y=f(x)的表达式是 [ ]
![]()
C.f(x)=-3sin2x D.f(x)=-3cos2x
二、填空题(每小题4分,共16分)
![]()
(17)函数f(x)=sinxcos2α-cosxsin2α的图象关于y轴对称,则α=______.
(18)函数f(x)=11-8cosx-2sin2x的最大值是______.
![]()
①由f(x1)=f(x2)=0,可得x1-x2=kπ(k∈Z)

其中正确命题的序号是______.
三、解答题(本题有6小题,共69分)
(20)(10分)已知角α的顶点与直角坐标系的原点重合,始边在x轴的
![]()


(23)(12分)求函数y=(sin3xsin3x+cos3xcos3x)·see22x+sin2x的最小值.
(24)(12分)在△ABC中,a,b,c分别是内角A,B,C的对边,
![]()
(25)(12分)已知△ABC中,三个内角A,B,C成等差数列,cosB
![]()
答案与提示
一、
| (1)D | (2)D | (3)A | (4)D | (5)B | (6)B | (7)A | (8)A |
| (9)C | (10)C | (11)B | (12)B | (13)C | (14)B | (15)D |
|
提示

![]()
(3)∵sinx≤1,siny≤1,由sinxsiny=1知sinx=1,siny=1或sinx=-1,siny=-1
当sinx=siny=1时,cosx=cosy=0,此时2cos(x+y)=2(cosxcosy-sinxsiny)=-2
当sinx=siny=-1时,cosx=cosy=0,2cos(x+y)=-2

![]()
![]()
(7)y=sin2x是奇函数,不是偶函数.


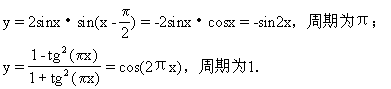
∴选C.
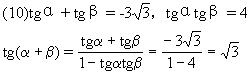

(11)点M(sinθ-cosθ,tgθ)在第一象限,
∴sinθ-cosθ>0,且tgθ>0
即sinθ>cosθ,且tgθ>0又θ∈[0,2π)

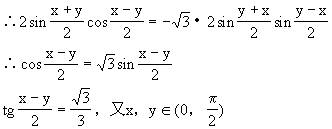

∵sinA=cosBcosC ∴tgB+tgC=1(常数)
(14)设Rt△ABC中,∠C=90°,A<B
依题意有:sinA,sinB,sinC成等比数列,则sin2B=sinAsinC=sinA
又sinB=cosA ∴sinA=cos2A=1-sin2A
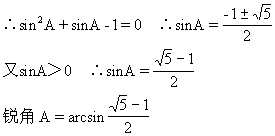
(15)把 f(x)=-3cos2x纵坐标不变,横坐标扩大到原来的2倍,得函数



提示

∴sin3θ+cos3θ=(sinθ+cosθ)(1-sinθcosθ)
![]()
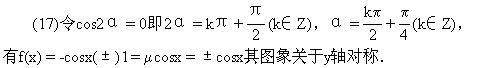
(18)y=11-8cosx-2sin2x=2(cosx-2)2+1,cosx≤1,当cosx=-1时,ymax=19
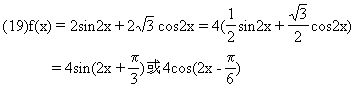
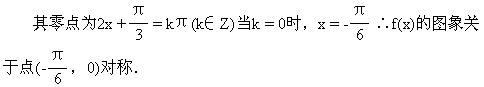

![]()

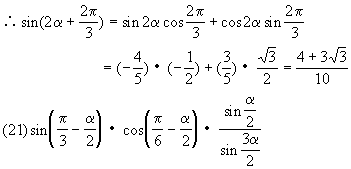


![]()
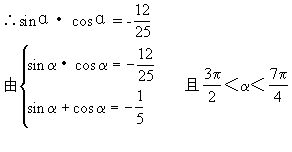
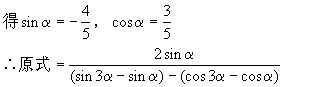
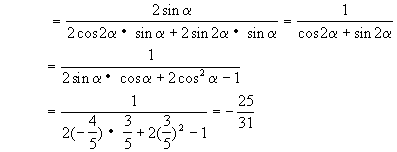
(23)y=(sin3x·sinx·sin2x+cos3x·cosx·cos2x)·sec22x+sin2x
=[sin3x·sinx(1-cos2x)+cos3x·cosx·cos2x]·sec22x+sin2x
=[sin3x·sinx+cos2x(cos3x·cosx-sin3x·sinx)]·sec22x+sin2x



(24)∵a,b,c成等差数列,∴a+c=2b即
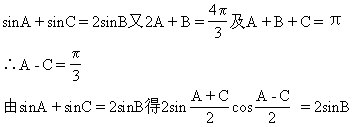

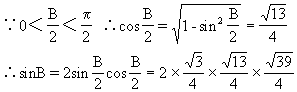
(25)∵A,B,C成等差数列,又A+B+C=π
![]()