函数的性质、反函数·函数的单调性·例题
例1-5-1 下列函数中,属于增函数的是 [ ]
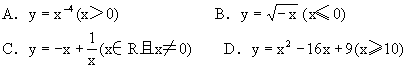
解 D
例1-5-2 若一次函数y=kx+b(k≠0)在(-∞,+∞)上是单调递减函数,则点(k,b)在直角坐标平面的 [ ]
A.上半平面 B.下半平面
C.左半平面 D.右半平面
解 C 因为k<0,b∈R.
例1-5-3 函数f(x)=x2+2(a-1)x+2在区间(-∞,4)上是减函数,则实数a的取值范围是 [ ]
A.a≥3 B.a≤-3
C.a≤5 D.a=-3
解 B 因抛物线开口向上,对称轴方程为x=1-a,所以1-a≥4,即a≤-3.
例1-5-4 已知f(x)=8+2x-x2,如果g(x)=f(2-x2),那么g(x)
[ ]
A.在区间(-1,0)内是减函数
B.在区间(0,1)内是减函数
C.在区间(-2,0)内是增函数
D.在区间(0,2)内是增函数
解 A g(x)=-(x2-1)2+9.画出草图可知g(x)在(-1,0)上是减函数.
![]()
+bx在(0,+∞)上是______函数(选填“增”或“减”).
![]()
![]()
解 [-2,1]
已知函数的定义域是-5≤x≤1.设
u=-x2-4x+5=-(x+2)2+9
可知当x∈[-5,-2]时,随x增大时,u也增大但y值减小;当x∈[-2,1]时,随x增大时,u减小,但y值增大,此时y是x的单调增函数,即
![]()
注 在求函数单调区间时,应先求函数的定义域.
例1-5-7 y=f(x)在定义域上是单调递增函数,且f(x)>0,那么在同
![]()
函数;y=[f(x)]2是单调______函数.
解 递减;递减;递增.
例1-5-8 (1)证明函数f(x)=x2-1在(-∞,0)上是减函数;
![]()
解 (1)任取x1<x2<0,则
![]()
所以 f(x1)>f(x2).
故f(x)在(-∞,0)上递减.
(2)任取0<x1<x2,则
![]()
当x2>x1>1时,f(x2)>f(x1);当1>x2>x1>0时,f(x2)<f(x1).
所以函数在(0,1]上是减函数,在[1,+∞)上是增函数.
例1-5-9 已知f(x)=-x3-x+1(x∈R),证明y=f(x)是定义域上的减函数,且满足等式f(x)=0的实数值x至多只有一个.
解 设x1,x2∈R,且x1<x2,则
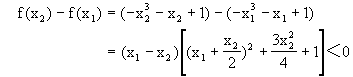
所以f(x1)>f(x2).所以y=f(x)是R上的减函数.
假设使f(x)=0成立的x的值有两个,设为x1,x2,且x1<x2,则
f(x1)=f(x2)=0
但因f(x)为R上的减数,故有f(x1)>f(x2).矛盾.所以使f(x)=0成立的x的值至多有一个.
例1-5-10 定义域为R的函数y=f(x),对任意x∈R,都有f(a+x)=f(a-x),其中a为常数.又知x∈(a,+∞)时,该函数为减函数,判断当x∈(-∞,a)时,函数y=f(x)的单调状况,证明自己的结论.
解 当x∈(-∞,a)时,函数是增函数.
设x1<x2<a,则2a-x1>2a-x2>a.
因为函数y=f(x)在(a,+∞)上是减函数,所以
f(2a-x1)<f(2a-x2)
注意到对任意x∈R,都有f(a+x)=f(a-x),可见对于实数a-x1,也有f[a+(a-x1)]=f[a-(a-x1)],即f(2a-x1)=f(x1).
同理f(2a-x2)=f(x2).
所以f(x1)<f(x2),所以函数y=f(x)在(-∞,a)上是增函数.
例1-5-11 设f(x)是定义在R+上的递增函数,且
f(xy)=f(x)+f(y)
![]()
(2)若f(3)=1,且f(a)>f(a-1)+2,求a的取值范围.
![]()
![]()
(2)因为f(3)=1,f(9)=f(3)+f(3)=2,于是
![]()
![]()
由题设有
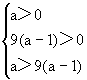
![]()