2.4 反函数·例题解析
【例1】求下列函数的反函数:
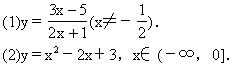
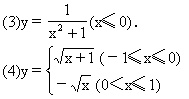
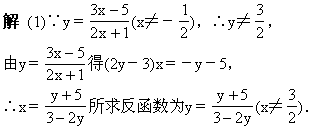
解 (2)∵y=(x-1)2+2,x∈(-∞,0]其值域为y∈[2,+∞),
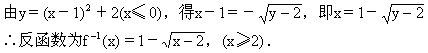
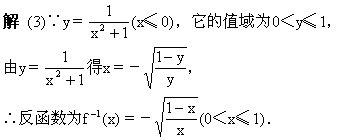
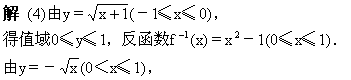
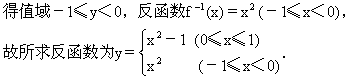
【例2】求出下列函数的反函数,并画出原函数和其反函数的图像.
![]()
解 (1)∵已知函数的定义域是x≥1,∴值域为y≥-1,
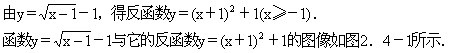
解 (2)由y=-3x2-2(x≤0)得值域y≤-2,
![]()
它们的图像如图2.4-2所示.
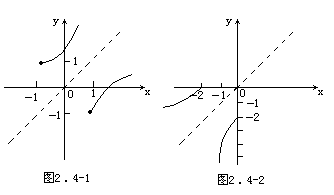
![]()
(1)求它的反函数;(2)求使f-1(x)=f(x)的实数a的值.
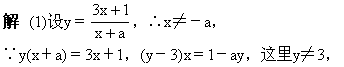

![]()
令x=0,∴a=-3.
或解 由f(x)=f-1(x),那么函数f(x)与f-1(x)的定义域和值域相同,定义域是{xx≠a,x∈R},值域y∈{yy≠3,y∈R},∴-a=3即a=-3.
![]()
试求a、b、c、d满足什么条件时,它的反函数仍是自身.
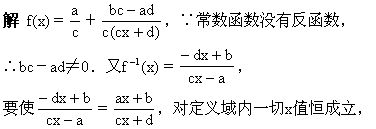
令x=0,得-a=d,即a+d=0.
事实上,当a+d=0时,必有f-1(x)=f(x),
因此所求的条件是bc-ad≠0,且a+d=0.
【例5】设点M(1,2)既在函数f(x)=ax2+b(x≥0)的图像上,又在它的反函数图像上,(1)求f-1(x),(2)证明f-1(x)在其定义域内是减函数.


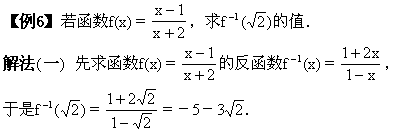
解法(二) 由函数y=f(x)与其反函数y=f-1(x)之间的一一对应关
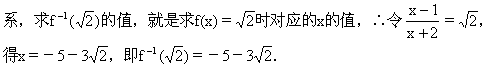


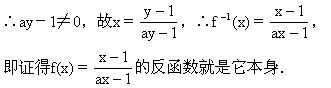
因为原函数的图像与其反函数的图像关于直线y=x对称,
∴函数y=f(x)的图像关于直线y=x对称.