交集、并集·基础练习

交集、并集·基础练习

 

(一)选择题

1．已知I={x∈Nx≤7}，集合A={3，5，7}，集合B={2，3，4，5}，则

[　　]

A．C_IA={1，2，4，6}

B．(C_IA)∩(C_IB)={1，2，3，4，6}

D．B∩C_IA={2，4}

2．两个非空集合A、B满足A∩B=A且A∪B=A，那么A、B的关系是

[　　]

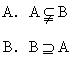
C．A=B

D．以上说法都不对

3．若4∩B={a，b}，A∪B={a，b，c，d}，则符合条件的不同的集合A、B有

[　　]

A．16对	B． 8对
C． 4对	D． 3对

4．已知集合A∪B={a，b，c，d}，A={a，b}则集合B的子集最多可能有

[　　]

A．8个	B．16个
C．4个	D．2个

5．已知集合A为全集I的任一子集，则下列关系正确的是

[　　]

(二)填空题

(1)A∩C_IA=________

(2)A∪C_IA=________

(3)A∩C_IB=________

(4)B∪C_IA=________

(5)C_II=________

(7)C_I(C_I(A∩B))=________

(8)A∩I=________

(9)B∪I=________

2．集合A={有外接圆的平行四边形}，B={有内切圆的平行四边形}，则A∩B=________．

3．设集合A={(x，y)a₁x＋b₁y＋c₁=0}，B={(x，y)a₂x＋b₂y＋

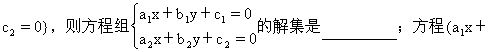
b₁y＋c₁)(a₂x＋b₂y＋c₂)=0的解集是________．

4．集合A={xx＜－2，或x＞2}，B={xx＜1，或x＞4}，则A∩B=________；A∪B=________．

实数a的取值范围是________．

(三)解答题

1．A={(x，y)ax－y²＋b=0}，B={(x，y)x²－ay－b=0}，已知

2．已知 A={xa≤x≤a＋3}，B={xx＜－1或x＞5}，

(2)若A∪B=B，求 a的取值范围．

3．设方程2x²＋x＋p=0的解集为A，方程2x²＋qx＋2=0的解

4．以实数为元素的两个集合A={2，4，a³－2a²－a＋7}，B={－4，a＋3，a²－2a＋2，a³＋a²＋3a＋7}，已知A∩B={2，5}，求：a．

5．某中学高中一年级学生参加数学小组的有45人，参加物理小组的有37人，其中同时参加数学小组和物理小组的有15人，数学小组和物理小组都没有参加的有127人，问该校高中一年级共有多少学生？

参考答案

(一)选择题</PGN0177B.TXT/PGN>

1．D(N={0，1，2，3，…}，而集合N中含有0是容易忽略的，故(A)C_IA={0，1，2，4，6}．(B)中(C_IA)∩(C_IB)=C_I(A∪B)={0，1，6}　(C)A∩C_IB只要找出在A中且不在B中的元素即可为{7})

2．C(根据集合运算的结果确定集合之间的关系是常用知识，由A

3．C(由韦恩图可推断如下：

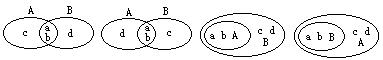
</PGN0178A.TXT/PGN>

4．B(B的元素个数n最多时子集个数最多，而集合B最多有4个元素为a、b、c、d，因此共有2⁴=16个子集．)

5．B(注意A为全集I的任一子集意味着A有可能是空集也有可能

(二)填空题

2．{正方形}(有外接圆的平行四边形可证明是长方形，有内切圆的平行四边形可证明是菱形)

3．A∩B；A∪B(注意“{”联立起来的方程组表示两个条件必须同时满足是“并且”的意思，而方程(a₁x＋b₁y＋c₁)(a₂x＋b₂y＋c₂)=0是a₁x＋b₁y＋c₁=0或a₂x＋b₂y＋c₂=0．)

4．(－∞，－2)∪(4，＋∞)；(－∞，1)∪(2，＋∞)

(A∩B：A∪B：)

(三)解答题

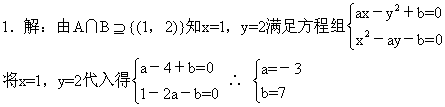
2．(1)解：

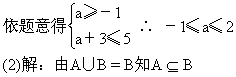
∴　a＋3＜－1或a＞5

∴　a＜－4或a＞5

4．解：∵　A∩B={2，5}

∴　5∈A代入得a³－2a²－a＋7=5</PGN0178B.TXT/PGN>

∴　a=2或a=±1

1)当a=2时，B={－4，5，2，25}　A={2，4，5}

2)当a=1时，B={－4，4，1，12}，与A∩B={2，5}矛盾，舍去

3)当a=－1时，同理舍去

∴　a=2

5．解：

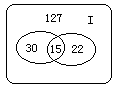
30＋15＋22＋127=194(人)答：该校高一年级学生共194人